文本局部敏感哈希-MinHash算法原理

Posted 2022-04-15 普通网友

  　最近在思考大量文本判重的问题，由于文本数据量大，加之文本判重算法，如BF、KMP、最长公共子串、后缀数组、字典树、DFA等计算时空复杂度并不适合数据量较大的工业应用场景。查找了相关资料，发现LSH(local sensitive )，即局部敏感哈希算法，可以应用本场景。
       LSH是指面对海量高维数据时，一般的算法无法快速降维查询相似度高的数据子集，利用特定的hash算法，将高维数据映射到低维空间，以较高概率快速寻找相似度高的数据子集。   满足以下两个条件的hash函数称为(d1,d2,p1,p2)-sensitive：

1、如果d(x,y) ≤ d1， 则h(x) = h(y)的概率至少为p1；

2、如果d(x,y) ≥ d2， 则h(x) = h(y)的概率至多为p2；
d(x,y)是x和y之间的一个距离度量，需要说明的是，并不是所有的距离度量都能够找到满足local sensitive的hash函数。

       由于这方面积累极少，自己写出的文章比较肤浅，所以直接整理粘贴大牛文章，在此表示感谢。

一、MinHash举例

下面原文转自大牛博客：聚类之MinHash　　　　　　　　

   　 MinHash是基于Jaccard相似度的算法，一种降维的方法X，Y两个集合：X= s1, s3, s6, s8, s9 ,Y= s3, s4, s7, s8, s10
MinHash的基本原理：在X∪Y这个大的随机域里，选中的元素落在A∩B这个区域的概率，这个概率就等于Jaccard的相似度
最小哈希：

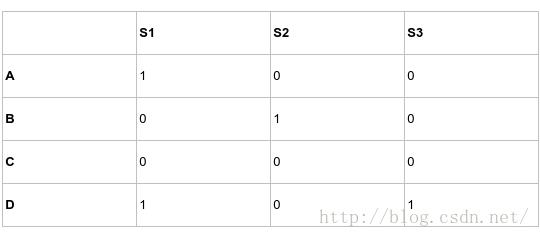
　行的随机排列转换，也称置换运算：


　　哈希值：排列转换后的行排列次序下第一个列值为1的行的行号，例如h(S1)=D，h(S2)=B。两个集合经随机排列之后得到的两个最小哈希值相等的概率等于这两个集合的Jaccard相似度。

二、MinHash原理

下面文章转资新浪大牛博客：基于MinHash的集合相似度计算原理 ，在此表示感谢！

　　首先，MinHash 是用于快速检测两个集合的相似性的方法。该方法由 Andrei Broder (1997) 发明，并最初用于AltaVista搜索引擎中来检测重复的网页。它同样可以用于大规模文档聚类中。
　 　 MinHash基于Jaccard相似性度量。对于两个集合X与Y，Jaccard相似性系数可以定义为：

　　 容易知道，该系数是0-1之间的值。当两个集合越接近，那么该值越接近1；反之，更接近0。
　　 假设h是一个哈希函数，将A与B的元素个数映射为一个整数。定义： hmin(S) 是集合S集合中具有最小哈希值的元素。那么，一个重要的结论是：仅当 X∪Y中具有最小哈希值的元素位于A∩B中时，hmin(X) = hmin(Y) 。而将哈希函数看成一个随机变量，那么任何X∪Y中的元素都有可能具有最小哈希值。因此，就有：
　　P[hmin(X) = hmin(Y)] = Jaccard(X,Y)
　　若令r 为一个随机变量（或者随机变量h的函数），当hmin(X) = hmin(Y) 时取1，否则取0。那么r 就是Jaccard(X,Y)的一个无偏估计。于是，自然而然地，计算两个集合的相似度Jaccard(X,Y)，我们便可以取n个哈希函数（n = 80或400等），计算对每个哈希函数，r 的取值，然后求平均即可。