∑GL-齐次坐标
Posted itzyjr
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了∑GL-齐次坐标相关的知识,希望对你有一定的参考价值。
目录
问题:两条平行线可以相交。
在欧几里德空间(几何学)中,同一平面上的两条平行线不能相交,也不能永远相交。这是每个人都熟悉的常识。
然而,这在投影空间中不再是真的,例如,下图中的火车轨道在远离眼睛时变得更窄。最后,两条平行轨道在地平线处相交,这是无限远处的一个点。

欧几里德空间(或笛卡尔空间)很好地描述了我们的2D/3D几何,但它们不足以处理射影空间(实际上,欧几里德几何是射影几何的一个子集)。二维点的笛卡尔坐标可以表示为(x,y)。
如果这一点远至无穷大呢?无穷远处的点是(∞,∞), 在欧几里得空间中变得毫无意义。在射影空间中,平行线应在无穷远处相交,但在欧几里德空间中不能相交。数学家们发现了一种解决这个问题的方法。
解决方案:齐次坐标
齐次坐标由August Ferdinand Möbius引入,使得在射影空间中计算图形和几何成为可能。齐次坐标是用N+1数字表示N维坐标的一种方法。
为了生成二维齐次坐标,我们只需在现有坐标中添加一个附加变量w。因此,笛卡尔坐标系中的点(X,Y)变成齐次坐标系中的点(x,y,w)。笛卡尔坐标系中的X和Y用齐次坐标系中的x、y和w重新表示:
X = x/w
Y = y/w
例如,笛卡尔(1,2)中的一个点变成了(1,2,1)中的齐次点。如果一个点(1,2)向无穷远移动,它在笛卡尔坐标系下就变成(∞,∞) ;它在齐次坐标系下变成(1,2,0),因为(1/0,2/0)≈ (∞,∞)。请注意,我们可以在无穷远处表示点,而不必使用“∞”。
为什么称为“齐次坐标”?
如前所述,为了将齐次坐标(x,y,w)转换为笛卡尔坐标,我们只需将x和y除以w;

将齐次坐标(Homogeneous)变换为笛卡尔坐标(Cartesian),我们可以发现一个重要的事实。让我们看看下面的例子:

如你所见,点(1,2,3)、(2,4,6)和(4,8,12)对应于相同的欧几里德点(1/3,2/3)。任何标量积(1a,2a,3a)与欧氏空间中的(1/3,2/3)是同一点。因此,这些点是“齐次的”,因为它们代表欧几里德空间(或笛卡尔空间)中的同一点。换句话说,齐次坐标是尺度不变的。
证据:两条平行线可以相交。
考虑欧氏空间中的下列线性系统:
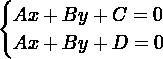
我们知道,上述两方程对应的是两条相互平行的线。
因为C≠D,所以上述方程没有解。
如果C=D,则两条线相同(重叠)。
让我们重写射影空间的方程,将x和y分别替换为x/w和y/w:
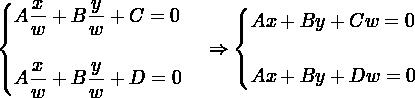
这时我们有解(x,y,0)。由于(C-D)w = 0,C≠D,所以w=0。因此,当(X,Y,W)=(x,y,0)时满足两个方程,即两条平行线相交于点(x,y,0),对应欧氏空间中点(x/0,y/0),这是一个在无穷远处的点。
齐次坐标是计算机图形学中非常有用的基本概念,例如将三维场景投影到二维平面上。
以上是关于∑GL-齐次坐标的主要内容,如果未能解决你的问题,请参考以下文章