785. 判断二分图

Posted 2022-04-13 hequnwang10

一、题目描述

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：
不存在自环（graph[u] 不包含 u）。
不存在平行边（graph[u] 不包含重复值）。
如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。
二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

示例 1：

输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

示例 2：

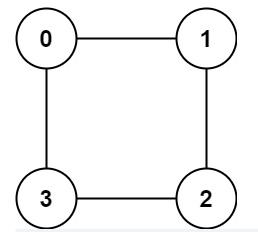
输入：graph = [[1,3],[0,2],[1,3],[0,2]]
输出：true
解释：可以将节点分成两组: 0, 2 和 1, 3 。

二、解题

DFS

使用深度优先遍历对节点染色，相邻的两个点染成不同的颜色，若发现当前节点和需要染色的颜色不相等返回false。

class Solution 
    public boolean isBipartite(int[][] graph) 
        //标记染色数组
        int[] colors = new int[graph.length];
        //每个点的初始颜色是0，判断当前节点是否被染色，没有被染色 就将其染色成1，然后该节点的相邻节点染相反颜色。
        for(int i = 0;i<graph.length;i++)
            if(colors[i] == 0 && !dfs(graph,colors,i,1))
                return false;
            
        
        return true;
    
    public boolean dfs(int[][] graph,int[] colors,int v,int color)
        //当前节点如果不是0，则判断当前节点的颜色是否与需要染色的颜色相等
        if(colors[v] != 0)
            return colors[v] == color;
        
        //将当前节点染色
        colors[v] = color;
        //将当前节点的相邻节点染色相反颜色
        for(int node:graph[v])
            if(!dfs(graph,colors,node,-color))
                return false;
            
        
        return true;
    

BFS

图搜索算法从各个连通域的任一顶点开始遍历整个连通域，遍历的过程中用两种不同的颜色对顶点进行染色，相邻顶点染成相反的颜色。这个过程中倘若发现相邻的顶点被染成了相同的颜色，说明它不是二分图；反之，如果所有的连通域都染色成功，说明它是二分图。

class Solution 
    public boolean isBipartite(int[][] graph) 
        //标记染色数组
        int[] visited = new int[graph.length];
        //广度优先遍历
        Queue<Integer> queue = new LinkedList<>();
        for(int i = 0;i<graph.length;i++)
            //首先判断当前顶点是否未被访问
            if(visited[i] != 0)
                continue;
            
            //每出队一个顶点，将其所有相邻节点染色成相反颜色并入队
            queue.add(i);
            visited[i] = 1;
            while(!queue.isEmpty())
                int v = queue.poll();
                for(int w : graph[v])
                    //如果当前顶点的相邻节点被染色了，且颜色与当前节点颜色相同，则返回false；
                    if(visited[w] == visited[v])
                        return false;
                    
                    if(visited[w] == 0)
                        visited[w] = -visited[v];
                        queue.add(w);
                    
                
            
        
        return true;