重要概念与题型总结
Posted Leokadia Rothschild
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了重要概念与题型总结相关的知识,希望对你有一定的参考价值。
编译原理1-3章重要概念与题型总结
文章目录
1-2章概念测试题总结:




程序语言的语法描述



V ∗ V^* V∗和 V + V^+ V+区别在于,如果V中间原来没有空字,闭包中包含空字,正规闭包没有空字




句型、句子和语言

题型一:证明某表达式是文法的句子:
- 首先要证明是该表达式是文法的一个句型:能够从文法的开始符号推出来。也就是给出来一个从文法的开始符号到你要推导的序列。
- 再证明该句型仅含终结符

要证明是一个句子
- 必须证明它只有终结符
- 再证明它能从文法的开始符号推出来
题型二:求文法产生的语言:
解题思路:先分析下文法可能产生的推导,然后总结出语言的模式。

使用第一个候选推导停止,使用第二个候选,在右边增加b
每次使用递归候选替换时,都会导致句型变长,这样就能推出结构相似长度不同的句子。

S推出AB
S所能推导的式子都可以看成两个部分,前一部分由A推导出来,后一部分由语法单位B产生。
继续分析A,B产生串的特点
A的候选,aA递归候选(不断在A前面增加a),a非递归候选(使用即结束)
A最终产生的串就是若干个a构成的串(个数>0)
B的候选,bB递归候选(不断在B面增加a),b非递归候选(使用即结束)
B最终产生的串就是若干个b构成的串(个数>0)
题型三:由产生串反推文法:
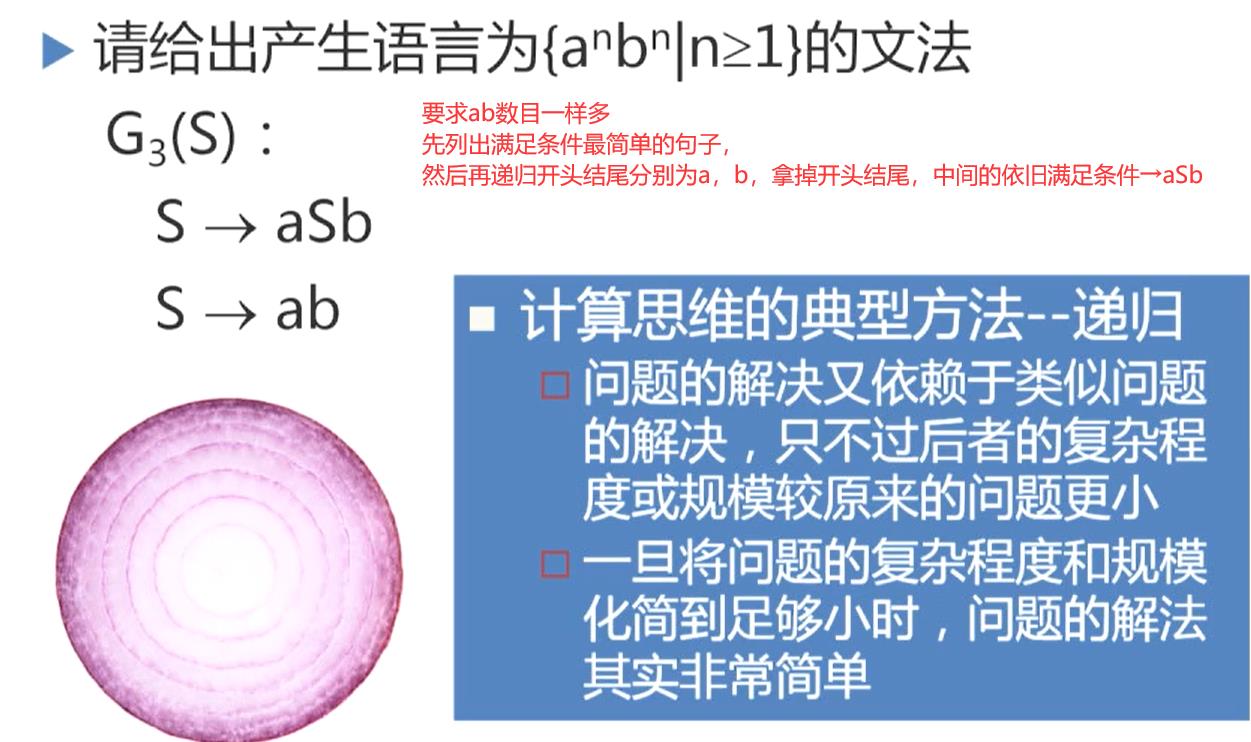
关键性约束:a,b数目一样多
- 拿掉开头的子串,剩下的子串也满足条件:前一半若干个a,后一半若干个b,数目相同,所以可以写出规则S→aSb
- 最后不断拿掉,最简单的句子是ab,S→ab递归基础

句子特点:前面若干个a后面若干个b,a的数目是b的1到2倍之间。
- 首先找出满足条件最简单的句子:S→ab|aab
- 递推:S→aSb|aaSb
题型四:写出最左推导/最右推导,并画出语法树
最左推导和最右推导

最左推导和最右推导的语法树是一样的,只是树的生长顺序不同,从上往下(从左到右|从右到左生长)
语法树
用一张图表示一个句型的推导,称为语法树

如果使用最左(右)推导,则一个最左(右)推导与语法树一一对应。
文法层面的二义性

- 文法的二义性:如果一个文法存在某个句子对应两颗不同的语法树,则说这个文法是二义的。
G(E): E → i|E+E|E*E|(E) 是二义文法。
题型五:证明某文法是二义文法:

只要找出他的一个有两颗不同的语法树这样的句型/句子就能证明这个文法是二义的。
同理,只要找到一个有两个不同的最左推导/最右推导的句子/句型也能证明这个文法是二义的。
语言层面的二义性
- 语言的二义性:一个语言是二义性的,如果对它不存在无二义性的文法。
- 对于语言L,可能存在G和G’,使得L(G)=L(G’)=L,但可能其中一个为二义的,一个为无二义的。
- 二义性问题是不可判定问题,即不存在一个算法,它能在有限步骤内,确切地判定一个文法是否是二义的。
- 可以找到一组无二义文法的充分条件。


判断文法是否是二义的:


形式语言鸟瞰
- Chomsky于1956年建立形式语言体系,他把文法分成四种类型:0,1,2,3型。
- 与上下文无关文法一样,它们都由四部分组成,但对产生式的限制有所不同。

题型六:掌握0,1,2,3型文法,要求能根据语言按要求写出相对应符合条件的0,1,2,3型文法
0型(短语文法,图灵机):
产生式形如:
α
→
β
α→β
α→β
其中:
α
∈
(
V
T
∪
V
N
)
∗
α∈ (V_T∪V_N)^*
α∈(VT∪VN)∗且至少含有一个非终结符;
β
∈
(
V
T
∪
V
S
)
∗
β∈ (V_T∪V_S)^*
β∈(VT∪VS)∗
α、β都是由终结符和非终结符组成的任意串,但α含有一个非终结符(全是终结符就没法定义了)
2型文法(上下文无关文法是0型文法的一个特例)
1型(上下文有关文法,线性界限自动机):
产生式形如:
α
→
β
α→β
α→β
其中:
α
∈
(
V
T
∪
V
N
)
∗
α∈ (V_T∪V_N)^*
α∈(VT∪VN)∗且至少含有一个非终结符;
β
∈
(
V
T
∪
V
S
)
∗
β∈ (V_T∪V_S)^*
β∈(VT∪VS)∗
∣
α
∣
≤
∣
β
∣
|α| ≤ |β|
∣α∣≤∣β∣,仅
S
→
ε
S→ε
S→ε 例外。
左边一定比右边短
2型(上下文无关文法,非确定下推自动机):
产生式形如:
A
→
β
A → β
A→β
其中:
A
∈
V
N
;
β
∈
(
V
T
∪
V
N
)
∗
A∈ V_N;β∈ (V_T ∪ V_N)^*
A∈VN;β∈(VT∪VN)∗
左边是一个非终结符,右边是终结符非终结符组成的任意串。
3型(正规文法,有限自动机):
右线性文法
产生式形如:
A
→
α
B
或
A
→
α
A → αB 或 A → α
A→αB或A→α
其中:
α
∈
V
T
∗
;
A
,
B
∈
V
N
α∈ V_T^*;A,B∈V_N
α∈VT∗;A,B∈VN
右边要么没有非终结符
如果有非终结符的话,只能出现在最右边。
左线性文法
产生式形如:
A
→
B
α
或
A
→
α
A → Bα 或 A → α
A→Bα或A→α
其中:
α
∈
V
T
∗
;
A
,
B
∈
V
N
α∈ V_T^*;A,B∈V_N
α∈VT∗;A,B∈VN
右边要么没有非终结符
非终结符要出现,只能在定义式的最左边。




是个2型文法不是3型文法,S出现在候选式中间,不是最左边也不是最右边,只能由上下文无关文法来产生,不能由正规文法来产生
计算机科学理论可以证明,像 a n b n a^nb^n anbn这种自嵌套的语言只能由上下文无关文法来描述,不能由正规文法来描述
举例:


第三章

小概念:单词的长度不能超过半区的长度,半区的长度就是程序语言允许的最大长度
如果标识符长度不能超过128,就可以推断出扫描缓冲区的长度为256
正规式和正规集

程序语言定义合法单词的集合就是正规集
为了更好的表示正规集,我们用正规式作为正规集的代表/命名。
对给定的字母表
∑
∑
∑
1)
ε
ε
ε和
Ф
Ф
Ф都是
∑
∑
∑上的正规式,它们所表示的正规集为
ε
ε
ε和
Ф
Ф
Ф;
2) 任何
a
∈
∑
a∈ ∑
a∈∑,a是
∑
∑
∑上的正规式,它所表示的正规集为a ;
3) 假定e1和e2都是
∑
∑
∑上的正规式,它们所表示的正规集为L(e1)和L(e2),则
- i) (e1|e2)为正规式,它所表示的正规集为L(e1)∪L(e2),(两个正规集的并还是正规集)
- ii) (e1.e2)为正规式,它所表示的正规集为L(e1)L(e2),(两个正规集的连接还是正规集)
- iii) ( e 1 ) ∗ (e1)^* (e1)∗为正规式,它所表示的正规集为 ( L ( e 1 ) ) ∗ (L(e1))^* (L(e1))∗,(一个正规集的闭包还是正规集)
仅由有限次使用上述三步骤而定义的表达式才是 ∑ ∑ ∑上的正规式,仅由这些正规式表示的字集才是 ∑ ∑ ∑上的正规集
Ф
Ф
Ф/ 既是集合也是正规式也是正规集
不是字符也不是由字母表字符构成的字符串,因此其不是字
ε ε ε既是字也是正规式,其正规集是 ε ε ε
a是字母表中的字符
则a是字符,当然a也可以看成一个由一个字符a构成的长度为1的字符串,因此a是字
根据定义a也是正规式
其对应的正规集为a


VS
ε
ε
ε
这两个集合都是正规集,空集对应的正规式是
Ф
Ф
Ф这个符号,而
ε
ε
ε所对应的正规式是
ε
ε
ε,
ε
ε
ε集合中有一个元素(字)尽管字的长度是0,而空集里面没有任何元素。

回顾:



题型——证明正规式等价
对给定的字母表
∑
∑
∑ 以上是关于重要概念与题型总结的主要内容,如果未能解决你的问题,请参考以下文章
1)
ε
ε
ε和
Ф
Ф
Ф都是
∑
∑
∑上的正规式,它们所表示的正规集为