德尔塔公式是啥？

Posted 2023-03-27

“德尔塔”表示关于x的一元二次方程ax²+bx+c=0的根的判别式，其符号为“△”

其只取决于一元二次方程各项的系数：△=b²-4ac

△的值决定一元二次方程根的情况：

（1）△＞0时；方程有两个不相等的实数根

（2）△=0时；方程有两个相等的实数根 此时，ax²+bx+c是一个完全平方式

（3）△＜0时；方程没有实数根

扩展资料

一元二次方程有4种解法，即直接开平方法、配方法、公式法、因式分解法。

1、公式法可以解所有的一元二次方程，公式法不能解没有实数根的方程（也就是b^2-4ac<0的方程）。

2、因式分解法，必须要把等号右边化为0。

3、配方法比较简单：首先将方程二次项系数a化为1，然后把常数项移到等号的右边，最后后在等号两边同时加上一次项系数绝对值一半的平方。

4、求根公式： x=-b±√(b^2-4ac)/2a。

一般地，式子b^2－4ac叫做一元二次方程ax^2＋bx＋c＝0根的判别式，通常用希腊字母“Δ”表示它，即Δ＝b^2－4ac。

1、当Δ>0时，方程ax^2＋bx＋c＝0(a≠0)有两个不等的实数根；

2、当Δ＝0时，方程ax^2＋bx＋c＝0(a≠0)有两个相等的实数根；

3、当Δ<0时，方程ax^2＋bx＋c＝0(a≠0)无实数根。

参考技术A

“德尔塔”表示关于x的一元二次方程ax²+bx+c=0的根的判别式，其符号为“△”

其只取决于一元二次方程各项的系数：△=b²-4ac

△的值决定一元二次方程根的情况：

当（1）△＞0时 方程有两个不相等的实数根

（2）△=0时 方程有两个相等的实数根 此时，ax²+bx+c是一个完全平方式

（3）△＜0时 方程没有实数根

扩展资料：

因式分解法即利用因式分解求出方程的解的方法。

因式分解法解一元二次方程的一般步骤如下：

①移项，使方程的右边化为零；

②将方程的左边转化为两个一元一次多项式的乘积；

③令每个因式分别为零

参考资料来源：百度百科-一元二次方程

参考技术B

“德尔塔”表示关于x的一元二次方程ax²+bx+c=0的根的判别式，其符号为“△”

其只取决于一元二次方程各项的系数：△=b²-4ac

△的值决定一元二次方程根的情况：

（1）△＞0时 方程有两个不相等的实数根

（2）△=0时 方程有两个相等的实数根 此时，ax²+bx+c是一个完全平方式

（3）△＜0时 方程没有实数根

扩展资料

一元二次方程成立必须同时满足三个条件：

①是整式方程，即等号两边都是整式，方程中如果有分母；且未知数在分母上，那么这个方程就是分式方程，不是一元二次方程，方程中如果有根号，且未知数在根号内，那么这个方程也不是一元二次方程（是无理方程）。

②只含有一个未知数；

③未知数项的最高次数是2。

参考技术C 德尔塔”表示关于x的一元二次方程ax²+bx+c=0的根的判别式，其符号为“△”
其只取决于一元二次方程各项的系数：△=b²-4ac
△的值决定一元二次方程根的情况：
（1）△＞0时；方程有两个不相等的实数根
（2）△=0时；方程有两个相等的实数根 此时，ax²+bx+c是一个完全平方式
（3）△＜0时；方程没有实数根 参考技术D 德尔塔那些公式。 方程ax²+bx+c=0 (a≠0)的根的判别式Δ=b²-4ac.若Δ>0,则方程有两个相异的实根；若Δ=0，则方程有两个相同的实根；若Δ<0，则方程无实根.德尔塔公式例子。

[计算机数值分析]高斯-塞德尔迭代公式解线性方程组

在雅可比迭代公式的基础上，对于收敛的迭代过程，所求出的“新值”常比“老值”更准确些，因此可以用它替代老值作进一步的计算，这样的思想就是著名的高斯-塞德尔迭代公式。
如下图叙述：

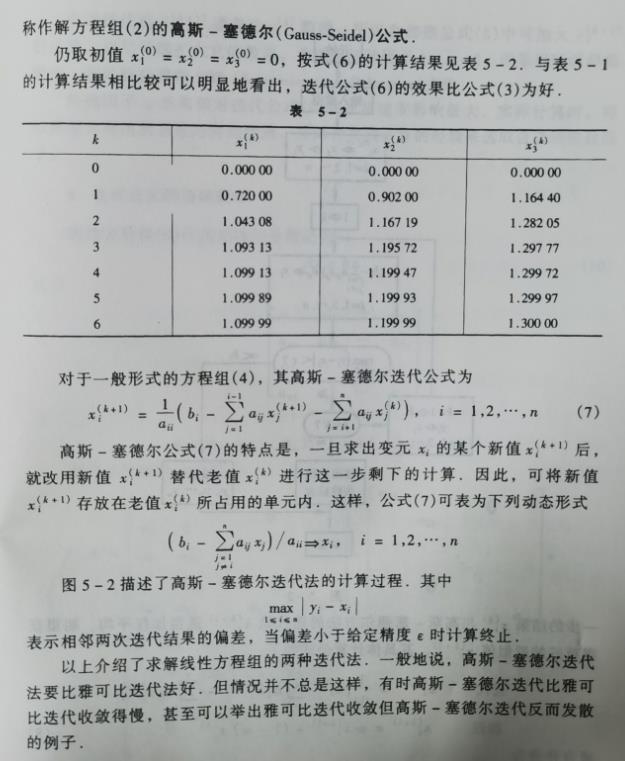
• 运行示例：

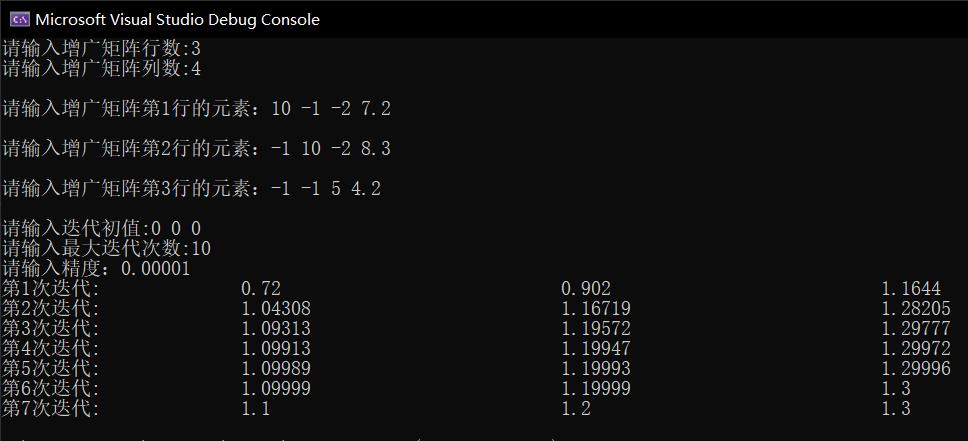
• 源码：

#include<iostream>
#include<iomanip>
#define MAX 10
using namespace std;

int main(void)

	double a[MAX][MAX];   //二维数组存储原始方程组的增广矩阵

	int row, col;

	cout << "请输入增广矩阵行数:";   //行数，即方程个数
	cin >> row;

	cout << "请输入增广矩阵列数:";   //列数，包含常数项
	cin >> col;

	cout << endl;

	//增广矩阵输入提示，按行输入
	for (int i = 1; i <= row; i++)
	
		cout << "请输入增广矩阵第" << i << "行的元素：";

		for (int j = 1; j <= col; j++)
		
			cin >> a[i][j];
		
		cout << endl;
	

	//对元素进行处理
	for (int i = 1; i <= row; i++)
	
		for (int j = 1; j <= col; j++)
		
			if (i != j && j != col)
			
				a[i][j] /= -a[i][i];   //非行列坐标相等的元素除以负行列坐标相等的元素
			
			if (j == col)
			
				a[i][j] /= a[i][i];   //常数项除以行列相等的元素
			
		
	

	//对a[1][1]、a[2][2]......赋值为0
	for (int i = 1; i <= row; i++)
	
		a[i][i] = 0;
	

	double b[MAX]; //记录每次迭代后的值
	
	//迭代初值
	cout << "请输入迭代初值:";
	for (int i = 1; i < col; i++)   //用数组b记录每次迭代后的x的值，用于下次迭代
	
		cin >> b[i];
	

	int N;   //允许的最大迭代次数

	cout << "请输入最大迭代次数:";
	cin >> N;

	double accuracy;   //精度
	double error = 0;   //相邻两次迭代结果的误差

	cout << "请输入精度：";
	cin >> accuracy;

	for (int i = 1; i <= N; i++)   //最多允许迭代N次
	
		cout << "第" << i << "次迭代:";

		int count = 1;   //用count控制迭代值按每行col-1个输出，即自变量个数输出

		for (int j = 1; j <= row; j++)   //每一次迭代(i)，求取每一行的行列坐标相等的值即a[j][j]
		
			double item;   //中间变量

			for (int k = 1; k <= col; k++)   //j循环一次，j循环col次，求得a[j][j]
			
				if (j == k)   //如果j=k，继续
				
					continue;
				

				if (k != col)   //如果j不等于k且不等于常数项的下标
				
					item = a[j][k] * b[k];   //则每一项等于系数与对应迭代初值的乘积
				
				else
				
					item = a[j][col];   //j=col即常数项下标时，直接加上常数项，不对常数项处理
				

				a[j][j] += item;   //累加item，求的a[1][1],a[2][2]......
			
			cout << "\\t\\t" << a[j][j] << "\\t\\t";  //输出a[1][1],a[2][2]......

			error = abs(a[count][count] - b[count]);  //相邻两次迭代结果的偏差

			b[count] = a[count][count];  //更新b[]里的值为本次迭代结束的值

			a[count][count] = 0;   //赋a[1][1],a[2][2]......值为0，避免拥有初值影响下一次迭代结果

			if (count % (col - 1) == 0)   //控制元素输出个数
				cout << endl;
			count++;
		
		
		if (error <= accuracy)   //解符合精度要求,直接结束迭代过程
		
			break;
		

		if (error > accuracy && i <= N)     //解不符合精度要求但未超过最大迭代次数，继续迭代
		 
			continue;
		
		else   //超过最大迭代次数，输出提示
		
			cout << "达到允许的最大迭代次数，未找到符合精度要求的根！" << endl;