[概率论与数理统计-5]:一元连续随机变量=>几何图形=>样本空间=>组合样本=>长度/面积/体积=>几何概率
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[概率论与数理统计-5]:一元连续随机变量=>几何图形=>样本空间=>组合样本=>长度/面积/体积=>几何概率相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123727473
目录
第1章 什么是几何概率
几何概率是可以用几何方法求得的现实生活中复合事件的概率。
比如,向某一可度量的区域内投一质点,如果所投的点落在门中任意区域 g 内的可能性大小与 g 的度量成正比,而与 g 的位置和形状无关,则称这个随机试验为几何型随机试验或几何概型,此处的度量就是测度,一维指长度,二维指面积,三维指体积等。
几何概型是一种求解现实问题的概率模型。
在这个模型下,随机实验所有可能的结果是无限的,并且每个基本结果发生的概率是相同的。例如一个人到单位的时间可能是8:00~9:00之间的任意一个时刻;往一个方格中投一个石子,石子落在方格中任何一点上……这些试验出现的结果都是无限多个(所以只能可以通过求长度、面积、体积来完成概率的计算),属于几何概型。
一个试验是否为几何概型在于,这个试验的基本事件是否具有几何概型的两个特征:无限性和等可能性(等概率分布),只有同时具备这两个特点的概型才能用几何概型(长度、面积、体积)求解现实的概率问题。
第2章 几何概率的关键点:
2.1 如何用连续的几何图形的区域表示离散的生活事件:
- 基础:可以把x,y坐标看成是连续事件,几何图形(线段或面积或体积)看成是组合事件(是有无数个连续的点组成)
- 生活事件转换为几何图形(组合事件),再转换为基本事件,经过这个转换,生活的离散事件就转换成了离散的几何图形组合事件,而每个几何图形的组合事件,又是连续的空间点组成。
- 样本空间:所有基本事件(样本)构成的总的几何图形(线段或面积或体积)
- 组合事件:符合事件构成的几何图形(线段或面积或体积)
2.2 如何求组合事件的概率:
假设条件:所有基本事件(样本)落在样本空间的位置是等概率的。
计算概率:有了(1)的转换,组合事件的概率=组合事件的图形(线段或面积或体积)除以样本空间的图形(线段或面积或体积)

2.3 几何概率的计算

A: 复合事件
S: 样本空间
P: 概率
几何度量(长度、面积、体积)
2.4 几何概率与n元随机变量
在几何概率中,基本事件是空间中的一个质点,
每个质点是n维度的随机变量组成:
几何线段:一元随机变量(X)
面积:二元随机变量(X,Y)
空间体积:三元随机变量(X,Y,Z)
输出:联合概率分布,即复合事件覆盖的(长度或面积或体积)除以样本空间空间总的(长度或面积或体积)。
第3章 几何概率的案例
3.1 一维:几何度量体现为长度。
【例1】出租车司机李师傅有午睡习惯。一天,他睡午觉醒来,发现手机没电了,手表也停了,于是他只能打开收音机等待交通电台整点报时,如果他等待报时时间不超过15分钟,则这种可能性大小为( )
A、1/2 B、1/3 C、1/4 D、1/6
【解析】C。
如图所示,设想一条时间轴两个刻度时间相差1小时,李师傅醒来的时刻落在距离在刻度点15分钟范围可保证等待不超过15分钟,因此概率为15/60=1/4,选C。
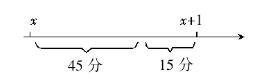
随机变量:等待的时间长度,用X表示,单位为分钟。
随机事件:事件变量的取值范围就是随机事件,这里是【0,60】分钟之间的任意值。
样本空间:整点报时,每一个小时报一次,样本空间为1小时,即60分钟。
复合事件:不超过15分钟属于复合事件,由无数个基本事件点组成,长度小于15分钟,最大为15分钟时长
概率计算:李师傅醒来的基本事件点,如果落在x+1附件的复合事件中时,这时候的等待事件长度不超过15分钟,这个15分钟的复合事件的取值占整个样本空间基本事件的取值的15/60=1/4.
3.2 二维:几何度量体现为面积。
【例2】小波通过往圆圈里投掷米粒(米粒本身长度不计,视为一个点)的方式决定自己的周末活动。经过试验,他将米粒投进圆圈内的成功率达到100%,但投掷在圆内的位置随机。如果米粒到圆心的距离大于圆半径的一半,那么他周末去看电影;若米粒到圆心的距离小于半径的 ,他会去打篮球;否则,他将在家看书。据此可知小波周末不在家看书的概率为:
A、13/16 B、2/5 C、3/5 D、1/16
【解析】A。投掷米粒在圆圈内任一点是等可能的,且结果有无限种可能,属于几何概率。如图所示,假设大圆圈的半径为4、面积=π×42=16π;打篮球的面积=π、看电影的面积=16π-4π=12π,所以不看书的概率=(π+12π)/(16π)=13/16,选A。

随机变量:在圆平面中的落点,二维随机变量(x,y)组成,且x^2 + y^2< r^2.
随机事件:随机变量的取值范围就是随机事件(X,Y)
样本空间:由于是圆,整个圆筒的底面积就是整个样本空间。
复合事件:复合事件与现实问题相关,这里的三个复合事件包括
- 最小圆的的面积的区域
- 中间圆面积-最小圆面积的区域
- 最外层圆面积-中间圆面积的区域
概率计算:李师傅醒来的基本事件点,如果落在x+1附件的复合事件中时,这时候的等待事件长度不超过15分钟,这个15分钟的复合事件的取值占整个样本空间基本事件的取值的15/60=1/4.
【例3】甲乙两人相约见面,并约定第一人到达后,等15分钟不见第二人来就可以离去。假设他们都在10点至10点半的任一时间来到见面地点,则两人能见面的概率有多大?
A. 37.5% B. 50% C. 62.5% D. 75%
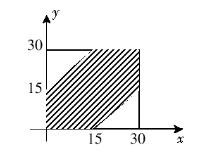
【中公解析】D。如图所示,x、y分别代表甲乙两人到达的时间,两人能够见面的条件是,即图中阴影部分,则所求概率为阴影部分面积占大正方形的面积的比例,即为甲乙能见面的概率,阴影部分面积=30×30-2×1/2×15×15=675,所求概率为675/900=75%,选D。
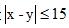
3.3 三维:几何度量体现为体积。
【例4】半径为4的球体,有一点落于球体内,此点到球心距离都小于2的概率是多少?
【中公解析】该点在球内有无限种可能,而每种可能性相同,属于几何概率。如图所示,在球内随机取一点,使这个点到球心的距离小于2,说明点落在与大球球心相同,半径为2的小球的内部,体积为,整个打的球体体积为,则所求概率。
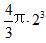
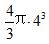
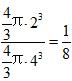

作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123727473
以上是关于[概率论与数理统计-5]:一元连续随机变量=>几何图形=>样本空间=>组合样本=>长度/面积/体积=>几何概率的主要内容,如果未能解决你的问题,请参考以下文章