怎样才能深刻理解递归和回溯？

Posted 2023-03-25

现在能看懂递归和回溯的程序，但写不出来，看解题报告一看是这么一回事，但自己写就不行了，感觉自己对递归和回溯没有真正理解他的原理和内涵，想不通。。纠结。。。求助各位大虾们，帮帮忙，助我一臂之力啊。

递归是一种算法结构，回溯是一种算法思想，一个递归就是在函数中调用函数本身来解决问题，回溯就是通过不同的尝试来生成问题的解，有点类似于穷举，但是和穷举不同的是回溯会“剪枝”，意思就是对已经知道错误的结果没必要再枚举接下来的答案了，比如一个有序数列1,2,3,4,5，要找和为5的所有集合，从前往后搜索我选了1，然后2，然后选3 的时候发现和已经大于预期，那么4,5肯定也不行，这就是一种对搜索过程的优化。
回溯分析是追踪决策的特性之一。 是指对原始决策的产生机制、决策内容、主客观环境等进行分析．从起点开始，按顺序考察导致决策失误的原因、问题的性质、失误的程度等。
[算法分析]
为了描述问题的某一状态，必须用到它的上一状态，而描述上一状态，又必须用到它的上一状态……这种用自已来定义自己的方法，称为递归定义。例如：定义函数f(n)为：
f(n)=n*f(n－1) (n>0)
f(n)=1 (n=0)
则当0时，须用f(n-1)来定义f(n),用f(n-1-1)来定义f(n-1)……当n=0时，f(n)=1。
由上例我们可看出，递归定义有两个要素：
（1）递归边界条件。也就是所描述问题的最简单情况，它本身不再使用递归的定义。
如上例，当n=0时，f(n)=1，不使用f(n-1)来定义。
（2）递归定义：使问题向边界条件转化的规则。递归定义必须能使问题越来越简单。
如上例：f(n)由f(n-1)定义，越来越靠近f(0),也即边界条件。最简单的情况是f(0)=1。
递归算法的效率往往很低, 费时和费内存空间. 但是递归也有其长处, 它能使一个蕴含递归关系且结构复杂的程序简介精炼, 增加可读性. 特别是在难于找到从边界到解的全过程的情况下, 如果把问题推进一步,其结果仍维持原问题的关系, 则采用递归算法编程比较合适.
递归按其调用方式分为: 1. 直接递归, 递归过程P直接自己调用自己; 2. 间接递归, 即P包含另一过程D, 而D又调用P.
递归算法适用的一般场合为:
1. 数据的定义形式按递归定义.
如裴波那契数列的定义: f(n)=f(n-1)+f(n-2); f(0)=1; f(1)=2.
对应的递归程序为:
Function fib(n : integer) : integer;
Begin
if n = 0 then fib := 1 递归边界
else if n = 1 then fib := 2
else fib := fib(n-2) + fib(n-1) 递归
End;
这类递归问题可转化为递推算法, 递归边界作为递推的边界条件.
2. 数据之间的关系(即数据结构)按递归定义. 如树的遍历, 图的搜索等.
3. 问题解法按递归算法实现. 例如回溯法等.
从问题的某一种可能出发, 搜索从这种情况出发所能达到的所有可能, 当这一条路走到" 尽头 "
的时候, 再倒回出发点, 从另一个可能出发, 继续搜索. 这种不断" 回溯 "寻找解的方法, 称作
" 回溯法 ".

[参考程序]
下面给出用回溯法求所有路径的算法框架. 注释已经写得非常清楚, 请读者仔细理解.
Const maxdepth = ????;
Type statetype = ??????; 状态类型定义
operatertype = ??????; 算符类型定义
node = Record 结点类型
state : statetype; 状态域
operater :operatertype 算符域
End;
注: 结点的数据类型可以根据试题需要简化
Var
stack : Array [1..maxdepth] of node; 存当前路径
total : integer; 路径数
Procedure make(l : integer);
Var i : integer;
Begin
if stack[L-1]是目标结点 then
Begin
total := total+1; 路径数+1
打印当前路径[1..L-1];
Exit
End;
for i := 1 to 解答树次数 do
Begin
生成 stack[l].operater;
stack[l].operater 作用于 stack[l-1].state, 产生新状态 stack[l].state;
if stack[l].state 满足约束条件 then make(k+1);
若不满足约束条件, 则通过for循环换一个算符扩展
递归返回该处时, 系统自动恢复调用前的栈指针和算符, 再通过for循环换一个算符扩展
注: 若在扩展stack[l].state时曾使用过全局变量, 则应插入若干语句, 恢复全局变量在
stack[l-1].state时的值.
End;
再无算符可用, 回溯
End;
Begin
total := 0; 路径数初始化为0
初始化处理;
make(l);
打印路径数total
End. 参考技术A 递归的精华就在于大问题的分解，要学会宏观的去看问题，如果这个大问题可以分解为若干个性质相同的规模更小的问题，那么我们只要不断地去做分解，当这些小问题分解到我们能够轻易解决的时候，大问题也就能迎刃而解了。如果你能独立写完递归创建二叉树，前序、中序、后序递归遍历以及递归计算二叉树的最大深度，递归就基本能掌握了。

回溯本人用得很少，仅限于八皇后问题，所以帮不上啥了。本回答被提问者采纳

递归与回溯4：一文彻底理解回溯

1.回溯大白话

关于回溯，先用大白话说几个结论：

1.回溯能干什么？

主要解决那些暴力枚举也无法解决的问题。

2.回溯与递归是什么关系？

回溯是递归的纵横拓展，主要是递归（纵）+局部暴力枚举（横）。所以你可以从递归和暴力两个方面来拆解回溯问题。

3.回溯的关键在于“回”上，也就是要撤销，为什么要撤销？

因为回溯本质上仍然是枚举，你不喜欢她的前任，你要将她前任的所有东西都仍然，然后才愿意重新开始！就这么回事。

4.回溯经常看到“剪枝”，什么是剪枝，为什么要剪枝？

剪枝就是去掉那些不必要的递归，从而提高执行效率。假如有五个男孩子都和一个女生说要厮守终生。她会和这五个人都先过一辈子再确定谁会真正做到吗？当然不会。而是会先思考一下，有一个可能导出勾勾搭搭，那她可以认为这个人只是一时兴起，剪掉！有一个可能太窝囊了，什么都不会，那她可以认为和他在一起会非常累，剪掉！有一个长得太对不起祖宗，可能会影响下一代，剪掉！最后就剩下两个，再进一步考虑！这就是剪枝！

5.回溯问题很典型吗？

非常典型，主要是组合、分割、子集、排列，棋盘等以及拓展。

组合问题:N个数里面按一定规则找出k个数的集合

切割问题:一个字符串按一定规则有几种切割方式

子集问题:一个N个数的集合里有多少符合条件的子集

排列问题:N个数按一定规则全排列，有几种排列方式 棋

盘问题:N皇后，解数独等等。

6.回溯代码有模板吗？

有！基本模板是：

    void backtracking(参数) 
        if (终止条件) 
            存放结果;
            return;
        
        for (选择本层集合中元素（画成树，就是树节点孩子的大小）)
            处理节点;
            backtracking();
            回溯，撤销处理结果;
        
    

7.上面的模板中本层集合元素是怎么确定的？怎么画成树？

大部分回溯问题的集合与如下的结构类似，而确定集合元素就是枚举任一元素的所有可能，有几种可能，就对应第二层就有几个结点。

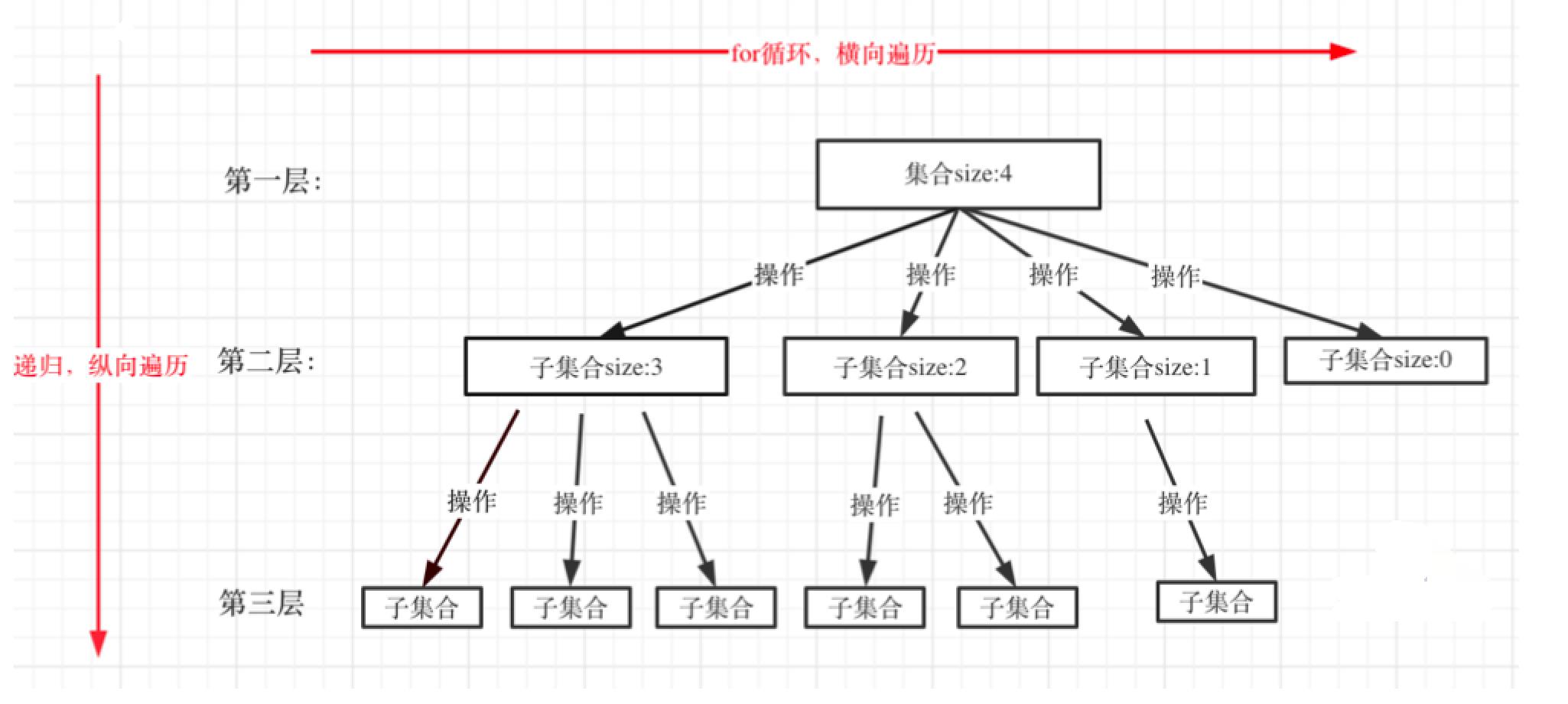
看完之后是不是感觉没有想象中那么难了？ 

2.从N叉树开始聊回溯

我们知道在二叉树中，按照前序遍历的过程如下所示：

public static void treeDFS(TreeNode root) 
    if (root == null)
        return;
    System.out.println(root.val);
    treeDFS(root.left);
    treeDFS(root.right);

假如我现在是一个三叉、四叉甚至N叉树该怎么办呢？很显然这时候就不能用left和right来表示分支了，使用一个List比较好，也就是大致这样来遍历;

public static void treeDFS(TreeNode root) 
    //递归必须要有终止条件
    if (root == null)
        return;
    System.out.println(root.val);

    //通过循环，分别遍历N个子树
    for (int i = 1; i <= N; i++) 
        //2，一些操作，可有可无，视情况而定

        treeDFS("第i个子节点");

        //3，一些操作，可有可无，视情况而定
    

到这里，你有没有发现和刚刚说的回溯的模板非常像了？是的！基本框架非常像。

这里的参数和某些代码的含义等暂且不提，只是先告诉自己，回溯的框架就是遍历N叉树。

3.为什么有的问题暴力搜索也不行了？

我们前面说回溯主要解决一些暴力枚举也无法解决的问题，什么问题这么神奇，暴力都无法解决呢？看个例子：

LeetCode77 ：给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。例如，输入n=4，k=2，则输出：

[
[2,4], [3,4], [2,3], [1,2], [1,3], [1,4]
]

如果让我们说过程，就是这样：n=4，那就是所有的数字为1,2,3,4

1. 先取一个1，则有[1,2]，[1,3]，[1,4]三种可能。
2. 然后取一个2，因为1已经取过了，所以不再取，则有[2,3]，[2,4]两种可能。
3. 再取一个3，因为1和2都取过了，所以不再取，则有[3,4]一种可能。
4. 再取4，因为1，2，3都已经取过了，所以直接返回null。

这就是我们思考该问题的基本过程，写成代码也很容易，双层循环轻松搞定：

 int n = 4;
        for (int i = 1; i <= n; i++) 
            for (int j = i + 1; j <= n; j++) 
                System.out.println(i + " " + j);
            
        

假如n和k都变大，比如n是200，k是3呢？也可以，三层循环基本搞定：

 int n = 200;
  for (int i = 1; i <= n; i++) 
       for (int j = i + 1; j <= n; j++) 
            for (int u = j + 1; u <= n; n++) 
               System.out.println(i + " " + j + " " + u);
             
        
   

如何这里的K是5呢？甚至是50呢？你需要套多少层循环？甚至告诉你K就是一个未知的正整数k，你怎么写循环呢？是不是发现这时候已经无能为例了？所以暴力搜索就不行了。

这种类型的问题就要考虑使用回溯了，这就是组合问题，除此之外子集、排列、切割、棋盘等方面都有类似的问题。

4 回溯=递归+局部暴力枚举

前面说回溯就是对递归进行纵横拓展，纵向就是递归，用来解决多层嵌套问题，因此有for有几层嵌套，递归就有几层，在这里就是K是多少就多少次递归。横向就是枚举每个点都有的情况。

这句话仍然抽象，我们图示一下上面我们自己枚举时的过程。

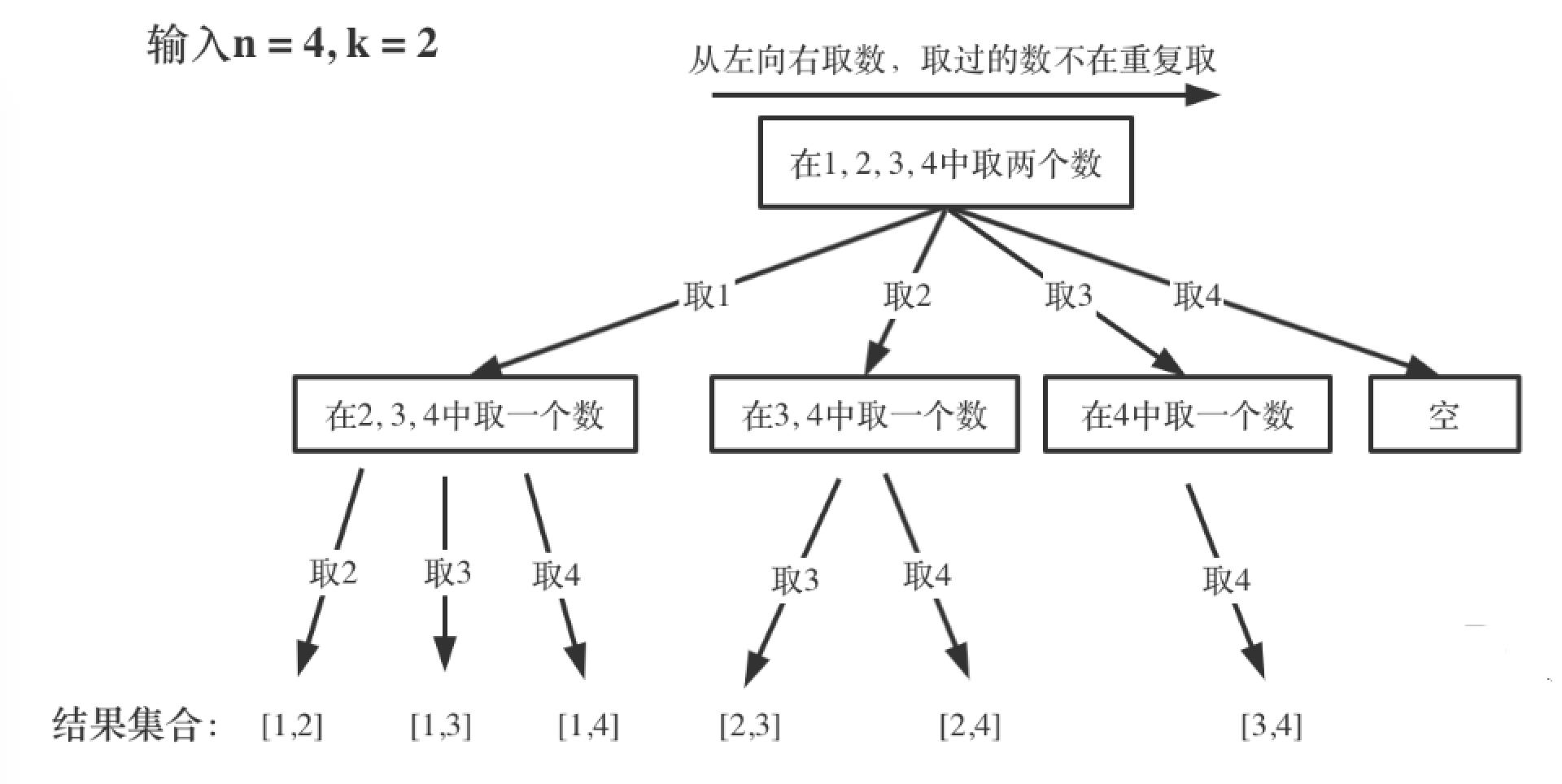
 n=4时，我们可以选择的n有 1,2,3,4这四种情况，所以我们从第一层到第二层的分支有四个，分别表示可以取1，2，3，4。而且这里 从左向右取数，取过的数，不在重复取。 第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。

每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。到了取4时就直接为空了。

那么如何在这个树上遍历，然后收集到我们要的结果集呢? 很显然图中每次搜索到了叶子节点，我们就找到了一个结果。虽然最后一个是空，但是不影响结果。这里相当于只需要把从根节点开始每次选择的内容（分支）达到叶子节点时的结果收集起来，就可以求得 n个数中k个数的组合集合。

从图中可以发现n相当于树的宽度，k相当于树的深度。这里我们就将回溯模型与N叉树建立了联系。

当然这里的树和我们理解的N叉树还有有些区别的，每个元素节点的值不一定是一个。所以递归的完整代码就是如下：

    public List<List<Integer>> combine(int n, int k) 
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) 
            return res;
        
//        用户返回结果
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    

    public void dfs(int n, int k, int startIndex, Deque<Integer> path, List<List<Integer>> res) 
        // 递归终止条件是：path 的长度等于 k
        if (path.size() == k) 
            res.add(new ArrayList<>(path));
            return;
        

        // 针对一个结点，遍历可能的搜索起点，其实就是枚举
        for (int i = startIndex; i <= n; i++) 
            // 向路径变量里添加一个数，就是上图中的一个树枝的值
            path.addLast(i);
            // 搜索起点要加1是为了缩小范围，下一轮递归做准备，因为不允许出现重复的元素
            dfs(n, k, i + 1, path, res);
            // 递归之后需要做相同操作的逆向操作,具体后面继续解释
            path.removeLast();
        
    

这段代码的框架就是遍历N叉树，有两个地方可能比较难理解：

1.startIndex和i是怎么变化的，为什么传给下一层是要加1。

2.后面为什么会有一个回溯的操作 path.removeLast();

我们一个个解释。

4.1深入分析startIndex的变化

我们可以看到在递归里有个循环

 for (int i = startIndex; i <= n; i++) 
    dfs(n,k,i+1,path,res);

这里的循环有什么作用呢？看一下图就知道了，这里其实就是枚举，第一次n=4，可以选择1 ，2，3，4四种情况，所以就有四个分支，for循环就会执行四次：

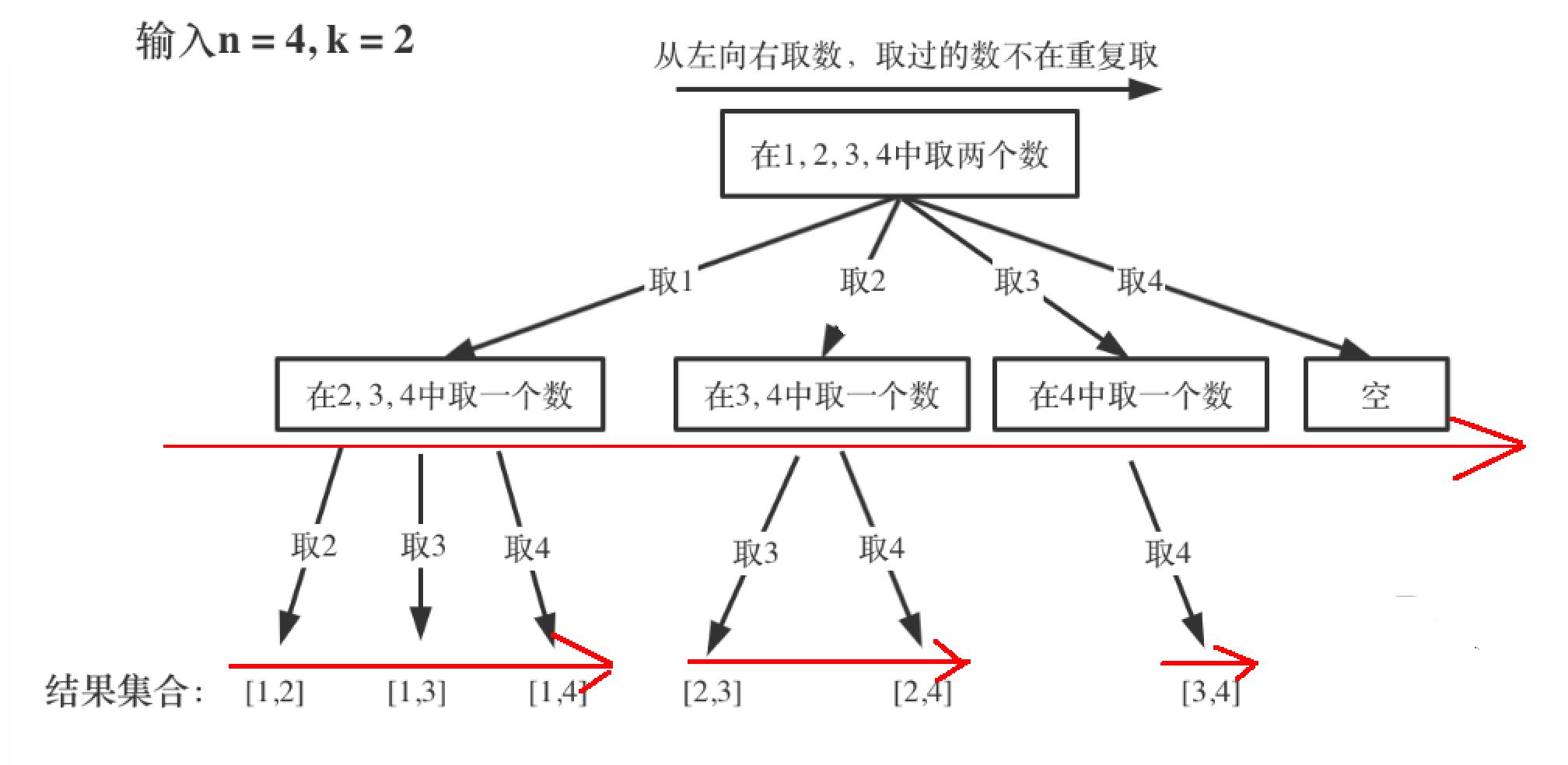
 而对于第二层第一个，选择了1之后，剩下的元素只有2 ，3， 4了，所以这时候for循环就执行3。后面的则只有2次和1次。

那这里为什么第二层的结点数从左向右依次减少，到最后只剩空了呢？这里其实就是我们上面说的暴力过程的前半部分：

如果让我们说过程，就是这样：n=4，那就是所有的数字为1,2,3,4

1. 先取一个1，则有[1,2]，[1,3]，[1,4]三种可能。
2. 然后取一个2，因为1已经取过了，所以不再取，则有[2,3]，[2,4]两种可能。
3. 再取一个3，因为1和2都取过了，所以不再取，则有[3,4]一种可能。
4. 再取4，因为1，2，3都已经取过了，所以直接返回null。

所以说这个for循环解决的就是“横”向宽度的问题。

4.2 为什么有个撤销的操作

回溯最难理解的部分是这个回溯过程：

  path.addLast(i);
  dfs(n, k, i + 1, path, res);
  path.removeLast();

最后为什么要remove这个撤销操作呢？直接说原因，就是当从一个分支跳到另一个分支的时候，如果不把前一个分支的数据给移除掉，那么list就会把前一个分支的数据带到下一个分支去，造成结果错误。具体怎么回事呢？我们可以对照结构图， 用我们拆解递归的方法，将递归拆分成函数调用，会发现输出第一条路径1,2的步骤如下如下：：

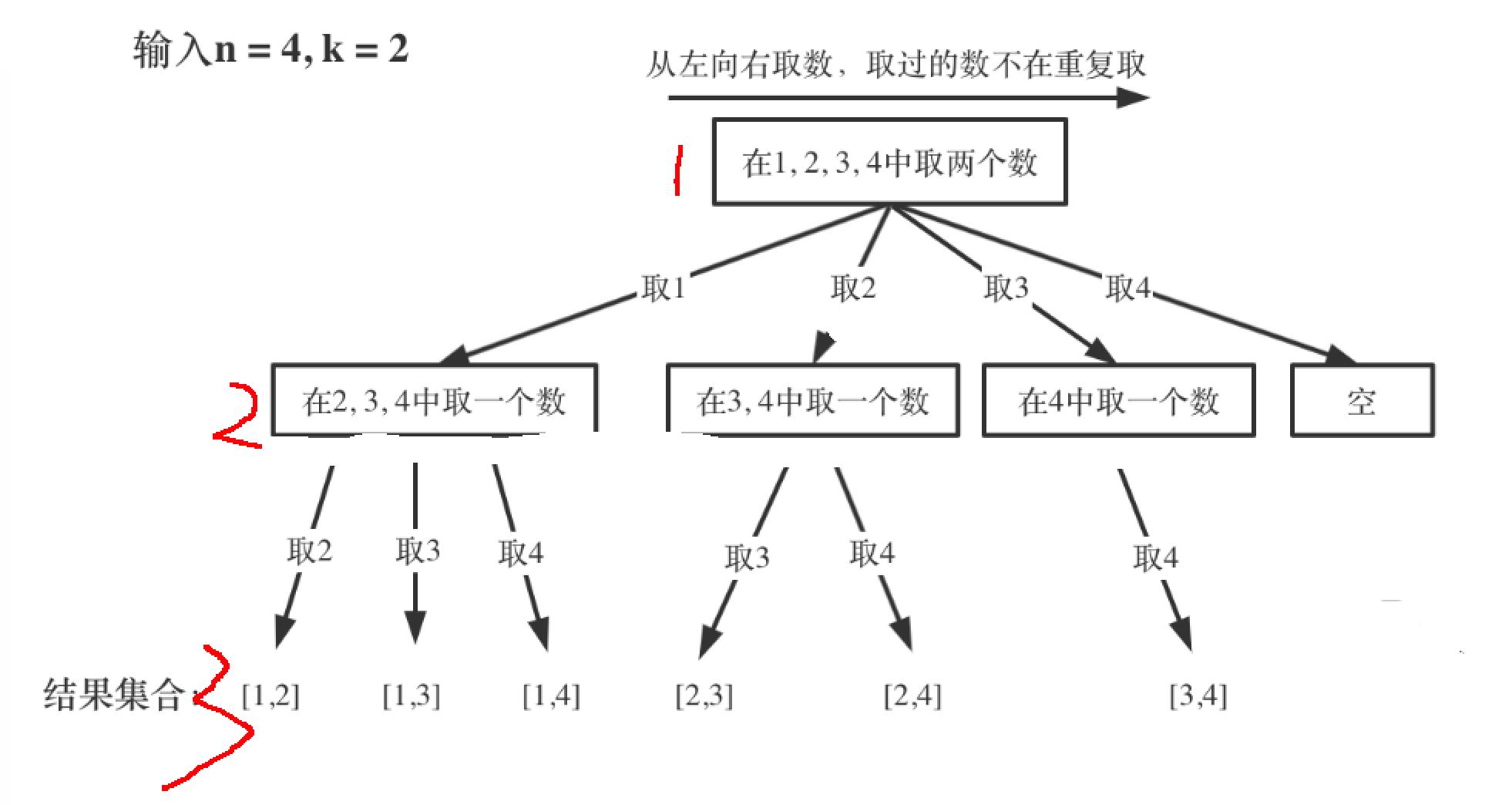
对应的函数执行过程如下

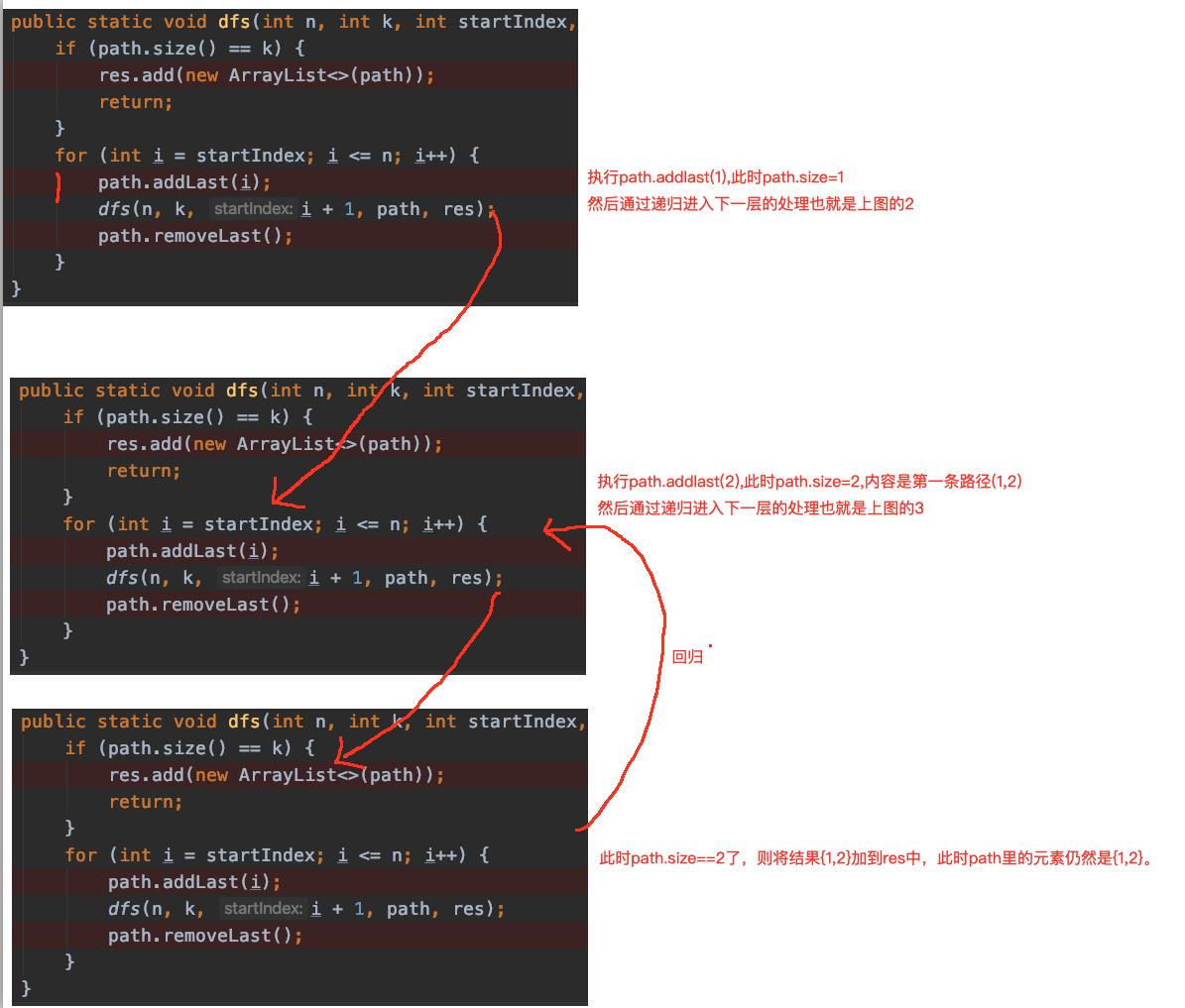
 然后呢？1,2输出 之后会怎么执行呢？回归之后，假如我们将remove代码去掉，也就是这样子：

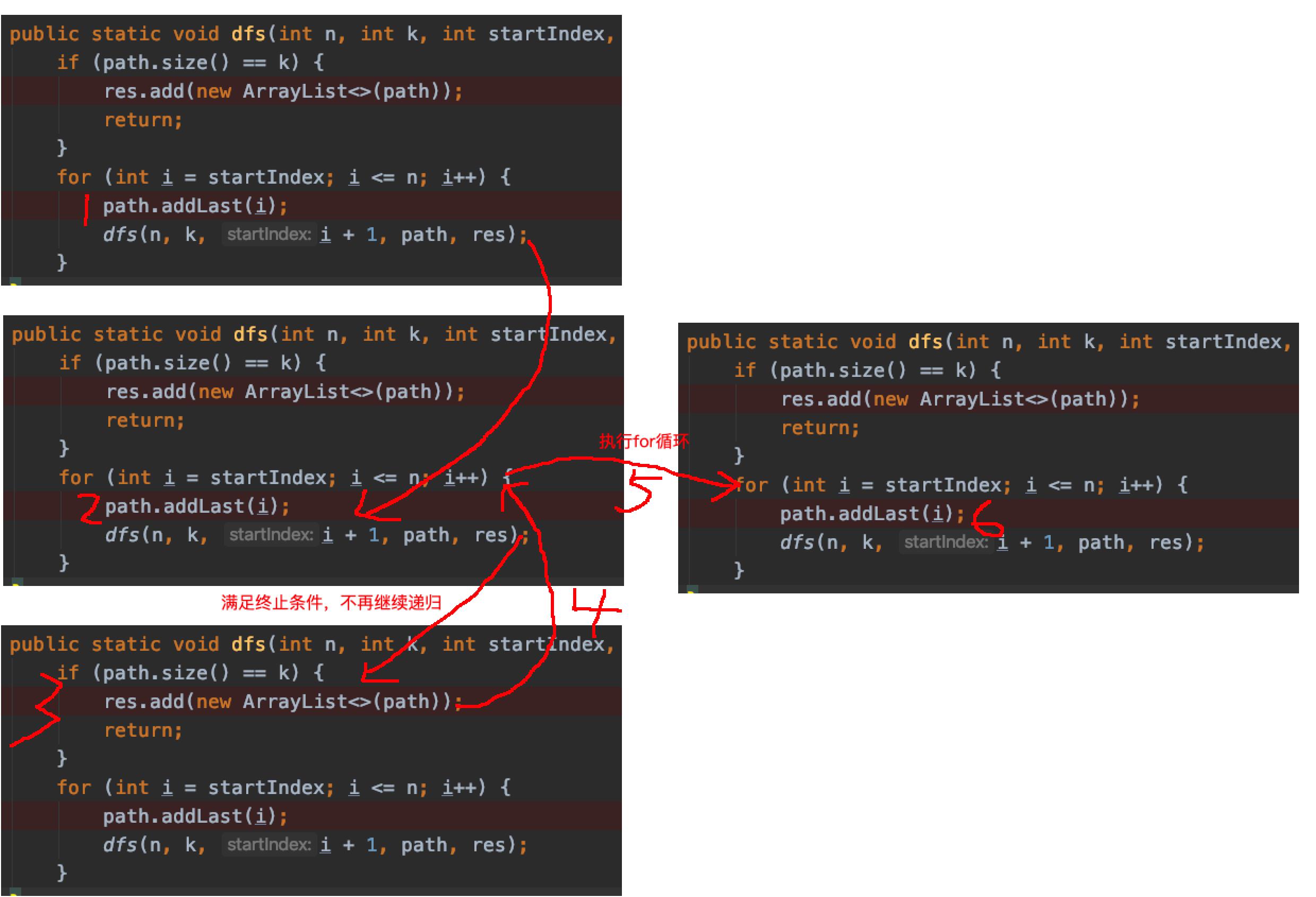
 注意上面的4号位置结束之后会让让一层递归执行for循环体，也就是上面的5。进入5之后，接着开始执行第6步：path.addLast(i)了，此时path的大小是3，元素是1,2,3，为什么会这样呢？

因为path是一个全局的引用，各个递归函数公用的，所以当1,2处理完之后，2污染了path变量。我们希望将1保留而将最后一个2给干掉，然后让3进来，所以这时候需要手动remove一下。

同样3处理完之后，我们也不希望3污染接下来的1,4，1全部走完之后也不希望1污染接下来的2,3等等，这就是为什么回溯里会在递归之后有一个remove撤销操作。