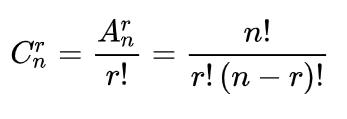2021年软件类第十二届蓝桥杯 省赛 python组 F-J题解

Posted 风信子的猫Redamancy

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了2021年软件类第十二届蓝桥杯 省赛 python组 F-J题解相关的知识，希望对你有一定的参考价值。

2021年软件类第十二届蓝桥杯 省赛 python组 F-J题解

文章目录


备战蓝桥杯的时候，记录一下写的题目和一些思考和理解

这里面的题目都可以从https://www.lanqiao.cn/courses/2786/learning/?id=280833得到，写了一些python的解法
在这一部分之中，我也配套做了一下视频的讲解，如果看题解太干涩，也可以去b站看看视频，这里给出链接B站视频

试题 F:时间显示

题目描述

小蓝要和朋友合作开发一个时间显示的网站。

在服务器上，朋友已经获取了当前的时间，用一个整数表示，值为从 1970 年 1 月 1 日 00:00:00 到当前时刻经过的毫秒数。

现在，小蓝要在客户端显示出这个时间。小蓝不用显示出年月日，只需要显示出时分秒即可，毫秒也不用显示，直接舍去即可。

给定一个用整数表示的时间，请将这个时间对应的时分秒输出。

输入描述

输入一行包含一个整数，表示时间。

输出描述

输出时分秒表示的当前时间，格式形如 HH:MM:SS，其中 HH 表示时，值为 0 到 23，MM 表示分，值为 0 到 59，SS 表示秒，值为 0 到 59。时、分、秒 不足两位时补前导 0。

输入输出样例

示例 1

输入

46800999

输出

13:00:00

示例 2

输入

1618708103123

输出

01:08:23

评测用例规模与约定

对于所有评测用例，给定的时间为不超过 1 0 18 10^18 1018 的正整数。

思路

对于这道题来说，其实也很简单，不过我这里给两种做法

第一种就是计算时间，这就需要我们计算秒，比如一天有24x60x60ms，然后计算天，时，分，秒，然后就可以得出来

第二种就是利用datetime库，那真的是很简单

代码1

# https://www.lanqiao.cn/problems/1452/learning/
t = int(input())
t = t//1000 # 转化为秒s
d = t % (24*60*60) # 得到一天的秒数，因为一天有24*60*60s
hh = d//(3600)  # 得到小时，因为一小时有3600
mm = d%3600//60
ss = d%60
print("%02d:%02d:%02d" % (hh, mm, ss))

代码2（利用datetime库）

# https://www.lanqiao.cn/problems/1452/learning/
import datetime
date = int(input())

start = datetime.datetime(1970,1,1,00,00,00)
timedelta = datetime.timedelta(milliseconds=date)
now = start+timedelta
strf = now.strftime("%H:%M:%S")
print(strf)

试题 G:杨辉三角形

题目描述

下面的图形是著名的杨辉三角形：

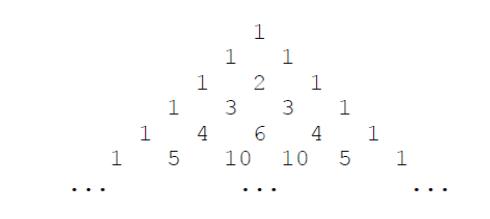
如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列：$ 1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, \\cdots$

给定一个正整数 N，请你输出数列中第一次出现 N 是在第几个数？

输入描述

输入一个整数 N。

输出描述

输出一个整数代表答案。

输入输出样例

示例 1

输入

6

输出

13

评测用例规模与约定

对于 20% 的评测用例， 1 ≤ N ≤ 10 1\\leq N\\leq 10 1≤N≤10； 对于所有评测用例， 1 ≤ N ≤ 1000000000 1\\leq N\\leq 1000000000 1≤N≤1000000000。

思路

实际上呢，这一道题是一道思维题，一开始我也搞不清楚这一道题要什么，后面发现居然是一道规律题。

这道题实在是有些复杂，首先我们就可以用我们的组合数，这个组合数我们也可以直接通过math库里面进行返回，实在不会我们也可以利用数学公式进行求得，也就是一个循环就可以得到。这里说明一下，好像在3.8之前的版本，这个函数是放在itertools里面的，不过现在调用math库即可，因为我们的官方环境是3.8.6

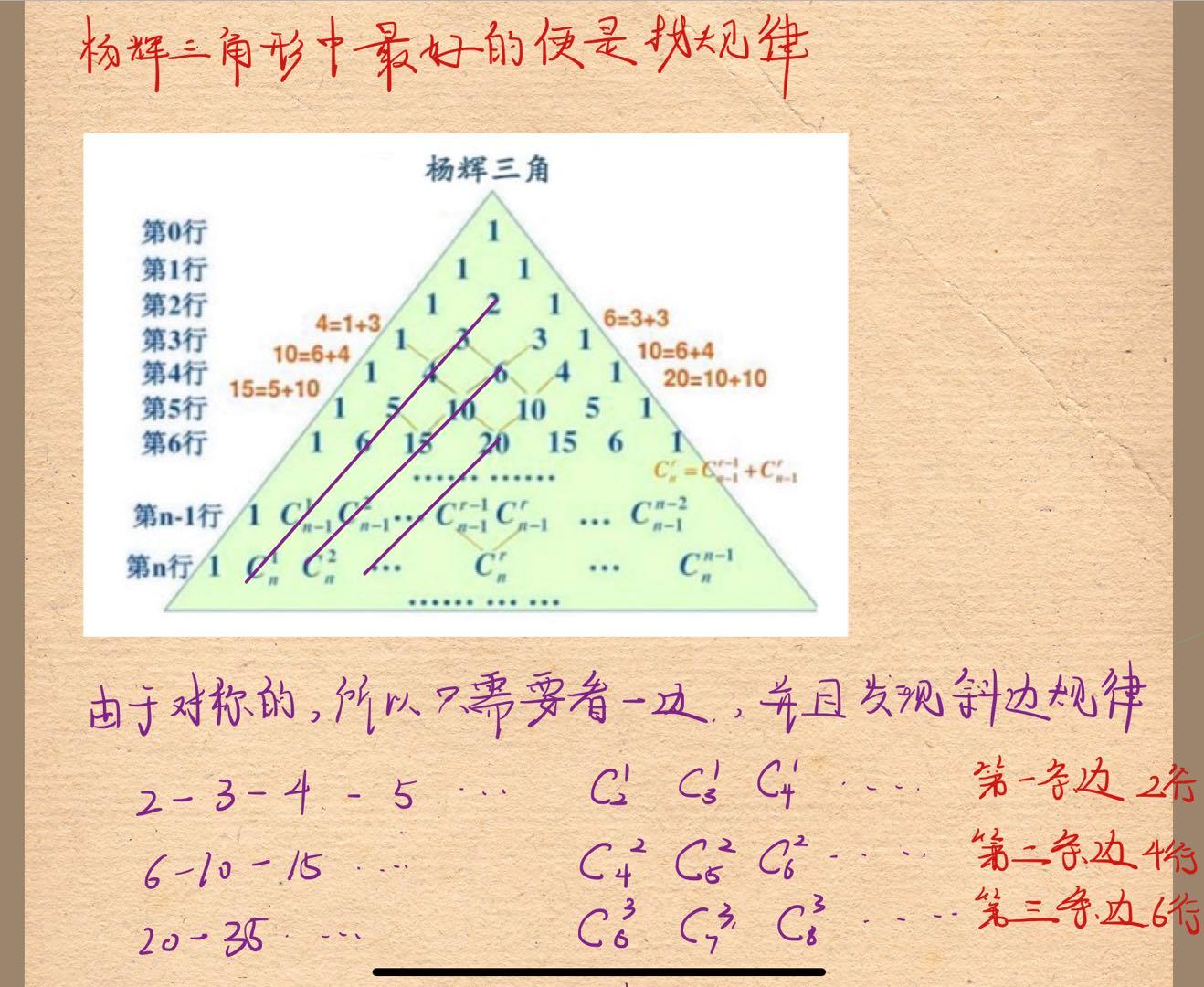
好吧，接下来就介绍一下这道题，我觉得吧，杨辉三角形最好的便是寻找规律，我们可以看到下图，是我做的一个笔记，我们需要看这个斜边，我们可以发现这个斜边实际上是有规律的，由于两边是堆成的，所以我们只需要看一边

我们会发现以上的规律，首先是单调递增的，其次，如果我们得到边的序号x，那我们的L=2x，比如我上面举的例子，第一条便就是2行，第二条边就是4行，第三条边就是6行，所以所有边的第开始的第一个序号就是我们的 C 2 x x C_2x^x C2xx​。

为了找到我们的数，我们就需要二分找到我们的[L，R]的区间，这里要注意的是，斜边上的数，都是出现的第一个数，换句话来说，就是第一次出现的数。

接着我们就需要确立第几个数了，首先我我们可以设 n = C q x n = C_q^x n=Cqx​

我们依旧可以找规律

C 4 2 = 6 − > ( 1 + 2 + 3 + 4 ) + 2 + 1 = 13 C_4^2=6 -> (1+2+3+4) + 2 + 1 = 13 C42​=6−>(1+2+3+4)+2+1=13

C 5 2 = 10 − > ( 1 + 2 + 3 + 4 + 5 ) + 2 + 1 = 18 C_5^2 = 10 -> (1+2+3+4+5) + 2+1=18 C52​=10−>(1+2+3+4+5)+2+1=18

C 7 1 = 7 − > ( 1 + 2 + 3 + 4 + 5 + 6 + 7 ) + 1 + 1 = 30 C_7^1=7->(1+2+3+4+5+6+7)+1+1=30 C71​=7−>(1+2+3+4+5+6+7)+1+1=30

所以总结就是，如果 n = C q x n=C_q^x n=Cqx​，那就就在 ( 1 + 2 + 3 + . . . + q ) + x + 1 = ( q + 1 ) ∗ q / 2 + x + 1 (1+2+3+...+q)+x+1=(q+1)*q/2 + x + 1 (1+2+3+...+q)+x+1=(q+1)∗q/2+x+1个位置

然后我们所说的二分查找就是在不同的斜边来说，查找数，比如说第x条斜边中，我们查找q

代码

# https://www.lanqiao.cn/problems/1457/learning/
n = int(input())
import math
# 求组合数
def C(a, b):
    # return math.comb(a,b) # 可以调用数学库，直接计算
    res = 1
    i = a
    j = 1
    while j <= b:
        res = res * i // j # 分子是b的阶乘，b!
        if res > n: # 组合数是递增的，这时候已经比他大了，直接返回便可
            return res
        i -= 1
        j += 1
    return res

# 二分查找n，由于数字在1000w之内，所以确立一个上界为16
for k in range(16, -1, -1):
    l = 2 * k # 每一个斜边的上的数 L = 2*x
    r = max(n, l) 
    res = -1
    # 二分法寻找
    while l <= r:
        mid = l + r >> 1
        if C(mid, k) >= n: # 如果C(mid,k) >= n
            res = mid 
            r = mid - 1
        else:
            l = mid + 1
    if C(res, k) == n: # 这时候已经找到我们的行数res,和在第k个
        print((res + 1) * res // 2 + k + 1)
        break

试题 H:左孩子右兄弟

题目描述

对于一棵多叉树，我们可以通过 “左孩子右兄弟” 表示法，将其转化成一棵二叉树。

如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。

换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。

给定一棵包含 NN 个结点的多叉树，结点从 1 至 N编号，其中 1 号结点是根，每个结点的父结点的编号比自己的编号小。

请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树，高度最高是多少。

注：只有根结点这一个结点的树高度为 0。

输入描述

输入的第一行包含一个整数 N。 以下 N −1 行，每行包含一个整数，依次表示 2 至 N 号结点的父结点编号。

输出描述

输出一个整数表示答案。

输入输出样例

示例 1

输入

5
1
1
1
2

输出

4

评测用例规模与约定

对于 30 % 30\\% 30%的评测用例， 1 ≤ N ≤ 20 1 \\leq N \\leq 20 1≤N≤20；

对于所有评测用例， 1 ≤ N ≤ 100000 1 \\leq N \\leq 100000 1≤N≤100000。

思路

对于这道题来说，左孩子右兄弟，我们需要达到最深的二叉树，比较简单的来说，就是每次选择孩子更多的作为最后一个结点

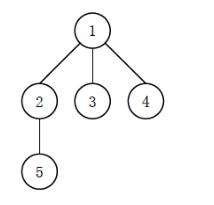
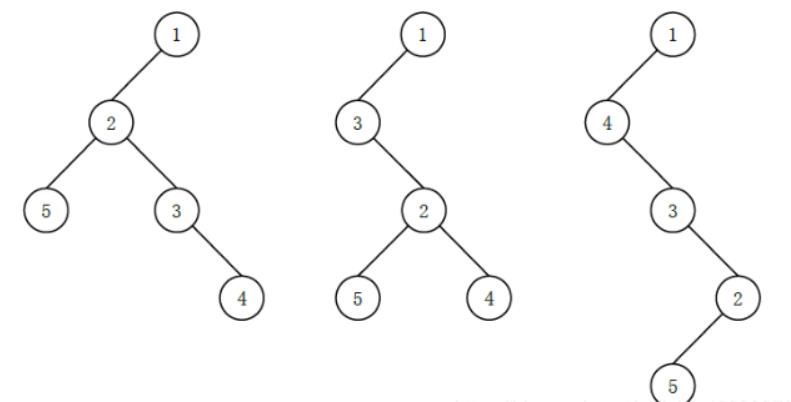
比如对于这样一幅图，我们可以有以下的方法，我列出了其中的三种方法

我们可以看到，最深的就是最后一个，唯一的却别就是2有一个孩子5，所以深度就增加了

好了，简单理清思路我们就可以用我们的dfs了，首先我们可以从输入中创建邻接表，可以判断两个结点是否有联系。

每次的最大深度就是我们孩子数量，然后又加上孩子的孩子的数量，我们就用了深度优先搜索DFS，每次DFS孩子，取最大深度，最后从根，也就是1开始DFS，最后输出dp[1]就是我们的结果。

dp[u]：以点 u 为根节点，通过 “左孩子右兄弟” 表示法转化成二叉树后的最大高度；

dp[u] = 子节点数量 + 子树转化为二叉树后的最大高度

代码

# https://www.lanqiao.cn/problems/1451/learning/
import sys
# 树形DP
g = [[] for j in range(1, 100100)] # 邻接表
dp = [0] * 100100

# 设置递归深度
sys.setrecursionlimit(150000)

def dfs(u):
    dp[u] = len(g[u]) # 全部变为左孩子，那么长度就是孩子的数量
    maxv = 0
    for v in g[u]:
        dfs(v) # DFS孩子
        maxv = max(dp[v], maxv) # 取最大深度
    dp[u] += maxv # 每次加上最大深度

n = int(input())
for i in range(2, n + 1):
    v = int(input())
    g[v].append(i)
dfs(1)
print(dp[1])

试题 I:异或数列

题目描述

Alice 和 Bob 正在玩一个异或数列的游戏。初始时，Alice 和 Bob 分别有一个整数 a 和 b，初始值均为 0。

有一个给定的长度为 n 的公共数列 X 1 , X 2 , ⋯   , X n X_1, X_2,\\cdots , Xn X1​,X2​,⋯,Xn。Alice 和 Bob 轮流操作，Alice 先手，每步可以在以下两种选项中选一种：

选项 1：从数列中选一个 X i X_i Xi​ 给 Alice 的数异或上，或者说令 a 变为 a ⊕ X i a \\oplus X_i a⊕Xi​。（其中 ⊕ \\oplus ⊕表示按位异或）

选项 2：从数列中选一个 X i X_i Xi​ 给 Bob 的数异或上，或者说令 b 变为 b ⊕ X i b \\oplus X_i b⊕Xi​。

每个数 X i X_i Xi​ 都只能用一次，当所有 X i X_i Xi​以上是关于2021年软件类第十二届蓝桥杯 省赛 python组 F-J题解的主要内容，如果未能解决你的问题，请参考以下文章

2021年软件类第十二届蓝桥杯第二场省赛 python组 F-J题解

2021年软件类第十二届蓝桥杯第二场省赛 python组 A-E题解

2021软件类第十二届蓝桥杯国赛真题 Python组 A-E题解

2021 第十二届蓝桥杯大赛软件赛省赛（第二场），C/C++大学B组题解

2021 第十二届蓝桥杯大赛软件赛省赛（第二场），C/C++大学B组题解

2021.5.9 第十二届蓝桥杯大赛软件赛省赛第二场大学B组（个人题解）