STBCAlamouti，STBC误码率仿真

Posted 2022-03-23 fpga&matlab

%该程序使用的是Alamouti Scheme: [x1 x2;-x2* x1*] R = 3/4
 
%NOTES:
%About entering matrix O:
%-- O is Tp*Nt matrix,as default 4*3 complex orthogonal is defined (rate 3/4).
%for [x1 -x2 -x3;x2* x1* 0;x3* 0 x1*;0 -x3* x2*] -----enter------> O=[1 -2 -3;2+j 1+j 0;3+j 0 1+j;0 -3+j 2+j];
%-- Alamouti Scheme: [x1 x2;-x2* x1*] -----enter------> O=[1 2;-2+j 1+j];
%-- A real orthogonal: [x1 x2;-x2 x1] -----enter------> O=[1 2;-2 1];
%-- For real orthogonal matrices define M_psk=2; as real signal constellation.
%-- O=[1]; is uncoded (no diversity).
%-- In this program entries of O cannot be like "a1*x1[*]+a2*x2[*]+...+an*xn[*]" only they can be like "x1 or -x1 or x1* or -x1*".
%------------------------------------------------------------------------
clear all
O=[1 -2 -3;2+j 1+j 0;3+j 0 1+j;0 -3+j 2+j];                          %Complex or Real Orthogonal Matrix **define this**  
Nt=size(O,2);                                                        %Number of Transmit antennas
co_time=size(O,1);                                                   %Block time length
Nr=1;                                                                %Number of Receive antennas        **define this**
Nit=100000;                                                          %Number of repeates for each snr   **define this**
M_psk=4;                                                             %M-PSK  constellation,M_psk=2^k    **define this**
snr_min=3;                                                           %Min snr range for simulation      **define this**
snr_max=15;                                                          %Max snr rande for simulation      **define this**
graph_inf_bit=zeros(snr_max-snr_min+1,2);                            %Plot information
graph_inf_sym=zeros(snr_max-snr_min+1,2);                            %Plot information
num_X=1;
num_bit_per_sym=log2(M_psk);
for cc_ro=1:co_time
    for cc_co=1:Nt
        num_X=max(num_X,abs(real(O(cc_ro,cc_co))));
    end
end
co_x=zeros(num_X,1);
for con_ro=1:co_time                                                 %Compute delta,epsilon,eta and conj matrices
    for con_co=1:Nt
        if abs(real(O(con_ro,con_co)))~=0
            delta(con_ro,abs(real(O(con_ro,con_co))))=sign(real(O(con_ro,con_co)));
            epsilon(con_ro,abs(real(O(con_ro,con_co))))=con_co;
            co_x(abs(real(O(con_ro,con_co))),1)=co_x(abs(real(O(con_ro,con_co))),1)+1;
            eta(abs(real(O(con_ro,con_co))),co_x(abs(real(O(con_ro,con_co))),1))=con_ro;
            coj_mt(con_ro,abs(real(O(con_ro,con_co))))=imag(O(con_ro,con_co));
        end
    end
end
eta=eta.';                                                           %Sort is not necessary
eta=sort(eta);
eta=eta.';
for SNR=snr_min:snr_max                                              %Start simulation
    clc
    disp('Wait until SNR=');disp(snr_max);
    SNR
    n_err_sym=0;
    n_err_bit=0;
    graph_inf_sym(SNR-snr_min+1,1)=SNR;
    graph_inf_bit(SNR-snr_min+1,1)=SNR;
    for con_sym=1:Nit
        bi_data=round(rand(num_X,num_bit_per_sym)>=0.5);                      %Random binary data
        de_data=bi2de(bi_data);                                      %Convert binary data to decimal for use in M-PSK mod.
        data=pskmod(de_data,M_psk,0,'gray');
        H=randn(Nt,Nr)+j*randn(Nt,Nr);                               %Path gains matrix 
        XX=zeros(co_time,Nt);
        for con_r=1:co_time                                          %Start space time coding
            for con_c=1:Nt
                if abs(real(O(con_r,con_c)))~=0
                    if imag(O(con_r,con_c))==0
                        XX(con_r,con_c)=data(abs(real(O(con_r,con_c))),1)*sign(real(O(con_r,con_c)));
                    else
                        XX(con_r,con_c)=conj(data(abs(real(O(con_r,con_c))),1))*sign(real(O(con_r,con_c)));
                    end
                end
            end
        end                                                          %End space time coding
        H=H.';
        XX=XX.';
        snr=10^(SNR/10);
        Noise=(randn(Nr,co_time)+j*randn(Nr,co_time));               %Generate Noise
        Y=(sqrt(snr/Nt)*H*XX+Noise).';                               %Received signal
        H=H.';                                                       %Start decoding with perfect channel estimation
        for co_ii=1:num_X
            for co_tt=1:size(eta,2)
                if eta(co_ii,co_tt)~=0
                    if coj_mt(eta(co_ii,co_tt),co_ii)==0
                        r_til(eta(co_ii,co_tt),:,co_ii)=Y(eta(co_ii,co_tt),:);
                        a_til(eta(co_ii,co_tt),:,co_ii)=conj(H(epsilon(eta(co_ii,co_tt),co_ii),:));
                    else
                        r_til(eta(co_ii,co_tt),:,co_ii)=conj(Y(eta(co_ii,co_tt),:));
                        a_til(eta(co_ii,co_tt),:,co_ii)=H(epsilon(eta(co_ii,co_tt),co_ii),:);
                    end
                end
            end
        end
        RR=zeros(num_X,1);
        for ii=1:num_X                                               %Generate decision statistics for the transmitted signal "xi"
            for tt=1:size(eta,2)
                for jj=1:Nr
                    if eta(ii,tt)~=0
                        RR(ii,1)=RR(ii,1)+r_til(eta(ii,tt),jj,ii)*a_til(eta(ii,tt),jj,ii)*delta(eta(ii,tt),ii);
                    end
                end
            end
        end
        re_met_sym=pskdemod(RR,M_psk,0,'gray');                      % = ML decision for M-PSK
        re_met_bit=de2bi(re_met_sym);
        re_met_bit(1,num_bit_per_sym+1)=0;                           %For correct demension of "re_met_bit"
        for con_dec_ro=1:num_X                                             
            if re_met_sym(con_dec_ro,1)~=de_data(con_dec_ro,1)
                n_err_sym=n_err_sym+1;
                for con_dec_co=1:num_bit_per_sym
                    if re_met_bit(con_dec_ro,con_dec_co)~=bi_data(con_dec_ro,con_dec_co)
                        n_err_bit=n_err_bit+1;
                    end
                end
            end
        end
    end
    Perr_sym=n_err_sym/(num_X*Nit);                                  %Count number of error bits and symbols 
    graph_inf_sym(SNR-snr_min+1,2)=Perr_sym;
    Perr_bit=n_err_bit/(num_X*Nit*num_bit_per_sym);
    graph_inf_bit(SNR-snr_min+1,2)=Perr_bit;
end
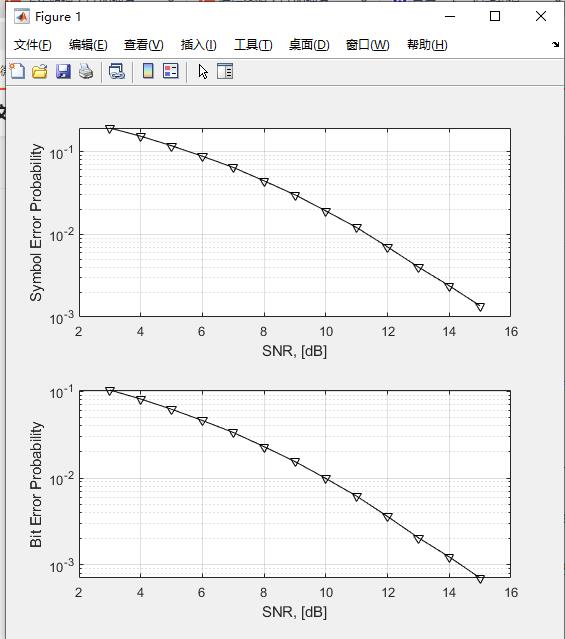
x_sym=graph_inf_sym(:,1);                                            %Generate plot
y_sym=graph_inf_sym(:,2);
subplot(2,1,1);
semilogy(x_sym,y_sym,'k-v');
xlabel('SNR, [dB]');
ylabel('Symbol Error Probability');
grid on
x_bit=graph_inf_bit(:,1);
y_bit=graph_inf_bit(:,2);
subplot(2,1,2);
semilogy(x_bit,y_bit,'k-v');
xlabel('SNR, [dB]');
ylabel('Bit Error Probability');
grid on