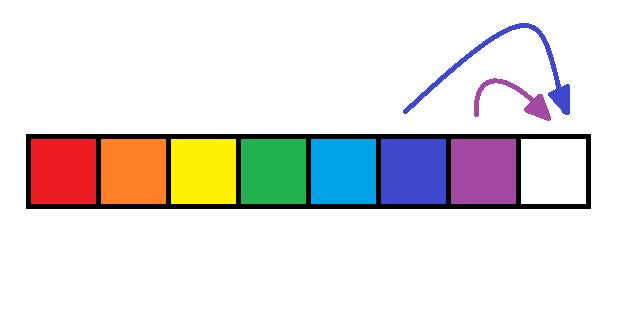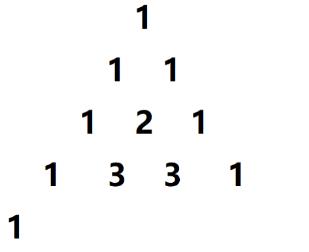C语言每日一练 —— 第22天:动态规划
Posted 英雄哪里出来
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C语言每日一练 —— 第22天:动态规划相关的知识,希望对你有一定的参考价值。
前言
很多人加我都是想询问如何学好算法。我的方法是我用了 十年 的时间,自己总结出来的,不可能适合所有人,但是我觉得挺有效的,如果你觉得可行,尽管一试!
首先,我们心中要有一团🔥火🔥,一团希望之🔥火🔥!只要你心中充满希望,即使是死去的意志也会在你内心复活。
「 动态规划 」作为算法中一块比较野的内容,没有比较系统的分类,只能通过不断总结归纳,对各种类型进行归类。「 动态规划 」(即 Dynamic programming,简称 DP)是一种在数学、管理科学、计算机科学 以及 生物信息学中使用的,通过把原问题分解为相对简单的「 子问题 」的方式求解「 复杂问题 」的方法。
「 动态规划 」是一种算法思想:若要解一个给定问题,我们需要解其不同部分(即「 子问题 」),再根据「 子问题 」的解以得出原问题的解。要理解动态规划,就要理解 「 最优子结构 」 和 「 重复子问题 」。
本文将针对以下一些常用的动态规划问题,进行由浅入深的系统性讲解。首先来看一个简单的分类,也是今天本文要讲的内容。

文章目录
一、递推问题
递推问题作为动态规划的基础,是最好掌握的,也是必须掌握的,它有点类似于高中数学中的数列,通过 前几项的值 推导出 当前项的值。
1、一维递推
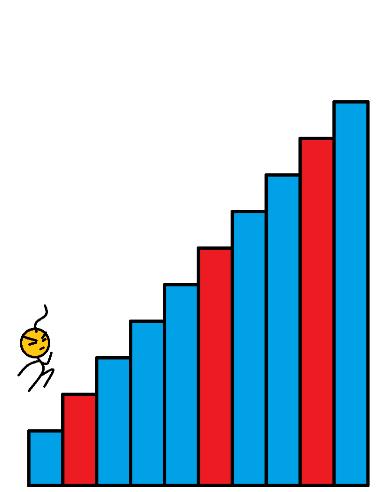
你正在爬楼梯,需要 n n n 阶你才能到达楼顶。每次你可以爬 1 1 1 或 2 2 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
假设我们已经到了第
n
n
n 阶楼梯,那么它可以是从
n
−
1
n-1
n−1 阶过来的,也可以是从
n
−
2
n-2
n−2 阶过来的(但是,不可能是从
n
−
3
n-3
n−3 阶直接过来的),所以如果达到第
n
n
n 阶的方案数为
f
[
n
]
f[n]
f[n],那么到达
n
−
1
n-1
n−1 阶就是
f
[
n
−
1
]
f[n-1]
f[n−1],到达
n
−
2
n-2
n−2 阶 就是
f
[
n
−
2
]
f[n-2]
f[n−2],所以可以得出:
f
[
n
]
=
f
[
n
−
1
]
+
f
[
n
−
2
]
f[n] = f[n-1] + f[n-2]
f[n]=f[n−1]+f[n−2] 其中,当
n
=
0
n=0
n=0 时方案数为 1,代表初始情况;
n
=
1
n=1
n=1 时方案数为 1,代表走了一步,递推计算即可。
以上就是最简单的动态规划问题,也是一个经典的数列:斐波那契数列 的求解方式。它通过一个递推公式,将原本指数级的问题转化成了线性的,时间复杂度为
O
(
n
)
O(n)
O(n)。
C语言代码实现如下:
int f[1000];
int climbStairs(int n)
f[0] = f[1] = 1;
for(int i = 2; i <= n; ++i)
f[i] = f[i-1] + f[i-2];
return f[n];
2、二维递推
给定一个非负整数 n n n,生成杨辉三角的前 n n n 行。在杨辉三角中,每个数是它 左上方 和 右上方 的数的和。
根据杨辉三角的定义,我们可以简单将上面的图进行一个变形,得到:

于是,我们可以得出以下结论:
1)杨辉三角的所有数可以存储在一个二维数组中,行代表第一维,列代表第二维度;
2)第
i
i
i 行的元素个数为
i
i
i 个;
3)第
i
i
i 行 第
j
j
j 列的元素满足公式:
c
[
i
]
[
j
]
=
1
i
=
0
c
[
i
−
1
]
[
j
−
1
]
+
c
[
i
−
1
]
[
j
]
o
t
h
e
r
w
i
s
e
c[i][j] = \\begincases 1 & i=0\\\\ c[i-1][j-1] + c[i-1][j] & otherwise \\endcases
c[i][j]=1c[i−1][j−1]+c[i−1][j]i=0otherwise
于是就可以两层循环枚举了。时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)。
C语言代码实现如下:
int c[40];
void generate(int n)
for(int i = 0; i < n; ++i)
for(int j = 0; j <= i; ++j)
if(j == 0 || j == i)
c[i][j] = 1;
else
c[i][j] = c[i-1][j-1] + c[i-1][j];
二、线性DP
1、最小花费
数组的每个下标作为一个阶梯,第 i i i 个阶梯对应着一个非负数的体力花费值 c o s t [ i ] cost[i] cost[i](下标从 0 开始)。每当爬上一个阶梯,都要花费对应的体力值,一旦支付了相应的体力值,就可以选择 向上爬一个阶梯 或者 爬两个阶梯。求找出达到楼层顶部的最低花费。在开始时,可以选择从下标为 0 0 0 或 1 1 1 的元素作为初始阶梯。
令走到第
i
i
i 层的最小消耗为
f
[
i
]
f[i]
f[i]。假设当前的位置在
i
i
i 层楼梯,那么只可能从
i
−
1
i-1
i−1 层过来,或者
i
−
2
i-2
i−2 层过来;
如果从
i
−
1
i-1
i−1 层过来,则需要消耗体力值:
f
[
i
−
1
]
+
c
o
s
t
[
i
−
1
]
f[i-1] + cost[i-1]
f[i−1]+cost[i−1];
如果从
i
−
2
i-2
i−2 层过来,则需要消耗体力值:
f
[
i
−
2
]
+
c
o
s
t
[
i
−
2
]
f[i-2] + cost[i-2]
f[i−2]+cost[i−2];
起点可以在第 0 或者 第 1 层,于是有状态转移方程:
f
[
i
]
=
0
i
=
0
,
1
min
(
f
[
i
−
1
]
+
c
o
s
t
[
i
−
1
]
,
f
[
i
−
2
]
+
c
o
s
t
[
i
−
2
]
)
i
>
1
f[i] = \\begincases 0 & i=0,1\\\\ \\min ( f[i-1] + cost[i-1], f[i-2] + cost[i-2] ) & i > 1\\endcases
f[i]=0min(f[i−1]+cost[i−1],f[i−2]+cost[i−2])i=0,1i>1

这个问题和一开始的递推问题的区别在于:一个是求前两项的和,一个是求最小值。这里就涉及到了动态取舍的问题,也就是动态规划的思想。
如果从前往后思考,每次都有两种选择,时间复杂度为
O
(
2
n
)
O(2^n)
O(2n)。转化成动态规划以后,只需要一个循环,时间复杂度为
O
(
n
)
O(n)
O(n)。
C语言代码实现如下:
int f[1024];
int min(int a, int b)
return a < b ? a : b;
int minCostClimbingStairs(int* cost, int costSize)
f[0] = 0;
f[1] = 0;
for(int i = 2; i <= costSize; ++i)
f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2]);
return f[costSize];
2、最大子段和
给定一个整数数组 n u m s nums nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
由于要求的是连续的子数组,所以对于第
i
i
i 个元素,状态转移一定是从
i
−
1
i-1
i−1 个元素转移过来的。基于这一点,可以令
f
[
i
]
f[i]
f[i] 表示以
i
i
i 号元素结尾的最大值。
那么很自然,这个最大值必然包含
n
u
m
s
[
i
]
nums[i]
nums[i] 这个元素,那么要不要包含
n
u
m
s
[
i
−
1
]
,
n
u
m
s
[
i
−
2
]
,
n
u
m
s
[
i
−
3
]
,
.
.
.
,
n
u
m
s
[
k
]
nums[i-1],nums[i-2],nums[i-3],...,nums[k]
nums[i−1],nums[i−2],nums[i−3],...,nums[k] 呢?其实就是看第
i
−
1
i-1
i−