[机器学习与scikit-learn-28]:算法-回归-评估指标详解
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[机器学习与scikit-learn-28]:算法-回归-评估指标详解相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123546987
目录
第1章 最小二乘的误差公式
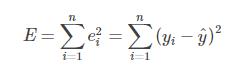
最小二乘法也可以叫做最小平方和,其目的就是通过最小化该误差的平方和,使得拟合对象或拟合函数无限接近目标对象。
这个函数也可以用于机器学习的loss损失函数。
第2章 残差和与MAE
2.1 残差与残差和
最小二乘是误差函数,是一个表达式,是一种表达误差的方法。
在评估指标里,定义了专门的名词来表达误差。
“残差”蕴含了有关模型基本假设的重要信息。
如果回归模型正确的话, 我们可以将残差看作误差的观测值。
它应符合模型的假设条件,且具有误差的一些性质。
利用残差所提供的信息,来考察模型假设的合理性及数据的可靠性称为残差分析。
残差:Yi - Y的绝对值
残差和:所有样本的点的残差的绝对值和。
2.2 绝对均值误差MAE (L1误差)
MAE (Mean absolute error):均值绝对误差或绝对均值误差。
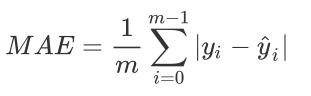
MAE是目标值和预测值之差的绝对值之和的平均。
其只衡量了预测值误差的平均模长,而不考虑方向,
第3章 残差平方和与MSE
3.1 残差平方和RSS
SSE(Sum of Sqaured Error,误差平方和)
RSS(Residual Sum of Squares 残差平方和)
它们都表示所有样本的残差的和。
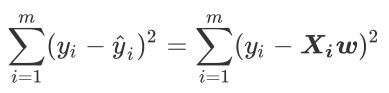
这与最小二乘的表达式一致的。
RSS残差平方和,它的本质是我们的所有预测值与所有真实值之间的差异的累计和。
它是从第一种最小二乘的角度来评估我们回归的效果的,
所以RSS既是我们的损失函数,也是我们回归类模型的模型评估指标之一。
但是,RSS有着致命的缺点:
(1)它是一个无界的和,可以无限地大
样本数越多,该值越大。
(2)不同样本数量之间无法通过RSS进行比较
这是因为RSS是所有样本的残差的累计和
(3)无最小值边界
我们只知道,我们想要求解最小的RSS,从RSS的公式来看,它不能为负,所以RSS越接近0越好,但我们没有一个概念,究竟多小才算好,多接近0才算好?且随着样本数的增加,该最小值也在增加。
3.2 均方误差MSE(L2误差)
为了应对上述状况,经常使用RSS的变体,均方误差MSE(mean squared error)来衡量我们的预测值和真实值的差异。
MSE(mean squared error):均方误差 = RSS/样本数, 是平均残差值。
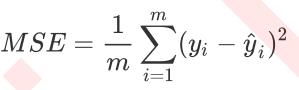
均方误差,本质是在RSS的基础上除以了样本总量,得到了每个样本量上的平均误差。
有了平均误差,我们就可以将平均误差和我们的标签的取值范围在一起比较,以此获得一个较为可靠的评估依据。
有了平均误差MSE,误差的比较就与样本总数无关了。
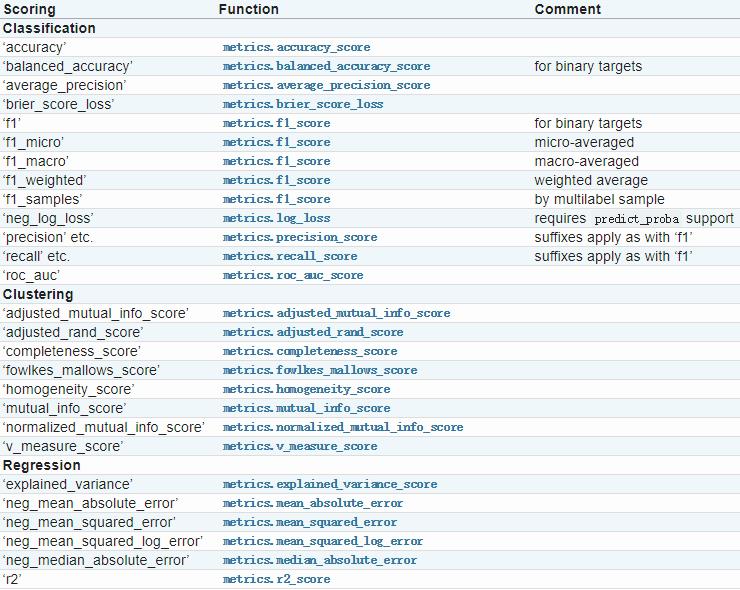
3.3 交叉验证评估指标
第4章 范数与误差
(1)范数的定义
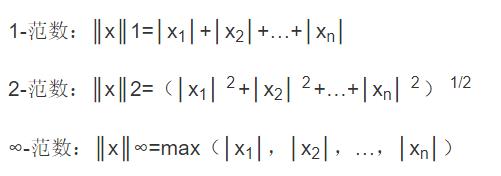
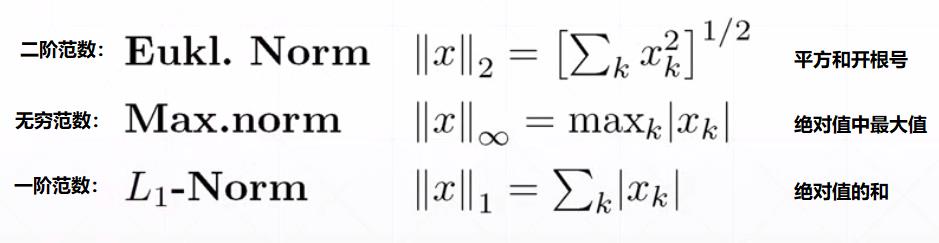
(2)误差与范数
MAE与残差和:属于一范数。
MSE与RSS: 严格意义上讲,还不完全属于二范数,因为二范数不需要平方,且RSS和MSE都没有开根号,粗略讲,可以认为MSE与RSS属于L2范数。
第5章 R^2指标
5.1 MSE和MAE不足
(1)平均误差屏蔽了局部的偏差过大
MSE和MAE属于平均误差,平均误差屏蔽了局部的偏差过大的情形。
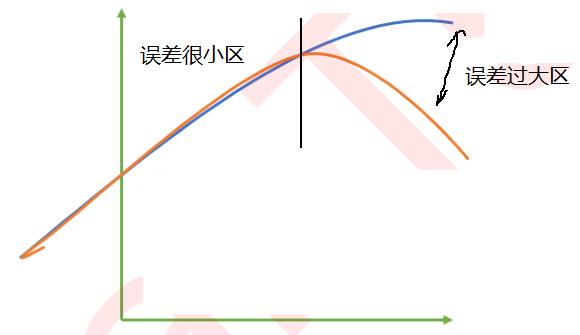
上述图示展示,平均误差可能很小,但在误差过大区,误差太大。
MSE和MAE是累加和,是加法运算,误差大和误差小的值,是同等权重,没有放大,也没有缩小,且采用累加后之后的平均,比如样本数是1000,即使误差较大,经过平均后,误差值会被缩小1000倍,因此最终的误差值,无法体现这种局部异常。
因此,我们需要一种方式,把这种局部异常进行放大。
(2)不同样本+不同模型之间无法比较
MSE和MAE都是平均指标都属于绝对误差,而不是相对误差, 这些误差值并不一定小于1,是可以大于1的,它适应于相同样本,不同模型之间的比较。无法适用于不同样本,不同于模型之间的比较。因此,我们需要一种相对误差来表达模型的预测效果
5.2 决定系数R2指标

分子:反应的是模型的预测值与样本标签值之间的误差。
分母:反应的是模型的预测值与均值之间的误差,反应的发散程度。
根据 R-Squared 的取值,来判断模型的好坏,其取值范围为[0,1]:
随着样本数量的增加,分子分母都同时增加,因此,他们是相对指标,不是绝对指标。
一般来说,R-Squared 越大,R越接近1, 表示模型拟合效果越好。
一般来说,R-Squared 越小, R越接近0, 表示模型拟合效果越差。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123546987
以上是关于[机器学习与scikit-learn-28]:算法-回归-评估指标详解的主要内容,如果未能解决你的问题,请参考以下文章