AI数学基础26-卷积（Convolution）

Posted 2023-03-23

参考技术A 卷积（Convolution）是一个应用非常广泛的函数间的数学运算，类似加、减、乘、除。之所以很多同学听到卷积二字就头皮发麻，是因为不熟悉，而且在日常生活中用的少。加、减、乘、除从小就学习，天天在使用，所以觉得简单、容易，亲切。

加、减、乘、除 用符号 +，-，×，÷，表示；同样，卷积用符号：* 表示。

如上所述，卷积是两个函数之间的数学运算，假设有两个函数f(t), g(t)，其卷积运算的结果也是函数，我们记做c(t)，则：

c(t) = f(t)*g(t) = (f*g)(t)

注意：f(t)*g(t)和(f*g)(t)这两种写法，都是表示卷积运算，大家在学习一个数学运算的时候， 首先是要学习并熟悉其标记的含义 ，这跟学习加、减、乘、除一样。

卷积具体的计算是如何定义的呢？

两个函数f(t), g(t)是定义在实数范围内可积的函数，其卷积记作：f*g，是其中一个函数翻转并平移后与另一个函数的乘积的积分，如下图所示：

咋一看，有点儿懂了，也有点儿没懂，不着急，接下来我们一步一步图解卷积运算的过程。

首先 ，已知两函数f(t)和g(t)，如下图所示

然后 ，根据上述的卷积运算定义，把两个函数f(t)和g(t)自变量由t换为τ，并把其中一个函数，比如g(τ)，向右移动t个单位，得到g(τ-t)。

接着 ，把右移t个单位的函数，以纵轴为中心，180°翻转（Flip）,得到g(-(τ-t))，即g(t-τ)，如下图所示：

这样，经过平移和翻转，我们得到了积分表达式中的f(τ）和g(t-τ)。

接下来 ，τ是自变量，对整个定义域，我们对f(τ）和g(t-τ)积分，如下图所示：

最后 ，完成f(τ）和g(t-τ)的积分运算后，就完成了两个函数f(t)和g(t)的卷积运算。

通过上述演示过程，大家可以把两个函数的卷积运算，简单记住为：“ 卷积就是平移翻转再积分 ”，其过程如下图所示：

若把g(t-τ)看作为是一个加权函数的话，卷积可以认为是对f(τ)取加权值的过程。

跟加、减、乘、除有交换律，结合律相似，卷积也有如下性质

卷积定理 指出，函数卷积的 傅里叶变换 是函数傅里叶变换的乘积。即，一个域中的卷积相当于另一个域中的乘积，例如 时域 中的卷积就对应于 频域 中的乘积。

这一定理对 拉普拉斯变换 、 双边拉普拉斯变换 、 Z变换 、 Mellin变换 和 Hartley变换 （参见 Mellin inversion theorem ）等各种傅里叶变换的变体同样成立。利用卷积定理可以简化卷积的运算量。对于长度为 n 的序列，按照卷积的定义进行计算，需要做 2n-1 组对位乘法，其 计算复杂度 为O(n²)；而利用 傅里叶变换 将序列变换到频域上后，只需要一组对位乘法，利用傅里叶变换的 快速算法 之后，总的计算复杂度为O(n·log(n))。卷积定理简化运算在工程实现中，经常使用。

卷积在科学、工程和数学上都有很多应用 ：

代数 中，整数乘法和多项式乘法都是卷积。

图像处理 中，用作图像模糊、锐化、 边缘检测 。

统计学 中，加权的滑动平均是一种卷积。

概率论 中，两个统计独立变量X与Y的和的 概率密度函数 是X与Y的概率密度函数的卷积。

声学 中， 回声 可以用源声与一个反映各种反射效应的函数的卷积表示。

电子工程 与信号处理中，任一个线性系统的输出都可以通过将输入信号与系统函数（系统的 冲激响应 ）做卷积获得。

物理学 中，任何一个线性系统（符合 叠加原理 ）都存在卷积。

下一节将继续介绍《 AI数学基础27-离散卷积（Discrete convolution） 》

卷积运算(convolution)基础

一、向量的卷积运算

---

 

给定两个n维向量α=(a₀, a₁, ..., a_n-1)^T，β=(b₀, b₁, ..., b_n-1)^T，则α与β的卷积运算定义为：

α*β=(c₀, c₁, ..., c_2n-2)^T，其中

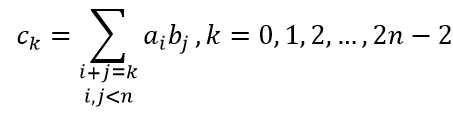
事实上，“卷积”的含义从矩阵αβ^T的表示即可以看出：不难发现，c_k即为第k列副对角线元素之和。形象地讲，对α与β作卷积，就像是将由α与β的元素形成的下述矩阵“面”沿副对角线方向卷了起来得到的“一束”向量。

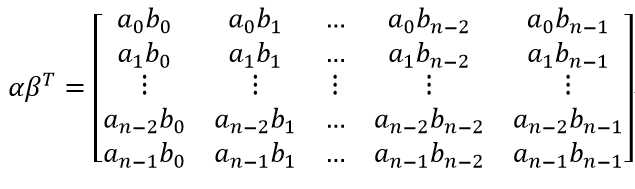
卷积的蛮力算法的时间复杂度为O(n²)。为提高算法效率，可以用插值法，这将在下一篇博文有关快速傅立叶变换的内容中予以介绍。

二、卷积应用

---

2.1 多项式乘法

卷积运算与多项式乘法是对应的。不难验证，设多项式f(x)=a₀+a₁x+a₂x²+...+a_m-1x^m-1, g(x)=b₀+b₁x+b₂x²+...+b_n-1x^n-1，则f(x)g(x)得到的多项式的系数列向量就刚好是对f(x)与g(x)的系数列向量的卷积运算的结果。

2.2 信号平滑处理

由于噪声干扰，信号往往需要进行平滑处理。

设信号向量为α=(a₀, a₁, ..., a_m-1)，权向量β=(b_2k, b_2k-1, ..., b₀)=(w_-k, ..., w_k)。一个比较常用的权向量的例子是高斯滤波权值向量，其中

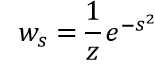
这里z用于归一化处理。

运用权向量β与信号向量α的卷积，我们可以实现为信号去噪，得到向量γ=(a‘₀, a‘₁, ..., a‘_m-1)，其中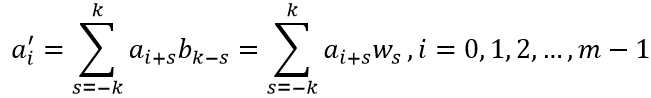

不过，对于边界上的元素，由于缺项无法对齐，经过运算后可能存在误差。