人工势场法路径规划算法（APF）

Posted 2023-03-23 慕羽★

   本文主要对人工势场法路径规划算法进行介绍，主要涉及人工势场法的简介、引力和斥力模型及其推导过程、人工势场法的缺陷及改进思路、人工势场法的Python与MATLAB开源源码等方面

   一、人工势场法简介

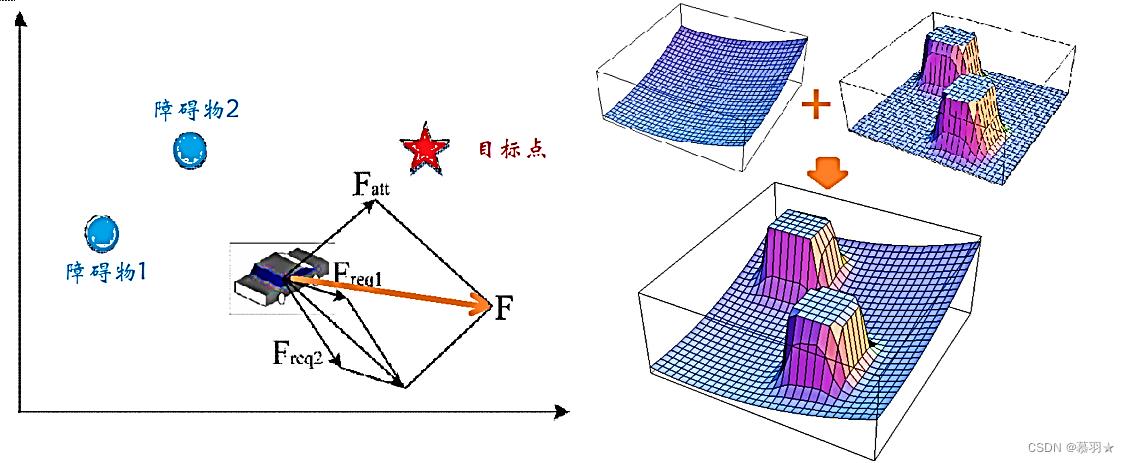
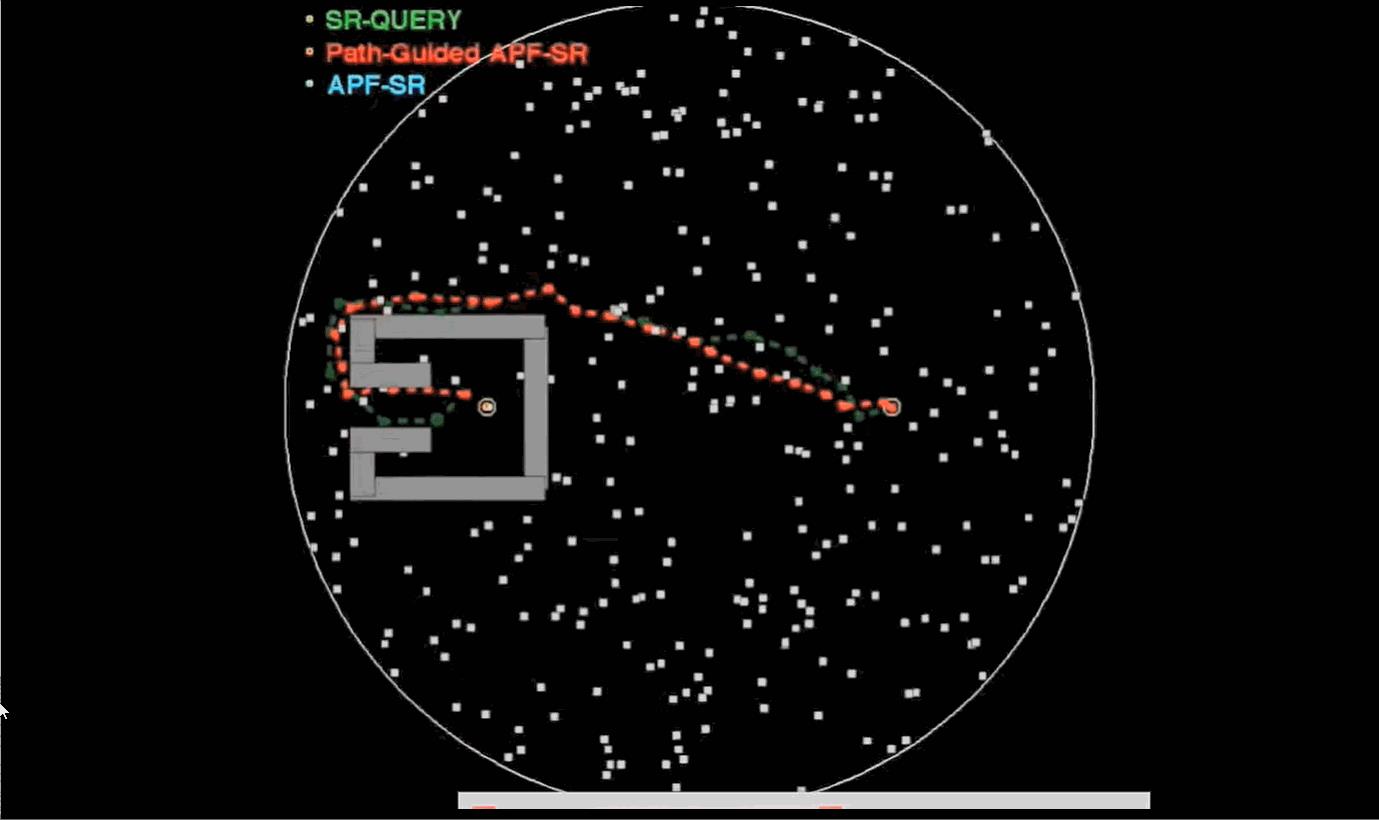
   人工势场法是由Khatib于1985年在论文《Real-Time Obstacle Avoidance for Manipulators and Mobile Robots》中提出的一种虚拟力法。它的基本思想是将机器人在周围环境中的运动，设计成一种抽象的人造引力场中的运动，目标点对移动机器人产生“引力”，障碍物对移动机器人产生“斥力”，最后通过求合力来控制移动机器人的运动。应用势场法规划出来的路径一般是比较平滑并且安全，但是这种方法存在局部最优点问题。

---

   二、引力与斥力模型及公式推导

   1、基础知识补充：梯度

   梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

---

   2、引力与斥力模型

   引力势场主要与机器人和目标点间的距离有关，距离越大，机器人所受的势能值就越大;距离越小，机器人所受的势能值则越小，所以引力势场的函数为:

   $$U_{att}\left(q\right)=\frac{1}{2}\eta {\rho }^2\left(q,q_g\right)$$

   其中η为正比例增益系数，ρ(q,qg)为一个矢量，表示机器人的位置q和目标点位置qg之间的欧几里德距离|q-qg|。矢量方向是从机器人的位置指向目标点位
置。

   相应的引力$F_{att}\left(X\right)$为引力场的负梯度:

   $$F_{att}\left(X\right)=-\nabla U_{att}\left(X\right)=\eta \rho \left(q,q_g\right)$$

   决定障碍物斥力势场的因素是机器人与障碍物间的距离，当机器人未进入障碍物的影响范围时，其受到的势能值为零;在机器人进入障碍物的影响范围后，两者之间的距离越大,机器人受到的斥力就越小，距离越小，机器人受到的斥力就越大,斥力势场的势场函数为：

   $$U_{r{e}_1}(X)=\{\begin{array}{ll}\frac{1}{2}k(\frac{1}{\rho (q,q_o)}-\frac{1}{{\rho }_o}{)}^2& 0\le \rho (q,q_o)\le {\rho }_o\\ 0& \rho (q,q_o)\ge {\rho }_o\end{array}$$

   其中k为正比例系数，ρ(q,qo)为一矢量，方向为从障碍物指向机器人，大小为机器人与障碍物间的距离|q-qo|，ρo为一常数，表示障碍物对机器人产生作用的最大距离。相应的斥力为斥力场的负梯度:

   $$F_{n_0}(X)=\{\begin{array}{ll}k(\frac{1}{\rho (q,q_0)}-\frac{1}{{\rho }_0})\frac{1}{{\rho }^2(q,q_0)}\nabla \rho (q,q_0)& 0\le \rho (q,q_0)\le {\rho }_0\\ 0& \rho (q,q_0)\ge {\rho }_0\end{array}$$

   其中$\begin{array}{r}\nabla \rho (q,q_0)\end{array}$表示从$q_0$指向q的单位向量

   $$\nabla \rho (q,q_0)=\frac{q-q_0}{\Vert q-q_0\Vert }$$

---

   3、引力与斥力公式的推导过程

   设机器人位置为(x, y)，障碍物位置为(xg, yg)，则引力势场函数可由下式

   $$U_{att}\left(q\right)=\frac{1}{2}\eta {\rho }^2(q,q_g)$$

   改写为：

   U a t t ( x , y ) = 1 2 η [ ( x − x g ) 2 + ( y − y g ) 2 ] U_a t t\\big(x,y\\big)=\\frac12\\eta\\biggl[\\bigl(x-x_g\\bigr)^2+\\bigl(y-y_g\\bigr)^2\\biggr]

路径规划基于matlab改进的人工势场算法机器人避障路径规划含Matlab源码 1151期

一、简介

人工势场法是局部路径规划的一种比较常用的方法。这种方法假设机器人在一种虚拟力场下运动。

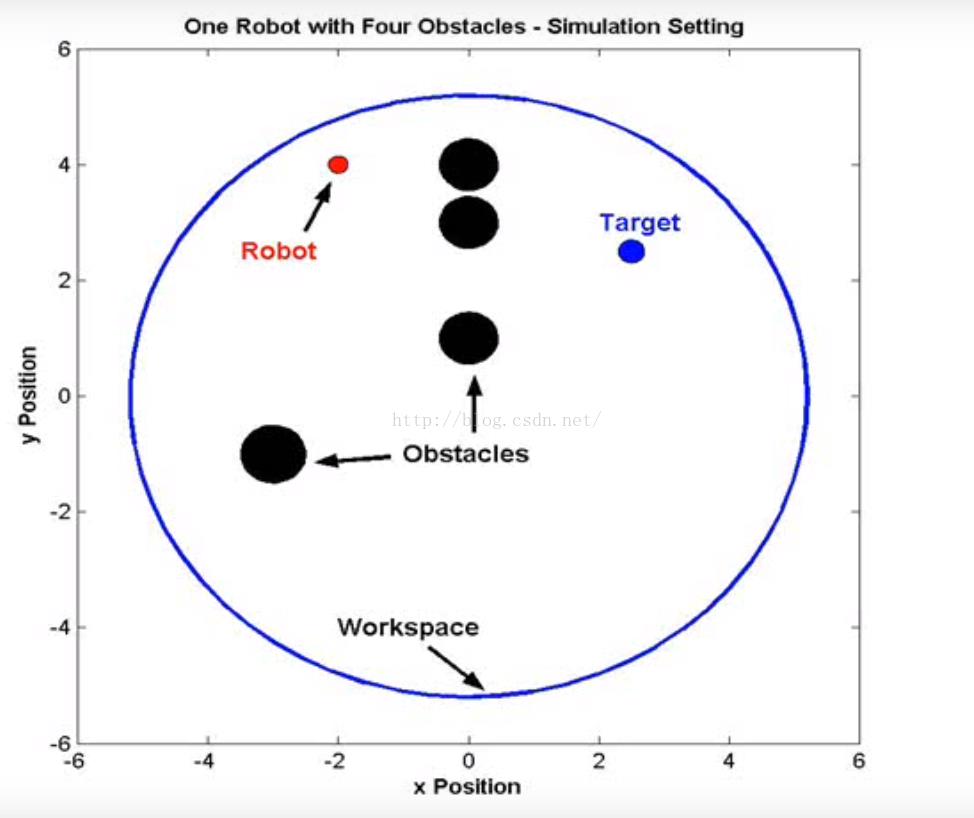
如图所示，机器人在一个二维环境下运动，图中指出了机器人，障碍和目标之间的相对位置。

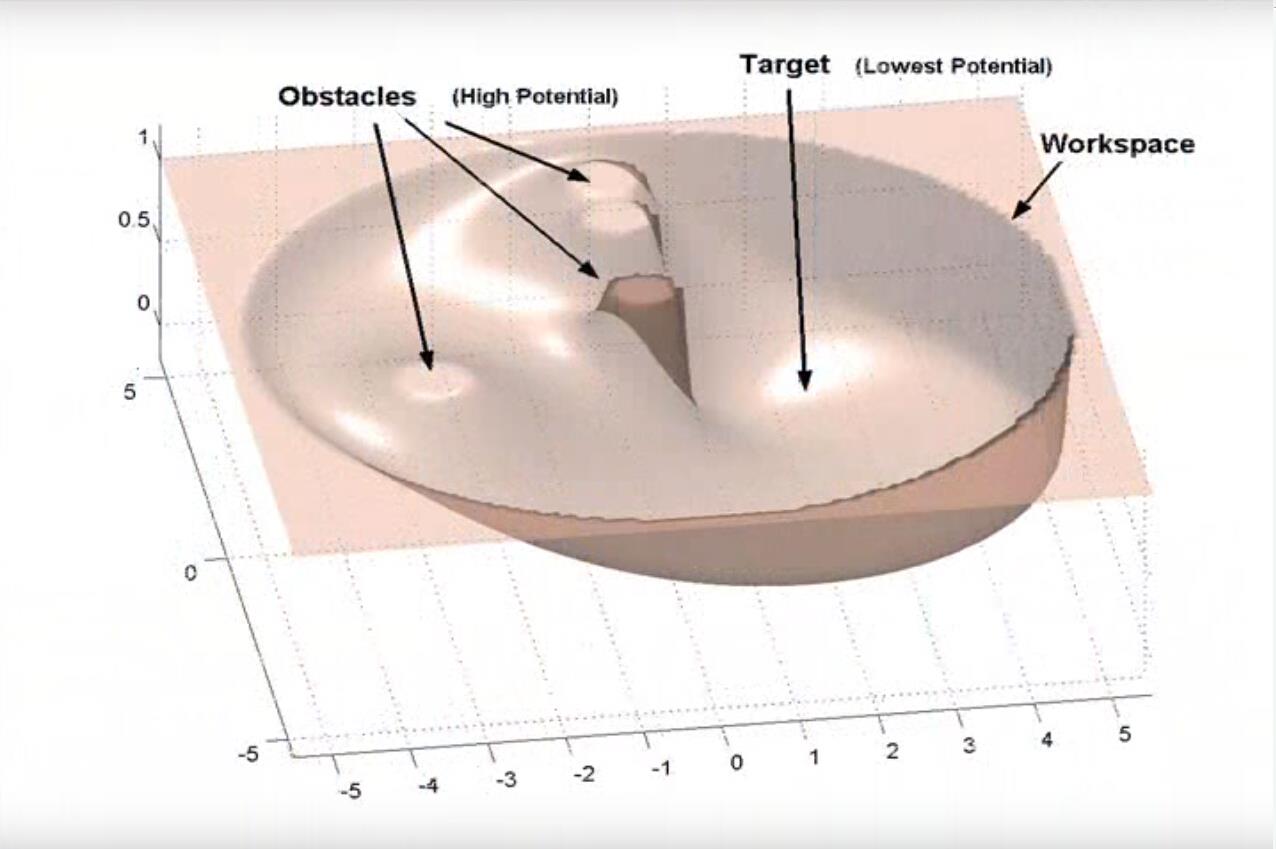
这个图比较清晰的说明了人工势场法的作用，物体的初始点在一个较高的“山头”上，要到达的目标点在“山脚”下，这就形成了一种势场，物体在这种势的引导下，避开障碍物，到达目标点。

人工势场包括引力场合斥力场，其中目标点对物体产生引力，引导物体朝向其运动（这一点有点类似于A*算法中的启发函数h）。障碍物对物体产生斥力，避免物体与之发生碰撞。物体在路径上每一点所受的合力等于这一点所有斥力和引力的和。这里的关键是如何构建引力场和斥力场。下面我们分别讨论一下：

引力场：

常用的引力函数：

这里的ε是尺度因子.ρ(q,q_goal)表示物体当前状态与目标的距离。引力场有了，那么引力就是引力场对距离的导数（类比物理里面W=FX）：、

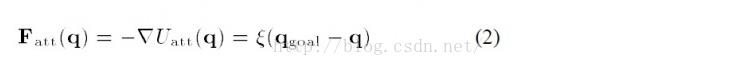
关于梯度的算法可以参考相关资料，简单提一下，二元函数梯度是酱紫的[δx,δy],这个符号是偏导数，不太对，见谅。

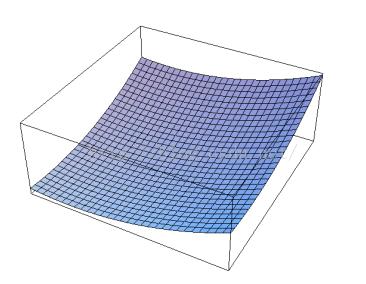
Fig .引力场模型

斥力场：

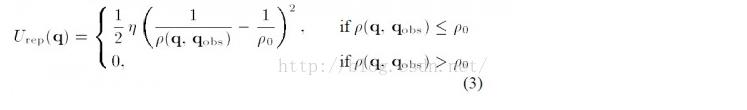
公式（3）是传统的斥力场公式，现在还没有搞清楚是怎么推导出来的。公式中η是斥力尺度因子，ρ（q,q_obs）代表物体和障碍物之间的距离。ρ_0代表每个障碍物的影响半径。换言之，离开一定的距离，障碍物就对物体没有斥力影响。

斥力就是斥力场的梯度


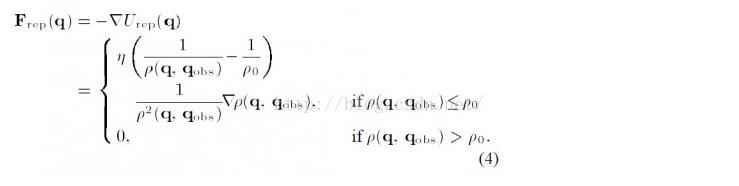
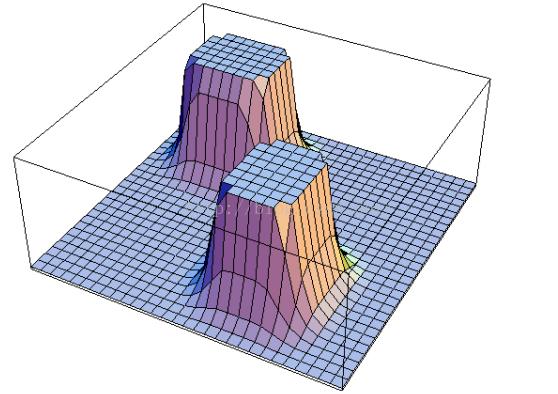
Fig 斥力场模型

总的场就是斥力场合引力场的叠加，也就是U=U_att+U_rep,总的力也是对对应的分力的叠加，如下图所示：

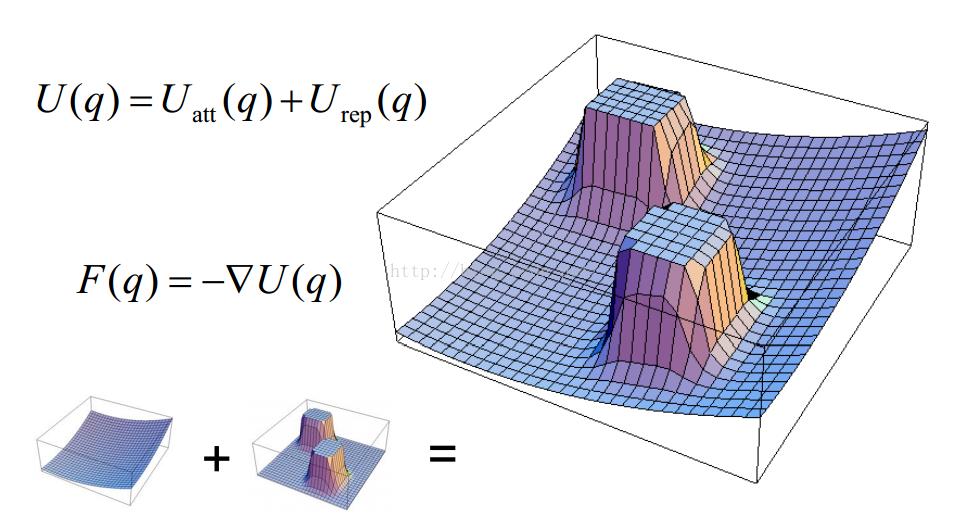
二、存在的问题
（a） 当物体离目标点比较远时，引力将变的特别大，相对较小的斥力在甚至可以忽略的情况下，物体路径上可能会碰到障碍物

（b）当目标点附近有障碍物时，斥力将非常大，引力相对较小，物体很难到达目标点

（c）在某个点，引力和斥力刚好大小相等，方向想反，则物体容易陷入局部最优解或震荡

三、各种改进版本的人工势场法
（a）对于可能会碰到障碍物的问题，可以通过修正引力函数来解决，避免由于离目标点太远导致引力过大

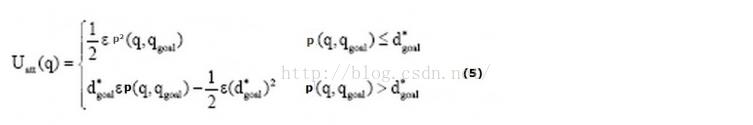
和（1）式相比，（5）式增加了范围限定。d*_goal 给定了一个阈值限定了目标和物体之间的距离。对应的梯度也就是引力相应变成：

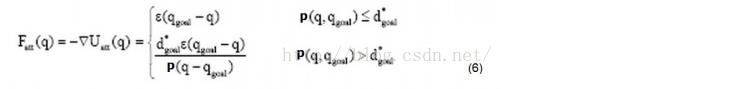
（b）目标点附近有障碍物导致目标不可达的问题，引入一种新的斥力函数

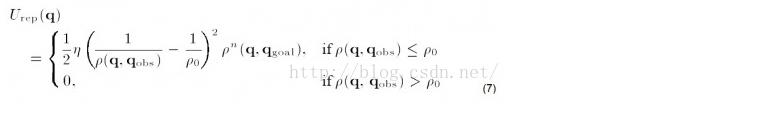
这里在原有斥力场的基础上，加上了目标和物体距离的影响,（n是正数，我看到有篇文献上n=2）。直观上来说，物体靠近目标时，虽然斥力场要增大，但是距离在减少，所以在一定程度上可以起到对斥力场的拖拽作用

相应斥力变成：

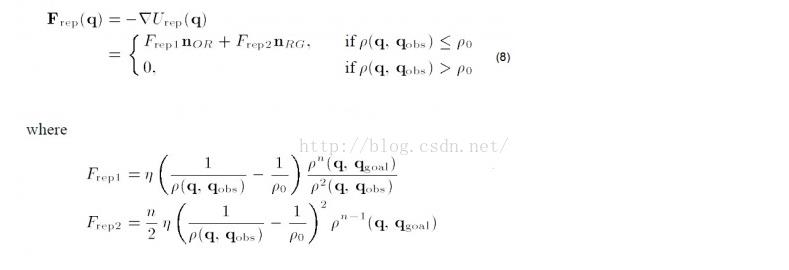
所以可以看到这里引力分为两个部分，编程时要格外注意

（c）局部最优问题是一个人工势场法的一个大问题，这里可以通过加一个随机扰动，让物体跳出局部最优值。类似于梯度下降法局部最优值的解决方案。

二、源代码

clear all;
%障碍和目标，起始位置都已知的路径规划,意图实现从起点可以规划出一条避开障碍到达目标的路径。
%初始化车的参数
Xo=[0 0];% 起点位置
k=1000;% 计算引力需要的增益系数
%K=0;% 初始化
m=10;% 计算斥力的增益系数，都是自己设定的。
Po=1;%障碍影响距离，当障碍和车的距离大于这个距离时，斥力为0，即不受该障碍的影响。也是自己设定。
n=9;%障碍个数
a=0.5;
l=0.1;% 步长
J=300;%循环迭代次数
r = 0.5;
%如果不能实现预期目标，可能也与初始的增益系数， Po 设置的不合适有关。
%end
%给出障碍和目标信息
Xsum=[10 10;1 1.5;3 2.2;4 4.5;3 6;6 2.5;5.5 6; 6 4.5;9 9;8.5 5];% 这个向量是(n+1)*2 维，其中[10 10] 是目标位置，剩下的都是障碍的位置。
Xj=Xo;%j=1 循环初始，将车的起始坐标赋给Xj
%*************** 初始化结束，开始主体循环******************
for j=1:J% 循环开始
    Goal(j,1)=Xj(1);%Goal 是保存车走过的每个点的坐标。刚开始先将起点放进该向量。
    Goal(j,2)=Xj(2);
    %调用计算角度模块
    Theta=compute_angle(Xj,Xsum,n);%Theta 是计算出来的车和障碍，和目标之间的与X 轴之间的夹角，统一规定角度为逆时针方向，用这个模块可以计算出来。
    %调用计算引力模块
    Angle=Theta(1);%Theta （1）是车和目标之间的角度，目标对车是引力。
    angle_at=Theta(1);% 为了后续计算斥力在引力方向的分量赋值给angle_at
    [Fatx,Faty]=compute_Attract(Xj,Xsum,k,Angle,0,Po,n);% 计算出目标对车的引力在x,y 方向的两个分量值。
    for i=1:n
        angle_re(i)=Theta(i+1);% 计算斥力用的角度，是个向量，因为有n 个障碍，就有n 个角度。
    end
    %调用计算斥力模块
    [Frerxx,Freryy,Fataxx,Fatayy]=compute_repulsion(Xj,Xsum,m,angle_at,angle_re,n,Po,a,r);%计算出斥力在x,y 方向的分量数组。
    %计算合力和方向，这有问题，应该是数，每个j 循环的时候合力的大小应该是一个唯一的数，不是数组。应该把斥力的所有分量相加，引力所有分量相加。
    Fsumyj=Faty+Freryy+Fatayy;%y 方向的合力
    Fsumxj=Fatx+Frerxx+Fataxx;%x 方向的合力
    Position_angle(j)=atan(Fsumyj/Fsumxj);% 合力与x 轴方向的夹角向量
    %计算车的下一步位置
   
    %保存车的每一个位置在向量中
    Xj=Xnext;
    %判断
    if ((Xj(1)-Xsum(1,1))>0)&((Xj(2)-Xsum(1,2))>0)% 是应该完全相等的时候算作到达， 还是只是接近就可以？现在按完全相等的时候编程。
        K=j  % 记录迭代到多少次，到达目标。
    break;
    %记录此时的j 值
    end%如果不符合if 的条件，重新返回循环，继续执行。
end%大循环结束
K=j;
Goal(K,1)=Xsum(1,1);% 把路径向量的最后一个点赋值为目标
Goal(K,2)=Xsum(1,2);
%*********************************** 画出障碍， 起点， 目标， 路径点*************************
%画出路径
 
%路径向量Goal 是二维数组,X,Y 分别是数组的x,y 元素的集合，是两个一维数组。
x=[1 3 4 3 6 5.5 6  9 8.5];% 障碍的x 坐标
y=[1.5 2.2 4.5 6 2.5 6 4.5 9 5];
plot(10,10,'v',0,0,'ms',X,Y ,'-k','linewidth',3);

Pathkm = K*l
%斥力计算
function [Yrerxx,Yreryy,Yataxx,Yatayy]=compute_repulsion(X,Xsum,m,angle_at,angle_re,n,Po,a,r)% 输入参数为当前坐标， Xsum 是目标和障碍的坐标向量，增益常数,障碍，目标方向的角度
Rat=(X(1)-Xsum(1,1))^2+(X(2)-Xsum(1,2))^2;% 路径点和目标的距离平方
rat=sqrt(Rat);% 路径点和目标的距离
for i=1:n
    Rrei(i)=(X(1)-Xsum(i+1,1))^2+(X(2)-Xsum(i+1,2))^2;% 路径点和障碍的距离平方
    rre(i)=sqrt(Rrei(i))-r;% 路径点和障碍的距离保存在数组rrei 中
    R0=(Xsum(1,1)-Xsum(i+1,1))^2+(Xsum(1,2)-Xsum(i+1,2))^2;
    r0=sqrt(R0)-r;
    if rre(i)>Po% 如果每个障碍和路径的距离大于障碍影响距离，斥力令为0
        Yrerx(i)=0;
        Yrery(i)=0;
        Yatax(i)=0;
        Yatay(i)=0;
    else
%if r0<Po
       if rre(i)<Po/2
           if X(2)>Xsum(i+1,2)
               Yrer(i)=m*(1/rre(i)-1/Po)*((1/rre(i))^2)*(rat);% 分解的Fre1 向量
               Yata(i)=a*m*((1/rre(i)-1/Po)^2)*(rat^a);% 分解的Fre2 向量
               Yrerx(i)=-Yrer(i)*cos(angle_re(i));%angle_re(i)=Y(i+1)
               Yrery(i)=1*Yrer(i)*sin(angle_re(i));
               Yatax(i)=Yata(i)*cos(angle_at);%angle_at=Y(1)
               Yatay(i)=Yata(i)*sin(angle_at);
           else
               Yrer(i)=m*(1/rre(i)-1/Po)*((1/rre(i))^2)*(rat);% 分解的Fre1 向量
               Yata(i)=a*m*((1/rre(i)-1/Po)^2)*(rat^a);% 分解的Fre2 向量
               Yrerx(i)=Yrer(i)*cos(angle_re(i));%angle_re(i)=Y(i+1)
               Yrery(i)=-1*Yrer(i)*sin(angle_re(i));
               Yatax(i)=Yata(i)*cos(angle_at);%angle_at=Y(1)
               Yatay(i)=Yata(i)*sin(angle_at);
           end           
       else
            if X(2)>Xsum(i+1,2)
               Yrer(i)=m*(1/rre(i)-1/Po)*((1/rre(i))^2)*(rat);% 分解的Fre1 向量
               Yata(i)=a*m*((1/rre(i)-1/Po)^2)*(rat^a);% 分解的Fre2 向量
               Yrerx(i)=-Yrer(i)*cos(angle_re(i));%angle_re(i)=Y(i+1)
               Yrery(i)=1*Yrer(i)*sin(angle_re(i));
               Yatax(i)=Yata(i)*cos(angle_at);%angle_at=Y(1)
               Yatay(i)=Yata(i)*sin(angle_at);
            else
                Yrer(i)=m*(1/rre(i)-1/Po)*((1/rre(i))^2)*Rat;% 分解的Fre1 向量
                Yata(i)=a*m*((1/rre(i)-1/Po)^2)*rat;% 分解的Fre2 向量
                Yrerx(i)=Yrer(i)*cos(angle_re(i));%angle_re(i)=Y(i+1)
                Yrery(i)=Yrer(i)*sin(angle_re(i));
                Yatax(i)=Yata(i)*cos(angle_at);%angle_at=Y(1)
                Yatay(i)=Yata(i)*sin(angle_at);
            end
        end
      
        
    end%判断距离是否在障碍影响范围内
end
Yrerxx=sum(Yrerx);% 叠加斥力的分量
Yreryy=sum(Yrery);
Yataxx=sum(Yatax);
Yatayy=sum(Yatay);

三、运行结果

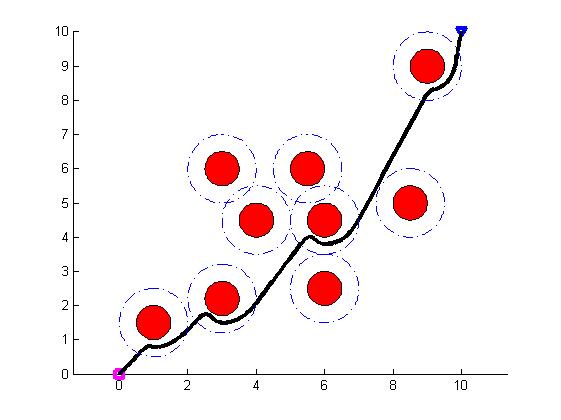
四、备注

版本：2014a

以上是关于人工势场法路径规划算法（APF）的主要内容，如果未能解决你的问题，请参考以下文章

路径规划基于matlab改进的人工势场算法机器人避障路径规划含Matlab源码 1151期

人工势场路径规划-matlab代码

路径规划基于人工势场的无人机三维路径规划matlab源码

无人机路径规划基于人工势场实现无人机编队路径规划matlab源码

二维平面内无人机的路径规划——势场法-改进

技术分享 | 基于人工势场法的无人机，机间避撞实现