1143. 最长公共子序列

Posted 2022-03-14 心脏dance

 题目链接：力扣

思路：动态规划入门题

先上递推式： dp[i][j] 表示 text1 前 i 个字符和 text2 的前 j 个字符的最长公共子序列 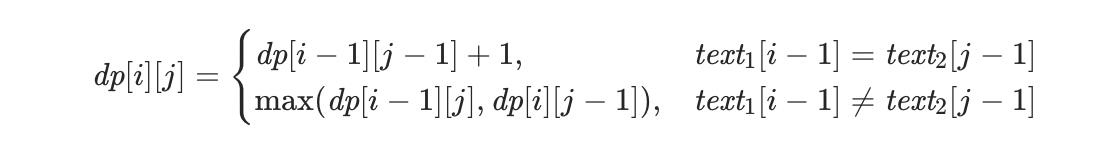 递推式怎么来的呢？

给定两个字符串 S1 ， S2，设序列 S1 = x1, x2, x3 ... xn , S2 = y1, y2, y3 ... ym , 的最长公共子序列是 S = z1, z2, z3 ... zk 。

1. 如果 xn = ym , 则 zk = xn = ym , 那么 S[k - 1] 就是 S1[n - 1] 和 S2[m - 1] 的 最长公共子序列

2. 如果 xn != ym , 且zk != xn , 那么 S[k] 就是 S1[n - 1] 和 S2[m] 的 最长公共子序列

3. 如果 xn != ym , 且 zk != ym , 那么 S[k] 就是 S1[n] 和 S2[m - 1] 的 最长公共子序列

所以我们很容易就得到递推式了

上代码（注意dp的初始化的值，都是0（不知道为啥的可以在下面评论哦～～～））：

import kotlin.math.max

class Solution 
    fun longestCommonSubsequence(text1: String, text2: String): Int 
        val dp = Array(text1.length + 1)  IntArray(text2.length + 1) 
        for (i in 1..text1.length) 
            for (j in 1..text2.length) 
                if (text1[i - 1] == text2[j - 1]) 
                    dp[i][j] = dp[i - 1][j - 1] + 1
                 else 
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
                
            
        
        return dp[text1.length][text2.length]