[硫化铂]题目名称
Posted StaroForgin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[硫化铂]题目名称相关的知识,希望对你有一定的参考价值。
题目名称
题目概述

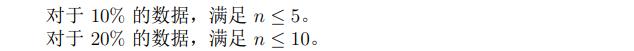
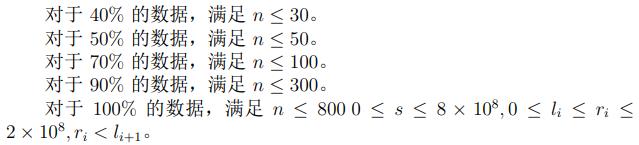
题解
看到这道题,我们显然不可能将每一个数都枚举一遍,也就是说,我们需要用更加简单的方式来表示我们这些数,生成函数正是一种很好的选择。
我们的生成函数
A
(
x
)
=
∑
i
=
1
n
∑
j
=
l
i
r
i
x
j
=
∑
i
=
1
n
x
l
−
x
r
+
1
1
−
x
A(x)=\\sum_i=1^n\\sum_j=l_i^r_ix^j=\\sum_i=1^n\\fracx^l-x^r+11-x
A(x)=∑i=1n∑j=lirixj=∑i=1n1−xxl−xr+1,如果我们是在四个集合中选显然直接乘起来就可以了,但我们是要求从一个集合中选出四个不重复的数集,也就是说,我们得在上面的基础上去重。
去重后有,
A
n
s
=
[
x
s
]
1
24
(
A
4
(
x
)
−
6
A
(
x
2
)
A
2
(
x
)
+
3
A
2
(
x
2
)
+
8
A
(
x
3
)
A
(
x
)
−
6
A
(
x
4
)
)
Ans=[x^s]\\frac124(A^4(x)-6A(x^2)A^2(x)+3A^2(x^2)+8A(x^3)A(x)-6A(x^4))
Ans=[xs]241(A4(x)−6A(x2)A2(x)+3A2(x2)+8A(x3)A(x)−6A(x4))该式本身,是在枚举我们相同数的可能,使得最后只有全部不同的数集可以留下。
具体的计算方式,可以看成一个解线性方程组的形式,计算比较简单。
好的,我们已经得到了我们的答案式子,考虑如何计算这
x
s
x^s
xs处的系数。
显然,对于后三个式子的贡献,我们完全可以暴力枚举贡献到
x
s
x^s
xs处的值是多少。
那原来的区间合并即可。
而对于前面两个式子,就有点复杂了。
A
4
(
x
)
=
1
(
1
−
x
)
4
(
∑
x
l
−
x
r
+
1
)
4
=
∑
i
=
0
s
(
s
−
i
+
3
3
)
[
x
i
]
(
∑
x
l
−
x
r
+
1
)
4
A^4(x)=\\frac1(1-x)^4(\\sum x^l-x^r+1)^4=\\sum_i=0^s\\binoms-i+33[x^i](\\sum x^l-x^r+1)^4
A4(x)=(1−x)41(∑xl−xr+1)4=i=0∑s(3s−i+3)[xi](∑xl−xr+1)4
显然,对于后面那个四次方式,我们可以看成两个二次方式子乘起来,不妨记乘完后有
m
m
m项有系数,第
i
i
i项次数为
a
i
a_i
ai,系数为
f
i
f_i
fi。
进而有,
A
4
(
x
)
=
∑
a
i
+
a
j
⩽
s
f
i
f
j
(
s
−
a
i
−
a
j
+
3
3
)
A^4(x)=\\sum_a_i+a_j\\leqslant sf_if_j\\binoms-a_i-a_j+33
A4(x)=ai+aj⩽s∑fifj(3s−ai−aj+3)
如果有组合数的话是相当不好维护的,考虑拆一下,可得
A
4
(
x
)
=
∑
a
i
+
a
j
⩽
s
f
i
f
j
(
s
−
a
i
−
s
j
+
3
)
(
s
−
a
i
−
a
j
+
2
)
(
s
−
a
i
−
s
j
+
1
)
6
=
∑
a
i
+
a
j
⩽
s
f
i
f
j
(
s
−
a
i
)
3
+
(
s
−
a
i
)
2
(
6
−
3
a
j
)
+
(
s
−
a
i
)
(
11
−
12
a
j
+
3
a
j
2
)
+
(
3
−
a
j
)
(
2
−
a
j
)
(
1
−
a
j
)
6
A^4(x)=\\sum_a_i+a_j\\leqslant sf_if_j\\frac(s-a_i-s_j+3)(s-a_i-a_j+2)(s-a_i-s_j+1)6\\\\ =\\sum_a_i+a_j\\leqslant sf_if_j\\frac(s-a_i)^3+(s-a_i)^2(6-3a_j)+(s-a_i)(11-12a_j+3a_j^2)+(3-a_j)(2-a_j)(1-a_j)6
A4(x)=ai+aj⩽s∑fifj6(s−ai−sj+3)(s−ai−aj+2)(s−ai−sj+1)=ai+aj⩽s∑fifj6(s−ai以上是关于[硫化铂]题目名称的主要内容,如果未能解决你的问题,请参考以下文章