# 技术栈知识点巩固——算法

Posted 2022-03-09 MarlonBrando1998

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了# 技术栈知识点巩固——算法相关的知识，希望对你有一定的参考价值。

技术栈知识点巩固——算法

哈希算法

哈希算法（Hash）又称摘要算法（Digest），哈希算法的目的就是为了验证原始数据是否被篡改，它的作用是：对任意一组输入数据进行计算，得到一个固定长度的输出摘要。

哈希算法最重要的特点就是：

相同的输入一定得到相同的输出；
不同的输入大概率得到不同的输出。

@Test
public void test5() 
    String strOne = "test1";
    String strTwo = "test2";
    logger.info("hash 值：", strOne.hashCode());
    logger.info("hash 值：", strTwo.hashCode());
    People peopleOne = new People(1,"张三",23);
    People peopleTwo = new People(1,"张三",23);
    logger.info("hash 值：", peopleOne.hashCode());
    logger.info("hash 值：", peopleTwo.hashCode());

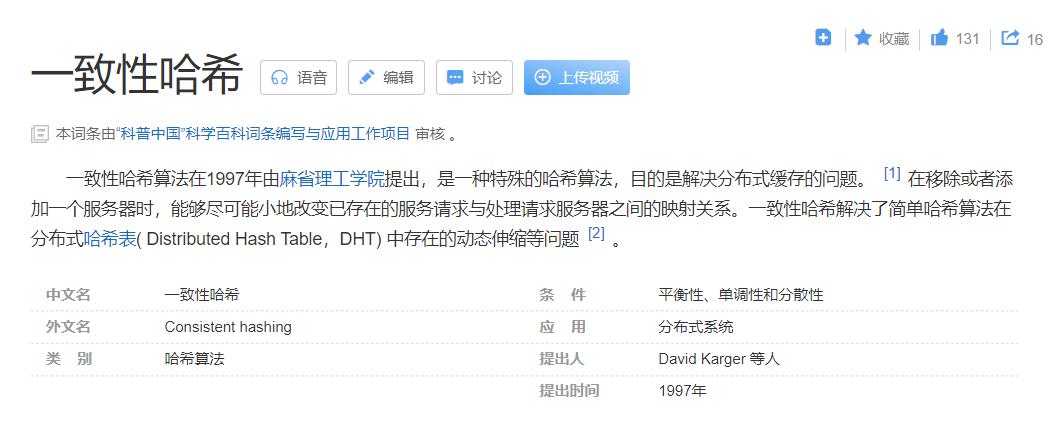
一致性哈希算法

二分查找

算法思路：左右指针移动，每次和中间的区间中间的数做比较，通过大小移动左右指针
实现方式：递归和while循环
注意点：start指针大于end指针退出循环体

public class TestDemo 

    private static final Logger logger = LoggerFactory.getLogger(TestDemo.class);

    /**
     * 二分查找
     */
    int[] arr = 10, 7, 4, 2, 6, 9, 8, 3, 22, 3, 44, 5;


    @Test
    public void test() 
        int num = 5;
        logger.info("数字: 在第： 位", num, sortFindNum(num, arr));
    

    private int sortFindNum(int num, int[] arr) 
        // 先对数组排序
        for (int j = 0; j < arr.length - 1; j++) 
            for (int k = 0; k < arr.length - 1; k++) 
                if (arr[k] > arr[k + 1]) 
                    int temp = arr[k];
                    arr[k] = arr[k + 1];
                    arr[k + 1] = temp;
                
            
        
        System.out.println("排序后的数组为：" + JSON.toJSONString(arr));
        // 对有序数组 二分查找
        int numOne = findNumOne(num, 0, arr.length - 1);
        return findNumTwo(num, 0, arr.length - 1);
    


    /**
     * 方法一 ： 缩小 start end 的值当 end-start==1的时候 num 和 arr[start] arr[end] 进行比较
     *
     * @param num
     * @param start
     * @param end
     * @return
     */
    private int findNumOne(int num, int start, int end) 
        while (start < end) 
            if (end - start == 1) 
                break;
            
            int flag = (start + end) / 2;
            int mid = arr[flag];
            logger.info("中间 mid:", flag);
            if (num == mid) 
                return flag;
             else if (num > mid) 
                start = flag;
             else 
                end = flag;
            
        
        return 0;
    

    /**
     * 递归方式
     *
     * @param num
     * @param start
     * @param end
     * @return
     */
    private int findNumTwo(int num, int start, int end) 
        if (start > end) return 0;
        int flag = (start + end) / 2;
        logger.info("===>" + flag);
        if (num == arr[flag]) 
            return flag;
         else if (num > arr[flag]) 
            start = flag;
         else if (num < arr[flag]) 
            end = flag;
        
        return findNumTwo(num, start, end);

滑动窗口算法

描述

滑动窗口算法在一个特定大小的字符串或数组上进行操作，而不在整个字符串和数组上操作，这样就降低了问题的复杂度，从而也达到降低了循环的嵌套深度。
滑动窗口主要应用在数组和字符串上。

实例

leetcode 3

给定一个字符串 s ，请你找出其中不含有重复字符的最长子串的长度。

字符串：abcdabcd

算法思路

列出满足题目的例子：括号中表示选中的字符以及最长的字符串

以(a)bcdabcd开始的最长字符串为(abcd)abcd
以a(b)cdabcd开始的最长字符串为a(bcda)bcd
以ab(c)dabcd开始的最长字符串为ab(cdab)cd
以abc(d)abcd开始的最长字符串为abc(dabc)d
以abcd(a)bcd开始的最长字符串为abcd(abcd)
以abcda(b)cd开始的最长字符串为abcda(bcd)
以abcdab(c)d开始的最长字符串为abcdab(cd)
以abcdabc(d)开始的最长字符串为abcdabc(d)

假设我们选择字符串中的第 k个字符作为起始位置，并且得到了不包含重复字符的最长子串的结束位置，为 r_k 。那么当我们选择第 k+1 个字符作为起始位置时，首先从 k+1 到 r_k的字符显然是不重复的，并且由于少了原本的第 k 个字符，我们可以尝试继续增大 r_k，直到右侧出现了重复字符为止。

解决思路

使用两个指针表示字符串中的某个子串（或窗口）的左右边界，其中左指针代表着上文中「枚举子串的起始位置」，而右指针即为上文中的 r_k；
在每一步的操作中，我们会将左指针向右移动一格，表示我们开始枚举下一个字符作为起始位置，然后我们可以不断地向右移动右指针，但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后，这个子串就对应着以左指针开始的，不包含重复字符的最长子串。我们记录下这个子串的长度；
在枚举结束后，我们找到的最长的子串的长度即为答案。

代码实现

@Test
public void testTwo() 
    String s = "pwwkew";
    Set<Character> set = new HashSet<>();
    int n = s.length();
    int end = -1;
    int index = 0;
    for (int i = 0; i < n; i++) 
        if (0 != i) 
            set.remove(s.charAt(i - 1));
        
        while (end + 1 < n) 
            boolean contains = set.contains(s.charAt(end + 1));
            if (contains) break;
            set.add(s.charAt(end + 1));
            end++;
        
        index = Math.max(index, end - i + 1);
    
    logger.info(String.valueOf(index));

递归算法

描述

实例

leetcode

面试题 08.05. 递归乘法

递归乘法。写一个递归函数，不使用 * 运算符，实现两个正整数的相乘。可以使用加号、减号、位移，但要吝啬一些。

算法实现

public int multiply(int A, int B) 
    if (A > B) 
        multiply(B, A);
    
    if (A == 1) 
        return B;
    
    if (A % 2 == 0) 
        return multiply(A >> 1, B) << 1;
     else 
        return (multiply(A >> 1, B) << 1) + B;

动态规划

描述

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

核心思想

拆分子问题，记住过往，减少重复计算。

实例

leetcode 509 斐波那契数

斐波那契数（通常用 F(n) 表示）形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。

解决思路

斐波那契数的边界条件是 F(0)=0F(0)=0 和 F(1)=1F(1)=1。当 n>1n>1 时，每一项的和都等于前两项的和，因此有如下递推关系：

F(n)=F(n-1)+F(n-2)
F(n)=F(n−1)+F(n−2)

由于斐波那契数存在递推关系，因此可以使用动态规划求解。

图形展示

算法实现

public int fib(int n) 
    if (n == 0) return 0;
    if (n == 1) return 1;
    int p, q = 0, r = 1;
    for (int i = 2; i <= n; i++) 
        p = q;
        q = r;
        r = p + q;
    
    return r;

队列

描述

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

实现队列

public class MyQueue 

    private List<Integer> list;

    /**
     * Initialize your data structure here.
     */
    public MyQueue() 
        this.list = new LinkedList<>();
    


    /**
     * Push element x to the back of queue.
     */
    public void push(int x) 
        list.add(x);
    

    /**
     * Removes the element from in front of queue and returns that element.
     */
    public int pop() 
        Integer integer = list.get(0);
        list.remove(0);
        return integer;
    

    /**
     * Get the front element.
     */
    public int peek() 
        return list.get(0);
    

    /**
     * Returns whether the queue is empty.
     */
    public boolean empty() 
        return list.isEmpty();

分治算法

描述

分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。即一种分目标完成程序算法，简单问题可用二分法完成。

实例

快速排序的实现

通过一趟排序将待排序列分割成两部分，其中一部分记录的关键字均比另一部分记录的关键字小。之后分别对这两部分记录继续进行排序，以达到整个序列有序的目的。

快排排序步骤

选择基准：在待排序列中，按照某种方式挑出一个元素，作为 “基准”
分割操作：以该基准在序列中的实际位置，把序列分成两个子序列。如果为升序，则此时，在基准左边的元素都比该基准小，在基准右边的元素都比基准大；而基准则在排序后正确的位置上。
递归地对两个序列进行快速排序，直到序列为空或者只有一个元素；

排序思路

以一个数组作为示例，取区间第一个数为基准数。

0	1	2	3	4	5	6	7	8	9
72	6	57	88	60	42	83	73	48	85

初始时，i = 0; j = 9; X = a[i] = 72

由于已经将 a[0] 中的数保存到 X 中，可以理解成在数组 a[0] 上挖了个坑，可以将其它数据填充到这来。

从j开始向前找一个比X小或等于X的数。当j=8，符合条件，将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++; 这样一个坑a[0]就被搞定了，但又形成了一个新坑a[8]，这怎么办了？简单，再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数，当i=3，符合条件，将a[3]挖出再填到上一个坑中a[8]=a[3]; j--;

数组变为：

0 1 2 3 4 5 6 7 8 9
48 6 57 88 60 42 83 73 88 85

0	1	2	3	4	5	6	7	8	9
48	6	57	88	60	42	83	73	88	85

i = 3; j = 7; X=72

再重复上面的步骤，先从后向前找，再从前向后找。

从j开始向前找，当j=5，符合条件，将a[5]挖出填到上一个坑中，a[3] = a[5]; i++;

从i开始向后找，当i=5时，由于i==j退出。

此时，i = j = 5，而a[5]刚好又是上次挖的坑，因此将X填入a[5]。

数组变为：

0	1	2	3	4	5	6	7	8	9
48	6	57	42	60	72	83	73	88	85

可以看出a[5]前面的数字都小于它，a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。

代码实现

public class QuickSort 

    private static final Logger logger = LoggerFactory.getLogger(QuickSort.class);

    @Test
    public void test() 
        int[] arr = 1, 5, 3, 4, 2, 6;
        quickSort(arr, 0, 5);
    

    private void quickSort(int[] arr, int begin, int end) 
        if (begin < end) 
            int i = begin;
            int j = end;
            // 基准元素
            int key = arr[begin];
            while (i < j) 
                // 从右向左找小于基准元素 z 的值填在 arr[i]
                while (i < j && arr[j] > key) 
                    j--;
                
                if (i < j) 
                    // 将 arr[j] 填到 arr[i] 上，arr[j] 就空了下来
                    arr[i] = arr[j];
                    // 从左向右找
                
                // 从左向右找大于或等于 x 的数来填 arr[j]
                while (i < j && arr[i] < key) 
                    i++;
                
                if (i < j) 
                    arr[j] = arr[i];
                    j--;
                

            
            //退出时，i等于j。将x填到这个坑中。
            arr[i] = key;
            quickSort(arr, begin, i - 1);
            quickSort(arr, i + 1, end);

贪心算法

描述

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。

实例

leetcode 455 分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

解决思路

首先对数组g和数组s排序，然后从小到大遍历 g 中的每个元素，对于每个元素找到能满足该元素的 s 中的最小的元素。具体而言，令 i 是 g 的下标，j 是 s 的下标，初始时 i 和 j 都为 0，进行如下操作。
对于每个元素 g[i]，找到未被使用的最小的 j 使得 g[i]≤s[j]，则s[j] 可以满足g[i]。由于g 和s 已经排好序，因此整个过程只需要对数组g 和 s 各遍历一次。当两个数组之一遍历结束时，说明所有的孩子都被分配到了饼干，或者所有的饼干都已经被分配或被尝试分配（可能有些饼干无法分配给任何孩子），此时被分配到饼干的孩子数量即为可以满足的最多数量。

算法实现

@Slf4j
public class Test455 

    @Test
    public void test() 
        int[] arr1 = 1, 2, 3, 4;
        int[] arr2 = 1, 3, 3, 4, 5, 6;

        int contentChildren = findContentChildren(arr1, arr2);
        log.info(String.valueOf(contentChildren));
    

    /**
     * @param g 每个孩子的需求量
     * @param s 饼干数
     * @return int
     */
    public int findContentChildren(int[] g, int[] s) 
        Arrays.sort(g);
        Arrays.sort(s);
        int m = g.length;
        int n = s.length;

        int count = 0;
        for (int i = 0, j = 0; i < m && j < n; i++, j++) 
            // 没有满足的情况
            while (j < n && g[i] > s[j]) 
                j++;
            
            if (j < n) 
                count++;
            
        
        return count;

… 未完待续

以上是关于# 技术栈知识点巩固——算法的主要内容，如果未能解决你的问题，请参考以下文章