nil Foundation的in-EVM Full Mina State Verification

Posted 2022-03-09 mutourend

1. 引言

nil Foundation系列博客有：

• nil Foundation的基于Solana light client实现的zk-bridge方案
• nil Foundation的Solana-Ethereum Bridge Based on Light-Client State Proof Verification

2021年2月，Mina Foundation和Ethereum Foundation发表联合request for proposals (RFP)，以在以太坊上支持recursive SNARK application。

该RFP会开放6周，欢迎在以太坊虚拟机上实现Pickles SNARK verification的设计和实现机制 proposals。以太坊基金会希望在以太坊上构建a verifier for Pickles SNARK，从而使得mina可be verified on Ethereum，从而可实现以太坊与mina之间的bridge。

经过严格筛选，nil Foundation赢得了120万美金的项目资金。

由于整个Mina Protocol state（archive nodes除外）都packed with the single Pickles SNARK proof （仅约22KB），因此，可将整个Mina Protocol state放入以太坊，从而可 以合理的gas cost在EVM中验证整个Mina Protocol state。

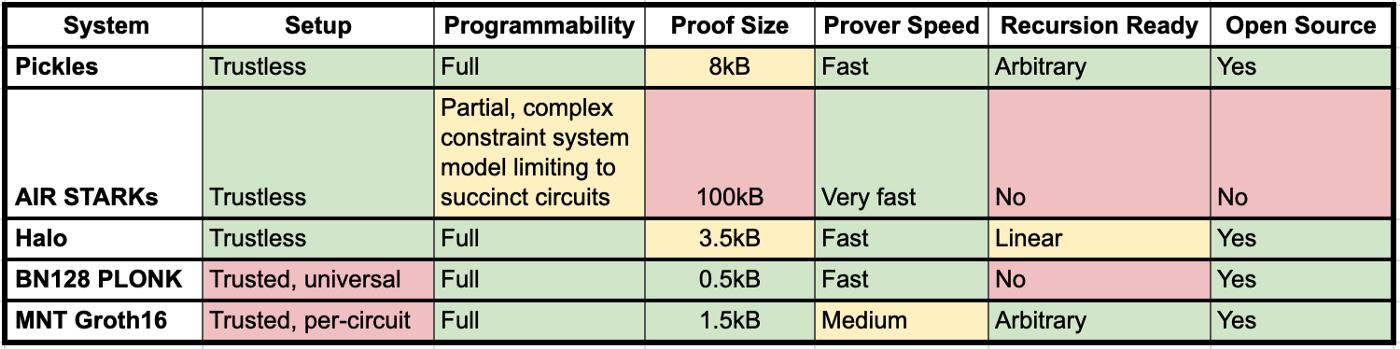
A full Mina Protocol state in-EVM verification意味着，可将所有发生在Mina链上的信息 带入到 以太坊链上，包括financial应用、provable computations等等。

2. 核心问题

核心问题在于：在EVM中直接验证Pickles SNARK非常昂贵。但是，可设计一种系统来对Pickles SNARK做某些预计算（如，计算a STARK that verifies the Pickles SNARK which itself may be efficiently verified on the EVM）。

Mina中的Pickles SNARK verifier的verification算法由以下元素组成：

• 1）根据the data of the proof，计算多个hash值。这包括了使用Poseidon hash函数 with 63 full rounds both over ${\mathbb{F}}_p$ and ${\mathbb{F}}_q$ with round constants，以及 基于${\mathbb{F}}_p$的MDS matrix 和 基于${\mathbb{F}}_q$的MDS Matrix。这一步非常便宜，可在EVM中以合理的gas实现。
• 2）检查多个arithmetic equations。这一步也很便宜，可在EVM中直接实现。
• 3）运行一个size 为$2n_2+4+(2+25)=63$的multi-scalar multiplication(MSM)运算，某些bases为fixed，某些bases为variable。这一步似乎可在EVM上以合理的效率实现，尽管要比第一步和第二步要贵。
• 4）对于每个$i$，运行a multi-scalar multiplication over $G_i$ of size $2^{n_i}$ with a fixed array of bases, and with scalars that can be very efficiently computed from the proof。

第4）步貌似无法直接在EVM中高效实现，除非可将计算切分为多块。

3. 引入Auxiliary STARK-based proof

Mina state verification的threshold cost为500万gas。因此，直接进行Pickles proof verification的gas不会超过500万。在Full verification of the Mina blockchain on EVM 中提出可向EVM额外提交一个STARK proof来证明a successful Pickles SNARK proof part verification，从而实现a valid in-EVM confirmation of everything what happened inside Mina。这种提交proof of successful proof verification的方法，似乎可控制在500万gas以内。

基于STARK的auxiliary proof的基本circuit中，包含的basic constraints（对应以上verification算法的第4）步）有：
令：

• 1）$P_1,P_2$为MSM results。
• 2）$n_1,n_2$为MSM sizes。
• 3）$G_1=[G_{1,0},\cdots ,G_{1,n_1-1}],G_2=[G_{2,0},\cdots ,G_{2,n_2-1}]$为the sets of fixed points。

则对于 $k=1,2$ 有：

• 1）$R_0=(0:1:0)$
• 2）$\forall 0\le i<n_k:R_{i+1}=R_i+f(s_i,G_{k,i+1})$，其中$f(s_i,G_{k,i+1})$的结果$s_{i+1}$是根据$s_i\ast G_{k,i+1}$计算而来的。
• 3）$R_{n_k-1}-P_k=(0:1:0)$

以上basic constraints可使用addition chains、Pippenger算法、STARK-friendly math等来优化，为Prover提供更好的性能，使Verifier需要更少的gas-cost。

额外还会研究，是将以上verification算法的第3）步包含在auxiliary proof中，还是直接在以太坊智能合约中进行验证。

不过，500万的gas确实太贵了。

4. 使gas更便宜

基于STARK的auxiliary proof verification所需gas仍然太昂贵，需要在auxiliary proof中寻找一种不同的SNARK方案。

R1CS（Rank-1 Constraint System-based） SNARK太昂贵了，已排除在外。

Spartan是transparent且有前途的，可在无需信任任何actor的情况下为以太坊生成所需提交的proof。如果需要信任a group of people来进行trusted setup，然后任何人都可基于trusted setup来生成Mina state proof？需要太多trust了。这也是为何SNARK transparency不是可选项，而是必选项。

基于PLONK proof scheme被认为是具有更便宜的verification cost。但是，大多数采用了Kate commitment scheme，需要trusted setup。

4.1 为何R1CS太贵？

需要a multiexp of size $2^{18}$ and one of size $2^{17}$ in a different curve。

R1CS system中最好的constraint cost per bit为：1 bit of scalar multiplication in 6 constraints，于是有：
$2^{18}$ scalar multiplications $\times$ (255 bits per scalar multiplication $\times$ (6 constraints/ 1bit)) = 401080320 constraints。

因此，若使用 sqrt(N)-cost DLOG-based polynomial commitment scheme，则Verifier需要do a multiexp of size $\sqrt{401080320}=20026$。

以上采用的是naive multiexp 算法。若使用Pippenger算法，约需要$2\times s\times n/{\log }_2(s\times n)$次group operation运算，其中$n$为multiexp size，在此处等于$20026$，$s$为scalar size，在此处为$255$。采用Jacobian坐标系，每次group operation约需要$16$次field multiplication，在EVM中，每次filed operation需要约8 gas。

因此，总的EVM cost约为：
$2\times 255\times 20026/{\log }_2(255\times 20026)\times 16\times 8=58,665,445$ gas

对于另一个size为$2^{17}$的multiexp，对应constraints数为14161，需要的EVM cost约为：
$2\times 255\times 14161/{\log }_2(255\times$