ML学习笔记 0 之综述
Posted 彭宇成
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ML学习笔记 0 之综述相关的知识,希望对你有一定的参考价值。
场景
这几个月断断续续学了一下吴恩达在coursera上发布的机器学习教程?国内的网络被墙了,看不了,花钱买了一个翻墙软件,终于可以看了,但网速太慢:学点东西真不容易。昨天晚上终于找到了一个地方,可以下载,可以下载,可以下载 - 开心!于是,果断又将第一周课程的第一部分看了好几篇。ok,从今天开始进入机器学习的学习与博客记录阶段:通过复述与简要概述作者的话,形成自己的机器学习体系 - 啊,进步的味道
笔记
一、引言
1.1 欢迎
机器学习无处不在。你我周围很多的应用程序或多或少的应用了机器学习的某个算法来使自己变得更加聪明,eg、百度搜索、今日头条的千人千面、电子邮件客户端:

如上图示,你把不感兴趣的邮件,比如广告邮件标识为垃圾邮件。 这样, Foxmail 后续收到类似(应该就是,邮件中出现某些关键词,比如说‘广告’等)的邮件,就直接放到‘垃圾邮件’这个分类里去了。下面通过一张图来对比人脑学习与机器学习过程:

1.2 监督学习-supervised learning
机器学习算法,根据是否需要提供正确的样本,可分为监督学习、无监督学习等。这里的监督就是指我们要告诉学习算法一些正确的样本数据,然后学习算法根据这些样本数据作出预测。举两个案例加以说明:
房价预测
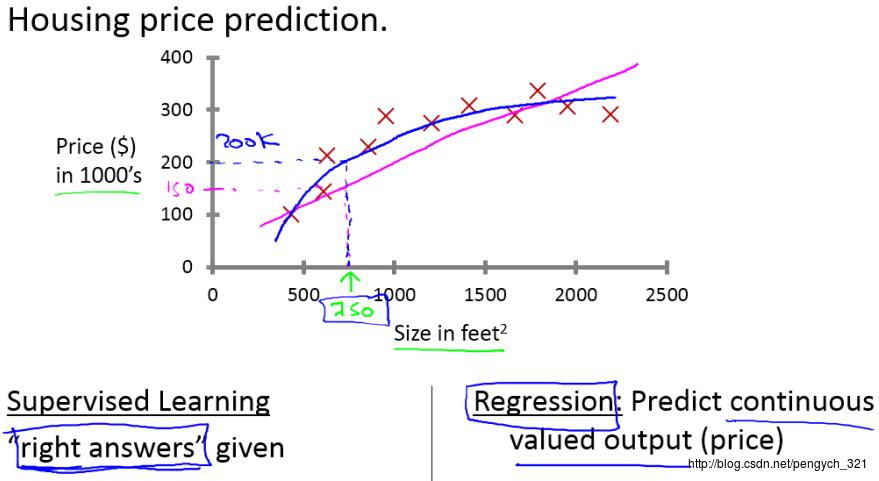
肿瘤良、恶性判断


由于问题1要预测未来三个月能卖出多少商品,由于卖出的商品数是连续的(虽然不是严格意义上的连续),故属于回归 问题;问题2预测的是0、1问题(hacked/compromised),故属于分类 问题
1.3 无监督学习-unsupervised learning
监督学习里的样本集有标签,比如肿瘤是良性还是恶性,而非监督学习集中的样本集没有任何标签,只是一堆数据。无监督学习就是从一堆没有标签的数据集中找出某种结构,并按照不同的结构分成不同的聚集簇。举两个例子:
1)谷歌新闻板块,每天从web上爬取大量的网页信息,然后按照不同的主题分类,组成有关联的新闻 - 这里谷歌的学习算法从大量的新闻数据集中,自动的按主题分类就一个无监督学习的业务场景。
2 ) 鸡尾酒宴问题
一首音乐作品中往往汇有多种乐器伴奏,比如汪峰的《像个孩子》中就有电吉他、钢琴、架子鼓等。怎么从这首歌曲中单独剥离出吉他与钢琴的声音?用无监督学习算法就可以做到:
[W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x');
基于matlab来搞的话,上面的一行代码就可以搞定。
这里,考虑到学习与工作效率,吴大师强烈建议同学们先用Octave或者Matlab建立原始模型,并测试通过以后,再用具体的编程语言去实现。
1.4 Other
增强学习与推荐系统
单变量线性回归-Linear Regression With One Variable
假设-Hypothesis
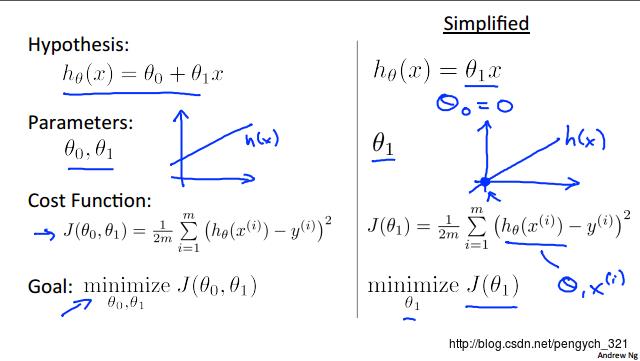
如图 1-2 所示,机器学习的关键在与找到一个合适的 模型 即 这里要写的 Hypothesis(简记为 h,如下图 2-1所示)。模型即数学里的公式,有线性的、非线性的。简单起见,这里假设房屋模型是简单的一元线性模型。




方式:固定θ1的值 => 求一元方程的最小值


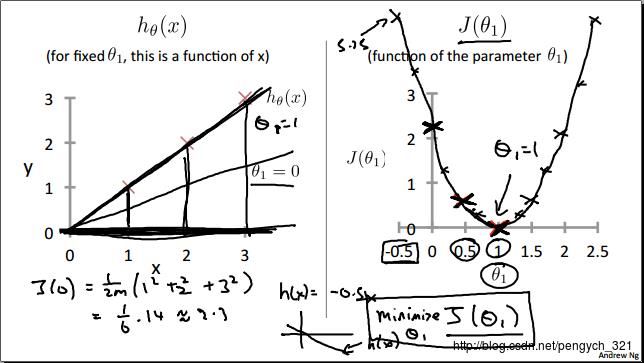


怎么求二元、三月、N元代价函数的最小值呢?这里先通过等高图来体验一下二元函数最小值求解过程,然后引出求解N元代价函数最小值的方法之一:梯度下降算法。

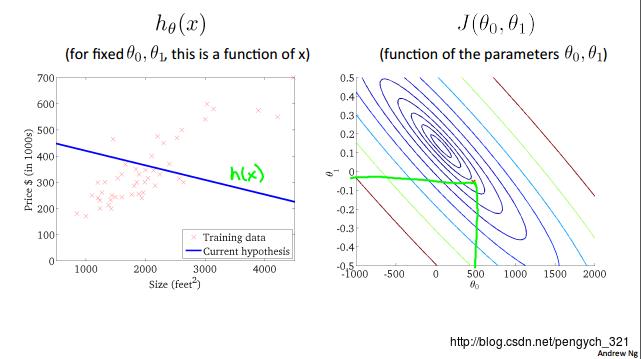

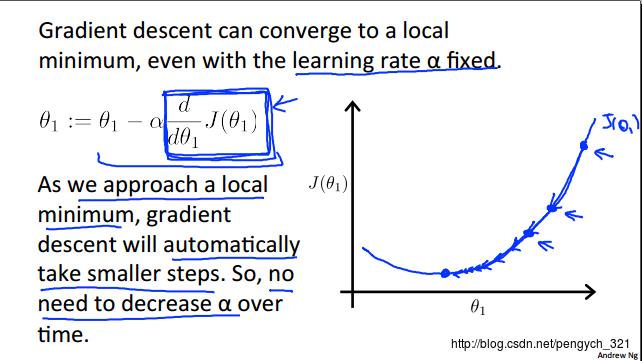
梯度下降算法 - Gradient descent

1)梯度下降算法,可用于求解N元函数 J 最小值时,变量 θ(i)的值
2)a 描述 J 移向最小值时的步伐:a 过小收敛速度越慢(即取得最小值所花的时间越长),a 过大可能取到的最小值偏差较大;实际项目中怎么选取 a 呢? 0.001 -> 0.01 -> 0.1 慢慢尝试;

参考
通俗理解卷积神经网络
看了上面这篇文章,写的很不错,就放到这里保存一下 - 内容跟本文描述无关
以上是关于ML学习笔记 0 之综述的主要内容,如果未能解决你的问题,请参考以下文章