信号与系统 2022 春季学期第二次作业

Posted 2022-03-05 卓晴

  ◎ 本文下载链接：

• 信号与系统分析2022 春季学期第二次作业 : https://zhuoqing.blog.csdn.net/article/details/123258268

  关于提交作业的基本要求，请参见： 通过提交两份作业综述对提交作业的基本要求 。

 

§01 基础作业

---

  基础作业部分包含有八道大题。请注意：

• 每道题目中包含有必做题与选做题两部分。
• 必做题要求包含在提交的作业中；选择题仅用于思考和练习。

1.1 信号奇偶分解

  绘制下图中各个信号的偶分量和奇分量。

1.1.1 必做题

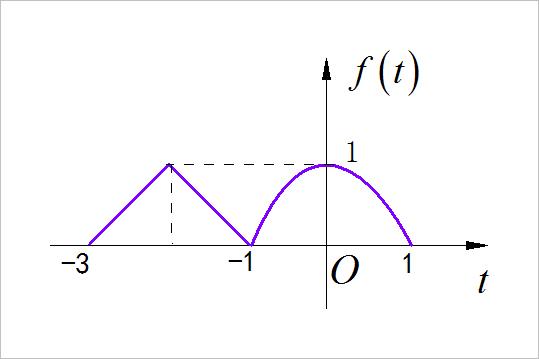
▲ 图1.1.1 第一小题

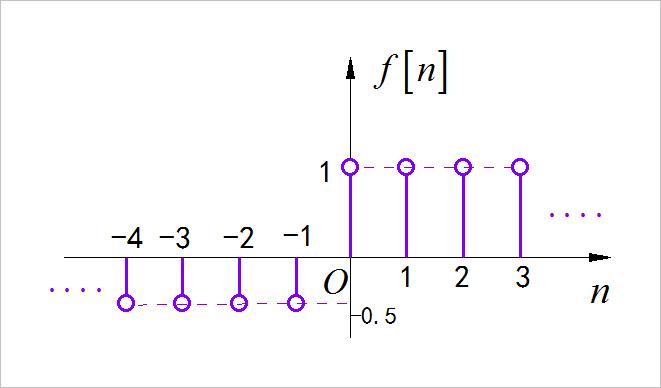
▲ 图1.1.2 第二小题

1.1.2 选做题

▲ 图1.1.3 第三小题

注意： 第三小题包括有两个冲激信号： $\delta \left(t-1\right),{\delta }^{\prime }\left(t\right)$ 。

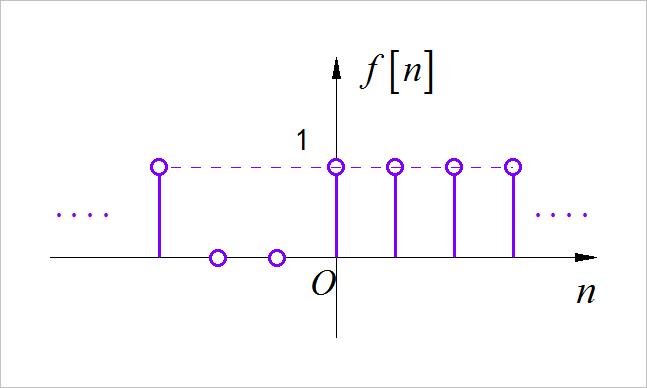
▲ 图1.1.4 第四小题

1.2 奇偶分解反问题

1.2.1 必做题

  已知下图中（a） $x_o\left(t\right)$ 是信号 $x\left(t\right)$ 的奇分量，图（b）是信号 $x\left(t+1\right)\cdot u\left(-t-1\right)$ 。绘制出 $x\left(t\right)$ 的偶分量 $x_e\left(t\right)$ 的波形。

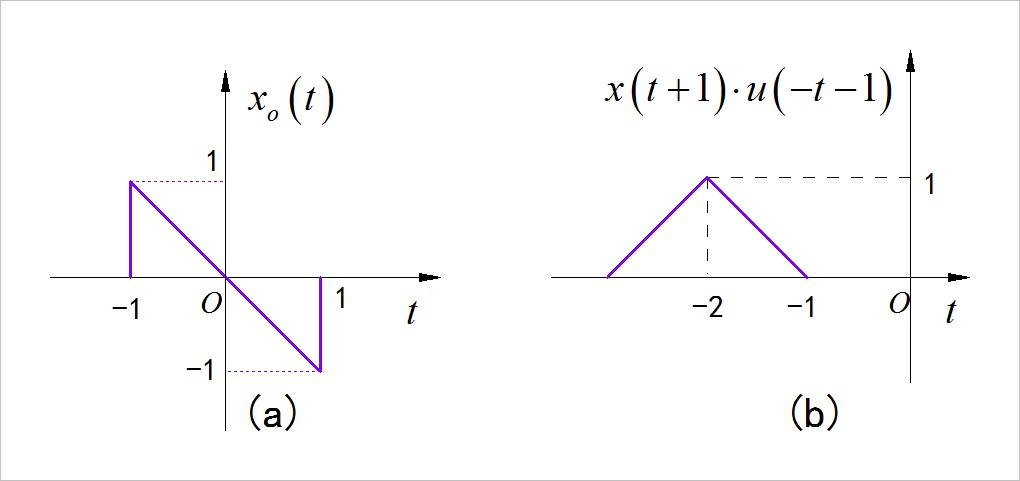
▲ 图1.2.1 本题中图（a）与图（b）信号波形

1.3 信号自变量变化

  已知连续时间信号 $f\left(t\right)$ 与离散时间序列 $f\left[n\right]$ 的波形如下，请绘制出对应自变量变化后的信号波形。

▲ 图1.3.1 本题对应的f(t),f[n]信号波形

1.3.1 必做题

1.3.2 选做题

1.4 从系统框图到方程

  试写出下面各图对应的系统输入输出之间的微分方程和差分方程。请大家注意本题中采用了不同的符号表示了积分、延迟，请大家注意辨识这些不同的表示方法。

1.4.1 必做题

▲ 图1.4.1 第一小题对应的连续时间系统框图

▲ 图1.4.2 第二小题对应的离散时间系统框图

▲ 图1.4.3 第三小题对应的系统框图

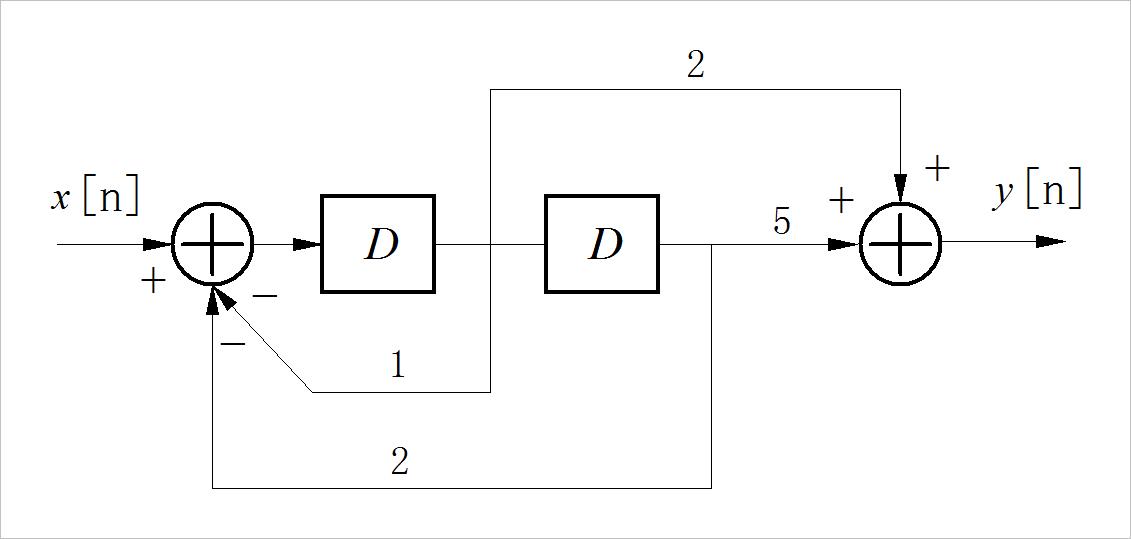
▲ 图1.4.4 第四小题对应的系统框图

注：本题中表示积分环节使用积分符号；单位延迟环节使用字母D表示。
提示：上面（3），（4）两小题，大家可以参考“算子方法”化简系统。具体参见课件【1,2,1,3】

1.4.2 选做题

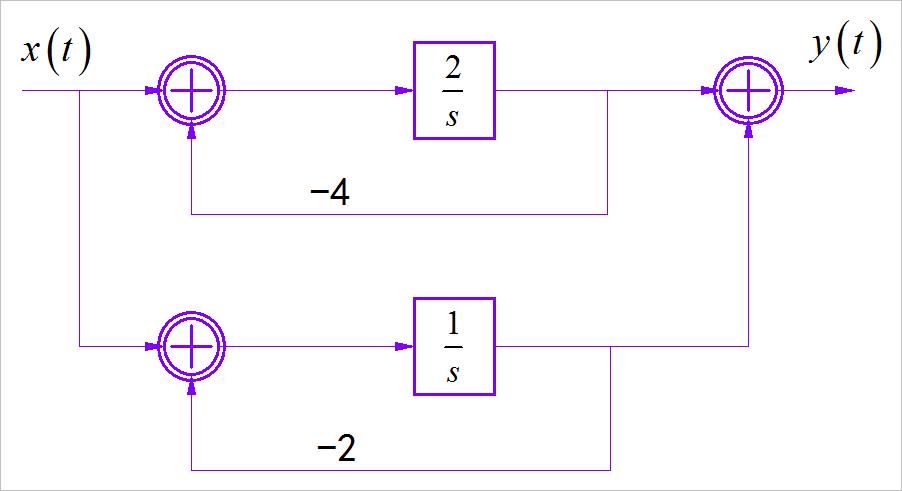
▲ 图1.4.5 第五小题系统框图

注：请注意在本题中对应的积分环节使用符合为 1/s 。
注：本题来自于 We have solutions for your book! 。

▲ 图1.4.6 第六小题系统框图

本题中的 a,b 都是常数。
本题来自于： Question: 4. [6 pts] System Equations From Block Diagram. Find the differe

▲ 图1.4.7 第七小题系统框图

注：本题中系统框图使用 $z^{-1}$ 单位延迟环节。
本题来自于： 第七小题系统框图

1.5 LTI系统响应

1.5.1 必做题

  有一线性时不变（LTI）系统，当激励 $e_1\left(t\right)=u\left(t\right)$ 时，系统响应 $r_1\left(t\right)=t\cdot e^{-2\alpha t}\cdot u\left(t\right)$ 。试求当激励 $e_2\left(t\right)=\delta \left(t\right)$ 时，系统响应 $r_2\left(t\right)$ 的表达式。

• 注：假定系统起始时刻系统初始条件为0，系统输入输出之间满足严格线性关系。

提示：本题需要应用到线性时不变系统的微分特性。

1.5.2 选做题

  Conside a LTI systems whose response to the signal $x_1\left(t\right)$ in Figure P5.1 is the signal $y_1\left(t\right)$ illustrated in Figure P5.2. Determine and sketch carefully the response of the system to the input $x_2\left(t\right)$ and $x_3\left(t\right)$ illustrated in the Figure P5.3 and P5.4 respectively.

▲ 图1.5.1 LTI系统的输入输出信号

提示：利用线性时不变系统的特性。将 $x_2\left(t\right),x_3\left(t\right)$ 分别表示成 $x_1\left(t\right)$ 与其延迟信号的线性组合，然后再根据LTI的性质，获得 $x_2\left(t\right),x_3\left(t\right)$ 各自的输出信号。

1.6 系统可逆性

  判断下列系统是否可逆。如果可逆，给出它的逆系统。如果不可逆，指出是该系统产生相同输出的两个输入信号。

  题目中，系统输入信号为 $e\left(t\right)$ 、 $e\left[n\right]$ ，输出信号为 $r(t以上是关于信号与系统\; 2022\; 春季学期第二次作业的主要内容，如果未能解决你的问题，请参考以下文章$

2021年春季学期-信号与系统-第十二次作业参考答案

信号与系统分析2022春季作业-参考答案：第二次作业

信号与系统 2023（春季） 作业参考答案 - 第二次作业

2021年春季学期-信号与系统-第十二次作业参考答案-第六小题

信号与系统 2022 春季学期第一次作业

信号与系统2022春季学期：作业内容与参考答案