轨迹优化问题

Posted 2022-03-03 Leokadia Rothschild

该文用于轨迹优化技术的transcription方法。前几节描述了用于将轨迹优化问题转化为一般约束优化形式的两类transcription方法(shooting methods and simultaneous methods.)。中间部分讨论了对基本方法的一些扩展，包括如何处理混合系统(如行走机器人)。最后一节介绍了各种实现细节。

1 Optimal Control Overview

求解最优控制问题[4]的算法有三种:

• 动态规划:在整个状态空间上求解Hamilton-Jacobi-Bellman方程。
• 间接方法:Transcribe problem，然后找到目标的斜率为零的地方。
• 直接方法:Transcribe problem，然后找到目标函数的最小值。
  动态规划是无约束低维系统最优控制问题的一个很好的解决方案，但它不能很好地适用于高维系统，因为它需要全状态空间的离散化。间接方法在数值上往往不稳定，并且难以实现和初始化[2]。在本文的其余部分，我们将把重点限制在记录和解决最优控制问题的直接方法上。通过转录解决最优控制问题的方法可以很好地适用于高维系统，但通过状态和控制空间产生的是单一的轨迹，而不是像动态规划那样的全局策略。

1.1 轨迹优化问题

轨迹优化问题寻求的是在满足约束条件的同时最小化代价函数的动态系统的轨迹。下面，我给出了一个轨迹优化问题的总体框架。

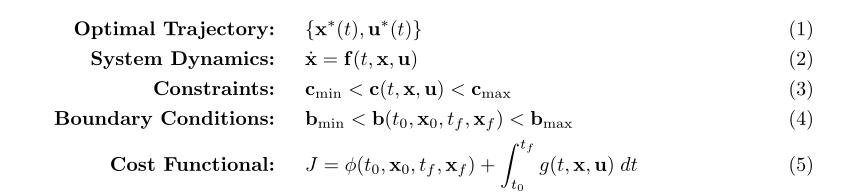
要指出的一件有趣的事情是状态x和控制u之间的区别。状态变量是在动力学方程中被微分的变量，而控制变量只在动力学方程[2]中以代数形式出现。在某些情况下，还可能存在未知参数(没有显示)，这些参数是在动力学方程中以代数形式出现的时不变变量。

1.2 Non-linear Programming

求解最优控制问题的Transcription方法通过将一个连续问题(第1.1节)转换为非线性规划问题(7)来工作。一旦采用这种形式，问题就可以传递给一个商业求解器，如SNOPT[6]、IPOPT[13]或FMINCON[8]。

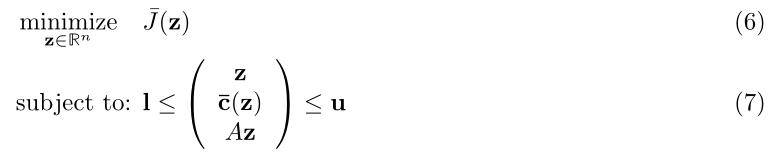
有很多Transcription算法可以实现这种转换，但它们都可以分为两大类:shooting methods 和simultaneous methods.。不同之处在于每种方法如何对系统的动态施加约束。射击方法使用模拟来明确地执行系统动态。同时方法在沿着轨迹的一系列点上加强动力学。

2 Shooting Methods

Single-shooting可能是transcribing最优控制问题的最简单方法。考虑一下用大炮击中目标的问题。你有两个决策变量(射击角度和火药质量)和一个约束条件(弹道穿过目标)。动力学很简单(抛射运动)，代价函数是火药的质量。单次拍摄的方法类似于一个人通过实验所能达到的效果。你猜测一下火药的角度和数量，然后发射大炮。如果你射过了目标，那么也许你会在下次测试中减少火药的质量。通过重复这种方法，你最终将能够击中目标，同时使用尽可能少的粉末。单次射击也是如此，只是用模拟代替了实验。

在更一般的单次射击的情况下，有一个连续的控制输入，你可以选择一个任意的函数来近似输入。一些常见的选择是零阶保持，分段线性，分段三次，或正交多项式。如果控制是用分段函数建模的，那么您必须注意将控制的不连续点与仿真中的积分步骤对齐。

单次拍摄对于简单的问题来说已经足够好了，但是对于更复杂的问题来说，它几乎肯定会失败。这是因为决策变量与目标和约束函数之间的关系不能很好地通过非线性规划求解器使用的线性(或二次)模型来逼近。

多重射击的原理是将一条轨迹分解成若干段，然后使用单次射击对每个段进行求解。随着线段的缩短，决策变量与目标函数和约束之间的关系变得更加线性。在多次拍摄中，一个片段的结束不一定与下一个片段的开始相匹配。这种差异被称为缺陷，它被添加到约束向量中。添加所有的片段将增加决策变量的数量(每个片段的开始)和约束的数量(缺陷)。尽管这看起来可能会使低级优化问题变得更加困难，但实际上却使它变得更加容易。

图1为单拍与多拍对比图。

3 Simultaneous Methods

Simultaneous Methods有很多种。Simultaneous Methods与ShootingMethods的关键区别在于，同时方法直接用决策变量表示状态轨迹，然后仅满足轨迹中特殊点的动力学约束。

3.1 Integral vs Differential Form

对于任何一个轨迹优化问题，动力学约束都有两种不同的写法:导数和积分。导数法规定状态对时间的导数必须等于˙x = f (x, u))。积分法规定状态轨迹必须符合动力学对时间的积分(x = R f (x, u) dt)。注意，shooting
methods是积分法的一种。

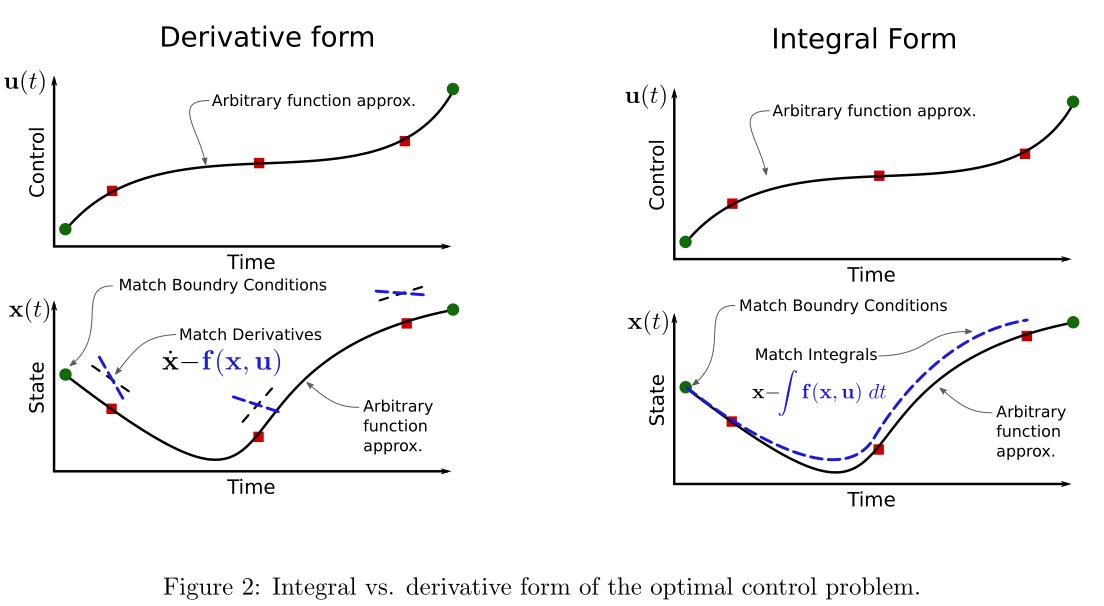
图2显示了这一差异的漫画

3.2 Orthogonal Collocation

Orthogonal Collocation是一种利用正交多项式逼近状态和控制函数的同时(配置)方法。正交多项式有几个有用的性质。它的关键概念是一个多项式可以用它在某个有限域上的一个特殊网格点集合上的值来表示。当用这种形式表示时，很容易对多项式[1]进行快速、准确的数值插值、微分和积分。

3.3 H vs P scheme

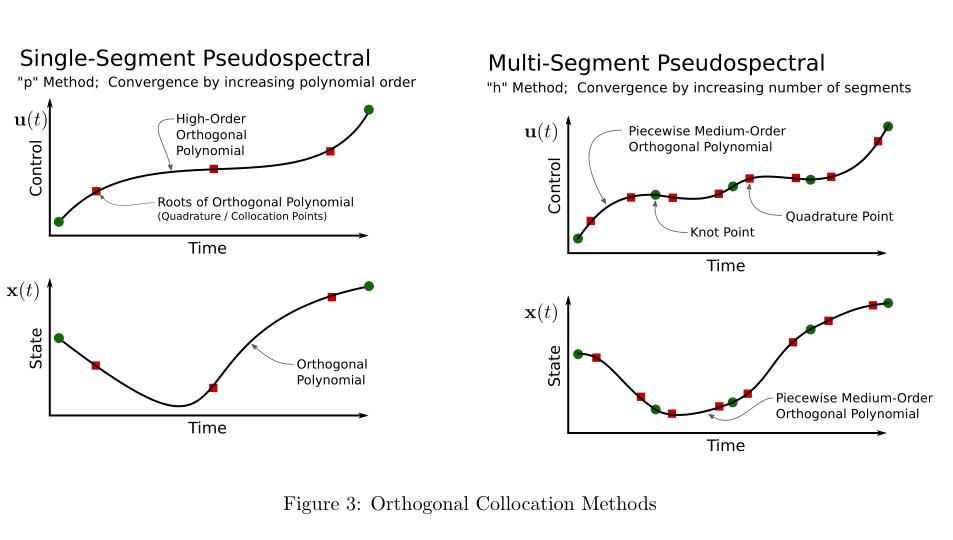
最简单的正交配置形式是将整个轨迹表示为一个单高阶正交多项式。对动力学的约束(无论是积分形式还是导数形式)应用于配置点，这些配置点被选择在正交多项式的根处。然后通过轨迹上的数值求积来计算代价函数，它只是每个配置点上函数值的加权组合。该方法通过增加多项式的阶数(p-方法)来获得收敛性。

如果底层的解是解析的，那么将整个轨迹表示为一个单正交多项式就很好。在许多情况下，这是不正确的，例如当执行器饱和时。在这些情况下，多项式近似在不连续点附近必然失效。一种解决方法是将轨迹表示为一系列中等阶正交多项式。轨迹的每个部分都与缺陷约束缝合在一起，就像在多次射击中一样，并且在给定的段内的动力学是使用配置点的约束来表示的。两个线段相连的点称为结点。这种方法的收敛性是通过增加轨迹段数(h法)来实现的。图3显示了单段和多段正交配置方法的比较。

最复杂的方法在此基础上更进一步，自适应地细化轨迹上的结点数目和位置，以及每个线段[10]上的多项式的阶次。这是商业上可用的转录算法GPOPS[11]所采用的方法。

3.4 Special Cases

常用的同时进行的方法有直接转录法和直接搭配法。直接转录是一种采用动力学约束的积分形式的同步方法。控制被表示为一个分段常数轨迹，并且状态是分段线性的。优化中的决策变量是每个结点的控制值和状态值。直接搭配类似于直接转录，但输入表示为时间的分段线性函数，状态为分段立方。每个结点的状态值和控制值是决策变量。状态斜率由每个结点的动力学特性来确定。配置点是每个立方体线段的中点。配置点处的三次体的斜率被约束以匹配该点处的系统动力学。图4。

4 Dealing with Hybrid Systems

混合系统是一个动态系统，它具有多个连续动态阶段，由离散过渡分开。混合系统最简单的例子是一个弹跳球。它有一个单一的连续运动阶段(自由落体)和一个单一的离散过渡(与地面碰撞)。

更复杂的混合系统是一个步行机器人。连续模式的几个例子可能是:

•飞行-双脚都在空中
•双站-双脚都在地上
•单站-双脚都在地上

然后在这些模式之间会有一个离散的过渡。有些过渡不会改变连续状态(例如将一英尺抬离地面)，而其他过渡会改变连续状态(脚与地面碰撞)。

处理这种混合系统的一种简单方法便是将它们捆绑在一个大型模拟或动态函数中，并尝试着创造一种简单的转录方法。这几乎肯定会失败。原因是，底层的优化算法通常是一个平滑的，基于梯度的方法(例如。SNOPT、IPOPT FMINCON)。混合系统的离散过渡导致系统的动力学是非光滑的。例如，一个变量中的一个小变化可能导致碰撞发生在不同的时间，这将导致缺陷约束中的一个巨大的变化。

处理混合系统有两种普遍接受的方法:多相法和贯穿接触法。多阶段方法更快、更准确，但它们需要明确地了解转换的顺序。通过接触方法可以处理任意的接触序列，但速度较慢，精确度较低。

这两种方法类似于模拟混合系统的两种不同方法。多相转录类似于利用事件检测模拟有限状态机。通过接触类似于时间步进。

4.1 Multi-Phase Methods

Multi-Phase Methods是对基本的多次拍摄或配置算法的一种较为简单的扩展。首先，用户决定应该出现哪个阶段序列。例如，在行走机器人中，这可能是单站姿(一只脚在地上)，然后是双站姿(两只脚在地上)。然后，在每个连续阶段中建立的约束与在一个更简单的问题中完全相同。然后加入一组约束条件，使连续相切换到一起，满足过渡方程。这种方法的一个有趣的副作用是，在运动的每个阶段，系统的状态可能完全不同，只要有某种合理的方式将它们连接起来。这很有用，因为这意味着每组连续动态都可以用最小坐标表示。商用转录程序GPOPS II[11]为使用多阶段方法建立和求解混合系统轨迹提供了一个复杂的接口。

4.2 Through-Contact Methods

Through-Contact Methods是一种完全不同的方法。它们直接处理每个网格点的接触约束，而不是将动力学中的不连续点推到每个阶段之间的特殊约束中。通过接触优化的关键思想是，如果它们是由约束直接处理的，不连续是细化的。这是通过将系统动力学写成基于脉冲的形式来实现的，并且任意地保留接触脉冲(而不是通过假设接触模式来代数地消除它们)。然后将(未知的)接触脉冲作为控制变量，在每个网格点受以下约束:

这些约束条件将为每个网格点上的接触脉冲提供一个唯一的解。这对于复杂的行为特别有用，如双足爬行或从躺着的位置站起来，如Mordatch等人[9]所示。

Through-contact trajectory optimization 很快将作为德雷克[12]的一部分，这是一个用于机器人控制设计和分析的工具箱。

Through-contact trajectory optimization

如果接触模式的顺序未知，则通过接触法可能更精确，因为它可以找到多相法中规定的相位顺序所排除的解。也就是说，如果两种方法都能找到大致相同的解，那么多相方法将会更加精确。

多相方法可以非常精确，因为优化是隐式地求每个连续运动阶段之间的过渡的根。此外，连续的轨迹可以很容易地用高阶多项式表示(可以直接搭配，也可以通过多次拍摄的龙格-库塔格式间接表示)。这些高阶轨迹能够很好地匹配真解，即使是相对较大的时间步长，因为误差与多项式的阶数成正比。

由于连续运动阶段之间的过渡被约束在网格点上，无法独立调整，因此通过接触的方法在其精度方面存在固有的局限性。这意味着近似误差与步长成正比，极大地限制了获得高精度解的能力。

5 Setting up your problem

5.1 Grid Selection

射击法和同时法都有一些自由参数来控制用来记录问题的网格。一般来说，您需要精细的网格来获得准确的解决方案，但如果最初的猜测不是很好，这可能会导致收敛问题。一个常见的解决方案是使用一个非常粗的网格来找到一个近似的解，然后使用这个近似解作为第二次或第三次使用更细网格的优化的初始猜测。商用程序GPOPS II使用复杂的算法[3]自动处理这种网格优化。

5.2 Initialization

即使是一个很好的轨迹优化也可能因为一个糟糕的初始化而失败。初始化轨迹的一个好方法是猜测轨迹上的几个点，然后对这些点拟合一个多项式。然后这个多项式可以被微分一次得到状态的一阶导数，再次得到联合加速度。逆动力学可以用来计算产生这些加速度所需的关节力矩。然后插值这个粗略的猜测，以得到正确的网格点，无论是你的多次拍摄或搭配方法。初始化过程中可能出错的一件事是，您从一个不可行的、但局部最优的解决方案开始优化。当您将初始控制功能设置为零时，通常会发生这种情况。这可以通过添加一个小的随机噪声沿初始猜测执行器修正。这有一个额外的好处，就是在每次迭代中从一个新的位置开始优化，这有时有助于检测局部最小值。有时，即使初始化合理，如果代价函数过于复杂，优化也会失败。一种解决方案是编写优化使用替代成本函数，如力矩的平方，这是很简单的优化。如力矩的平方，这是很简单的优化。

5.3 Local Minimum

一旦你有了轨迹优化问题的“收敛”解决方案，这是一个很好的实践，检查解决方案是否是“真实的”(全局)解决方案。在大多数情况下，没有实用的方法来证明您已经找到了全局解，但您可以从几个初始猜测运行优化，并检查它们都收敛到相同的解。图5显示了一个带有三个次最优局部最小值和一个全局最小值的一维约束优化问题的画面。

Smoothness and Consistency

为了使一个轨迹优化程序收敛，所有的内部函数调用必须是平滑的和一致的:

•平滑-函数的输出是连续的，并且在所有点上至少有两次可微。理想情况下，所有衍生品都应该保持小尺寸——尖锐的(连续的)棱角仍然会造成问题

•一致-函数的输出是可重复和平滑的多个调用;计算机在每次调用(no if语句)时执行完全相同的代码行。

这两个要求听起来很简单，但实际上却非常难以处理。在本节中，我将尝试介绍几个常见的出错点。注意，这些需求同时适用于约束和目标函数。

6.1 Dynamics

行走机器人是混合系统——它们的动态既有连续的方面，也有离散的方面。如第4节所讨论的，这些离散动力学必须通过使用贯穿接触或多阶段转录方法小心处理。另一个常见的误差来源是在对多种射击方法的动力学函数的模拟中。在拍摄方法中，重要的是使用明确的、固定步长的积分算法，而不是像ode45这样的自适应方法。

有时候，我们很容易在动态中加入一些噪音。这就保证了函数是不一致的，并且几乎肯定会导致优化程序失败。一般来说，在轨迹优化程序中调用随机数生成器并没有很好的理由。

6.2 Objective Function

在一个目标函数中有许多不连续的来源，通常是由于看起来无关紧要的函数。一些例子是取一组数字的最大值或最小值，绝对值函数，钳位函数和斜坡函数。处理这些不连续函数的最佳方法是使用一个约束来实现不连续。这是因为非线性程序求解器内置了处理约束条件的特殊工具。公式8显示了处理函数|x|的正确方法。其他示例在[7]中提供

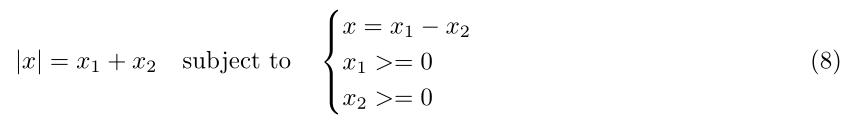
处理不连续函数的另一种方法是使用“平滑”近似，如下图所示:

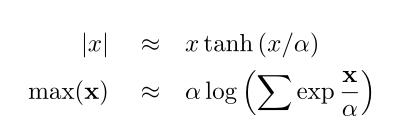
这种方法是有效的，但它通常比约束方法更不精确，需要更长的时间来收敛。即使平滑的函数是连续的，在精度和收敛之间有一个折衷。如果平滑度较大，则优化程序会收敛，但解不准确。如果平滑度很小，程序将缓慢收敛，或者根本不收敛。一种解决方案是迭代地减少平滑，从大量的平滑开始以获得一个可行的解决方案，然后减少平滑到答案的零。

有两种方法可以平滑地逼近函数。第一种方法是使用指数函数，使其渐近接近离不连续点远的真函数。第二种方法是使用函数的分段版本，在这里，不连续点附近的区域用多项式近似代替。

7 Software Specifics

一旦轨迹优化问题被多次射击或配置记录下来，就必须用非线性约束优化求解器来求解。最流行的两个算法是SNOPT和FMINCON。下面的部分描述了一些在使用这些程序时很有帮助的具体细节。FMINCON似乎是通过先找到一个可行的解决方案，然后尝试对其进行优化来解决多重射击问题的。

这意味着FMINCON可以处理比SNOPT更糟糕的初始猜测，但在寻找真正的最优解决方案方面，它略逊一筹，因为它在约束条件中没有太多灵活性。

你可以买一个商业版本的转录算法，而不是自己写。现在可用的最好的软件可能是GPOPS II，它内部调用SNOPT或IPOPT(另一种求解器，这里没有讨论)。

7.1 SNOPT [6]

一个单一的函数调用用于目标函数和所有约束。这个函数返回一个向量，向量的第一个元素是目标函数的值。以下所有元素都是约束。SNOPT不要求用户指定哪些约束是线性的或非线性的——它会自动计算。因为SNOPT结合了目标函数和约束函数，所以您总是需要为目标函数提供一个值，即使您只是在解决一个可行性问题。在这种情况下，目标函数的值应该设为零。更重要的是，您还必须指定目标函数的边界也是零。在代码中，这看起来像:F(1)==0, Flow(1)==0, Fupp(1)==0不要在你的目标函数或约束中使用常数项。所有常数项必须移动到边界向量(Flow, Fupp)。这是因为SNOPT内部存储和估计梯度的方式——它将在数值上删除任何常数项。SNOPT不允许用户向目标函数传递任何参数，至少在从Matlab调用时是这样。解决这个问题的一种方法是创建一个参数结构，并将其保存为一个全局变量。完成此操作后，您就可以从全局变量中读取参数。

7.2 FMINCON [8]

FMINCON要求目标函数和约束函数在不同的函数中。这就产生了一个问题，因为约束和客观都需要评估每个网格点的动态。为了避免重复做所有的工作，最好使用一个持久变量(在c++中这是一个静态变量)。创建一个完成动态集成的单一函数，并让它存储最后的输入状态和输出解决方案。当调用它时，它检查状态是否与上次相同—如果是，则返回之前的解决方案。在FMINCON中有一个各种各样的bug，它阻止你使用状态边界来限制一个特定的值。基本上，说:0 < x <= 0会导致FMINCON在进行有限差分时尝试除以机器精度的步长。最好把这些东西作为等式约束，这是一种特殊的处理方式。

7.3 GPOPS2 [11]

GPOPS2是一款商用软件，实现了“用变阶自适应正交配置方法和稀疏非线性规划解决最优控制问题的通用软件”。该程序擅长于解决已知接触模式序列的轨迹优化问题，这是一个非常一般的解算器。根据我的经验，它通常比使用更简单的多重拍摄或搭配方法更快、更准确。

8 Miscellaneous

本节讨论了一些奇怪的主题，这些主题对于理解它们很有用，但不适合放在其他地方。

8.1 Regularization

可以创建一个没有唯一解的最优轨迹问题。这通常会导致收敛问题，因为优化程序在看似相等的解之间来回跳跃。这个问题是通过添加一个小的正则化项到目标函数，这迫使一个唯一的解决方案。对于动力系统，我发现在代价函数中加入一个小的输入平方项通常是充分的。我发现正则化项比主要目标项小6-8个数量级，通常仍然有效。

8.2 Constraint on Controls

将非线性约束应用于轨迹边界的控制的正确方法是创建一个虚拟状态来表示控制，然后让优化程序确定控制的导数。然后利用系统动力学来确保控制及其导数的可行性。这项技术对于强制行走机器人的接触力保持在其摩擦锥内特别有用

8.3 Optimizing a Parameter

假设你想找到一个最优的轨迹，但是至少有一个自由参数用于你的设计。在传递给底层优化函数时，很容易将这个参数作为附加项添加进去。这不是一个好主意，因为它结合了约束的雅可比矩阵，这几乎和用单次射击来解决问题一样糟糕。正确的做法是向系统添加一个控件，并使用控件而不是参数。然后添加一个特殊的约束，以确保控制在整个轨迹中保持恒定。这将快速解决可能的最佳参数选择，同时保持约束和目标函数的雅可比矩阵的稀疏。

9 Hammer Example

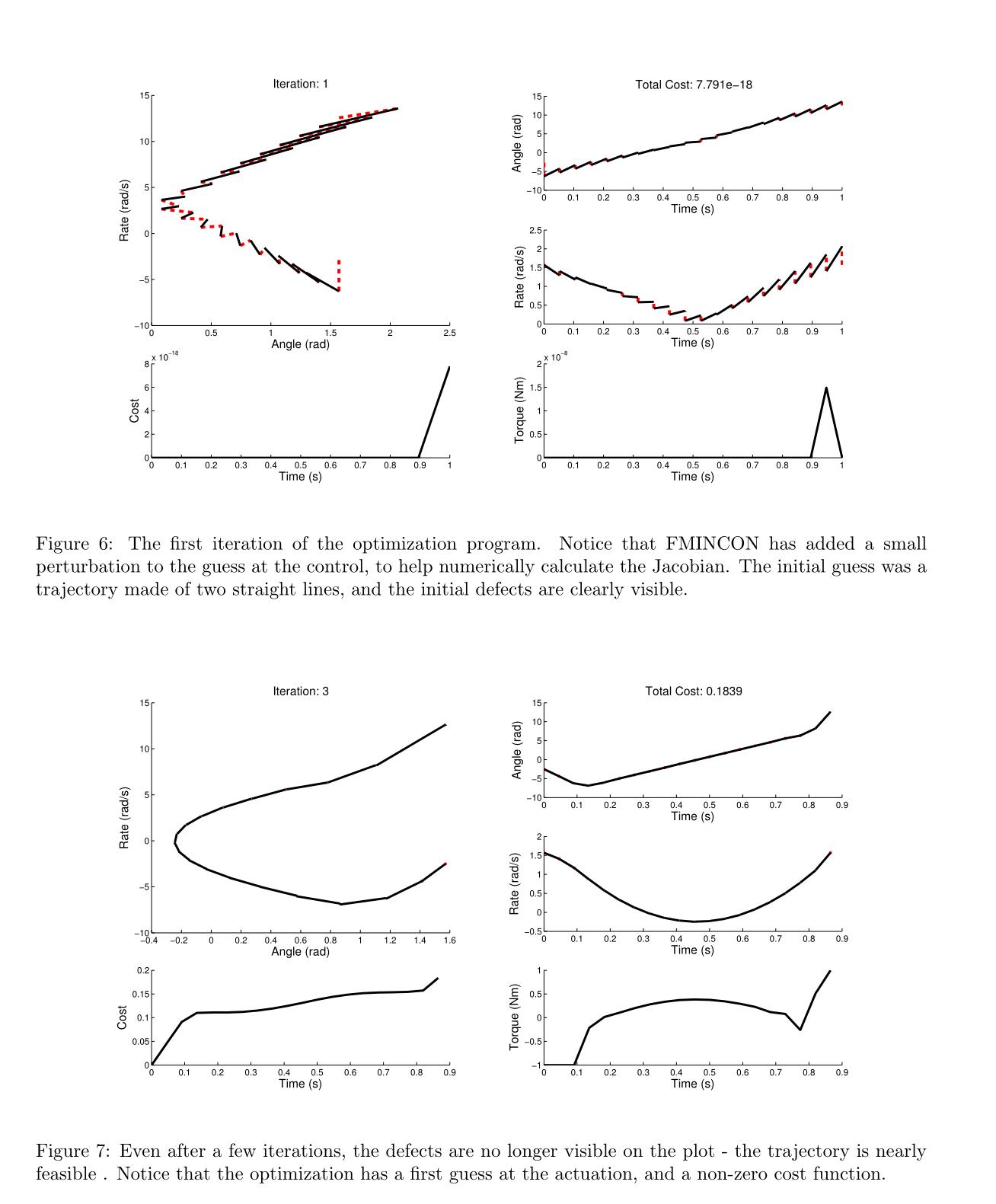
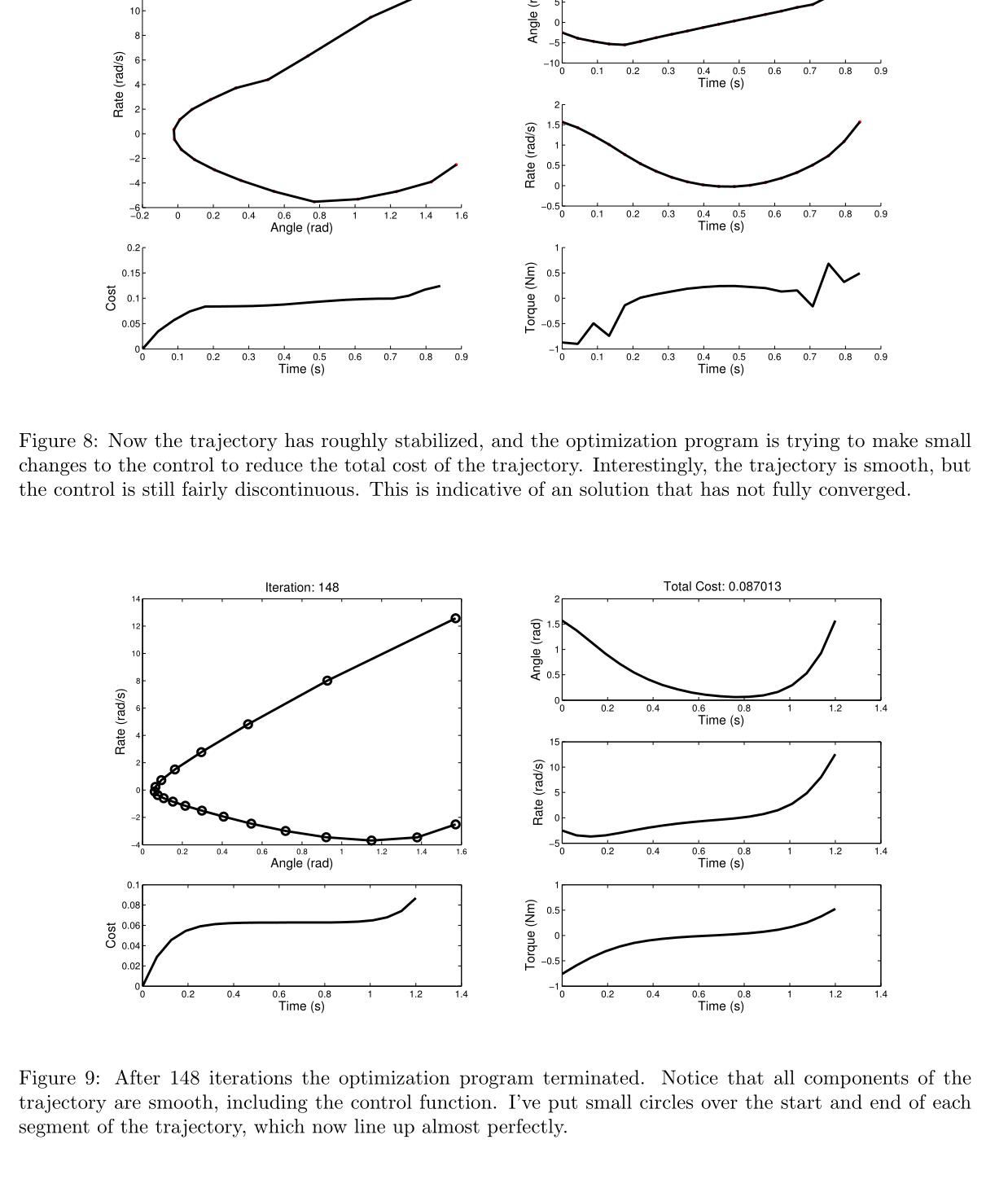
我创建了一个简单的示例来演示一个简单的多重射击转录算法(使用Matlab的FMINCON来解决底层优化)。在这个例子中，目标是为锤子找到一个周期性撞击表面的轨迹。锤被建模为点质量摆，并由扭矩源提供动力。使用转矩源的成本被建模为转矩平方对时间的积分。一系列的图显示了详细的进展，优化算法使朝着解决方案。在每张图的左边是状态空间轨迹的图。请注意，当铁锤撞击表面时，轨迹上有一个离散的跳跃。在这条轨迹的下面是一个图表，显示了成本函数是如何随时间累积的。在每个图的右侧是一组三个图，每个图都显示了轨迹对时间的单一组成部分(锤角、锤角速率和锤施加的扭矩)。最后一个图为状态空间轨迹中的每个网格点都有一个标记，并显示了最终的迭代次数。在第一张图中，轨迹是锯齿状的，有红色和黑色的线。红线表示轨迹中的缺陷——随着优化运行，这些缺陷变得任意小。运行这个例子的完整代码可以在我的网站上找到:http://ruina.tam.cornell.edu/research/MatthewKelly