网格贪吃蛇的降维度优化

Posted 2022-02-27 'or 1 or 不正经の泡泡

文章目录

• 前言
• 方案一将维
• 存在问题
• 解决方案

「这是我参与2022首次更文挑战的第28天，活动详情查看：2022首次更文挑战」

前言

今天早上，突然灵感一闪，好像想到了，先前我一直尝试把这个问题背包问题变形（蓝桥杯拿金币）与误区（网格贪吃蛇（求助））变成一个背包问题，这样我们就能够直接套公式去降低维度。但是的话这里有个问题就是那个豆子有可能在同一条直线上面，这样的话如果转化为背包问题，那么就出现了那个一个物品可能出现两个质量的情况，这样压根就优化不了。所以我们还是得回到我们的方案一上面。其实昨天晚上我是思考了三个方案来解决问题，第一个就是，点映射，降低多余浪费的空间矩阵，这样即使dp是二维的，但是范围也会大大缩小，同时时间复杂度也会降低，但是有个问题怎么映射，这里涉及到规划网格的问题。方案二，就是把这个点的区域进行划分，然后分区域dp，但是这样意味着我必须找到对角点，这个根本就不好找。最后就是方案三，这个其实是我想使用“虚拟二维数组的思想（这个是我以前刷Letcode的时候提出过的想法，当时是时间复杂度变高了，但是空间复杂度降低了）但是找不到好的逻辑映射关系”。并且在实际的运行过程当中，其实只有当前行，和上一行在dp，所以按照我们的套路其实是可以直接将维的，也就是分析前面的方案一（背包问题变形（蓝桥杯拿金币）与误区（网格贪吃蛇（求助）））

方案一将维

这个的话我们得看到我们方案一的思路。

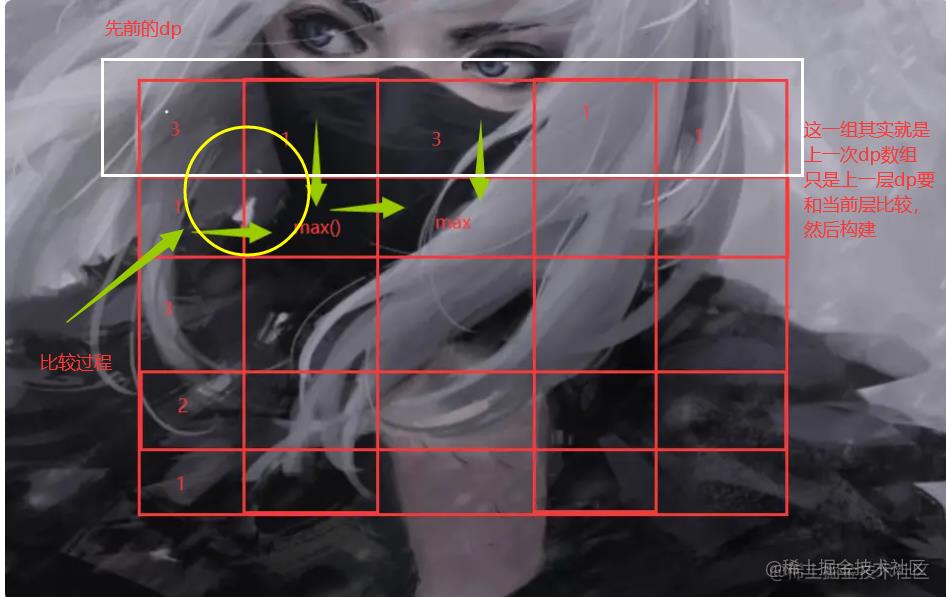
这样一来我们就可以得到中间状态的dp方程

dp[j] = Maxdp[j],dp[j-1]+当前层[j]

存在问题

理论上我们其实都是可以根据这个方式把那个原来的二维数组降低为一维数组的。
但是的话，在这道题目的问题在于啥，在于那个状态呀，我们的豆子是分布不均匀的，相当不均匀，所以在直接使用二维数组的时候，我们可以知道当前层有木有豆子，并且保存在dp二维数组里面，也就是原来的这段代码块。

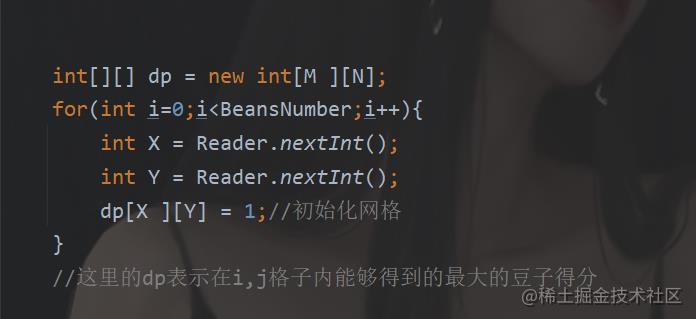
所以我们的问题就是如何能够保存到当前层的状态，知道这里面有木有豆子。
或者说，我们以前做的dp的初始化的时候都是直接在那个网格边缘进行初始化的，现在可不是这样，我们的豆子不一定在边缘。

解决方案

其实这个解决方案我当时已经想到了，但是我当时一直在想我的那个“虚拟二维数组解法”，其实我只需要转换思路直接用一维数组就行了。
那么如何解决列，就是用map存起来，代码如下

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStream;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Map;
import java.util.StringTokenizer;

class Main
    public static void main(String[] args) throws IOException 
        //获取初始化数据，这里对棋盘做了一个反转，从左上角到右下角
        //注意这里的X表示行，Y表示列

        Reader.init(System.in);
        int M = Reader.nextInt();
        int N = Reader.nextInt();
        int BeansNumber = Reader.nextInt();
        HashMap<Integer, ArrayList<Integer>> Beans = new HashMap<>();

        int[] dp = new int[N];//表示某一行的第j个格子能够获得的最大value

        for(int i=0;i<BeansNumber;i++)
            int X = Reader.nextInt();
            int Y = Reader.nextInt();

            if(Beans.containsKey(X))
                //存在个别点在同一条横线上
                ArrayList<Integer> templist = Beans.get(X);
                templist.add(Y);
                Beans.replace(X,templist);
            else 
                ArrayList<Integer> integers = new ArrayList<>();
                integers.add(Y);
                Beans.put(X, integers);
            
        
        //初始化，对第一行初始化
        MapFromBeans(Beans,dp,0);

        //进入中间状态
        for (int i=1;i<M;i++)
            int[] temp = new int[N];
            MapFromBeans(Beans,temp,i);
            for(int j=0;j<N;j++)
                if(j==0)
                    dp[j] = dp[j]+temp[j];
                else
                    dp[j] = Math.max(dp[j-1],dp[j])+temp[j];
                
            
        
        System.out.println(dp[N-1]);

    
    public static void MapFromBeans(Map<Integer,ArrayList<Integer>> Beans,int[] a,Integer key)
        if(Beans.containsKey(key))
            ArrayList<Integer> integers = Beans.get(key);
            for(Integer y:integers)
                a[y]=1;
            
        

    




class Reader 
    static BufferedReader reader;
    static StringTokenizer tokenizer;

    /**
     * call this method to initialize reader for InputStream
     */
    static void init(InputStream input) 
        reader = new BufferedReader(
                new InputStreamReader(input));
        tokenizer = new StringTokenizer("");
    

    /**
     * get next word
     */
    static String next() throws IOException 
        while (!tokenizer.hasMoreTokens()) 
            //TODO add check for eof if necessary
            tokenizer = new StringTokenizer(
                    reader.readLine());
        
        return tokenizer.nextToken();
    

    static int nextInt() throws IOException 
        return Integer.parseInt(next());
    

    static double nextDouble() throws IOException 
        return Double.parseDouble(next());
    

ok 问题解决。之后其实我们还能优化，因为你发现其实到头来还是只有几个点在dp，这里的方法其实和那个将维的思想类似，并且除了我们保存的豆子，其他的点都为0.当然这里就没啥太大必要了，因为这个时候又得判断时间复杂度又上去了，因为这个还是只拿到了8个，原来那个7个。

好了，那个28天活动做完了~