Carson带你学数据结构：归并排序，稳定性最高的排序算法

Posted 2022-02-26 Carson带你学Android

---

目录

---

1. 简介

属于 内排序算法中 的 归并排序类别

---

2. 算法原理

---

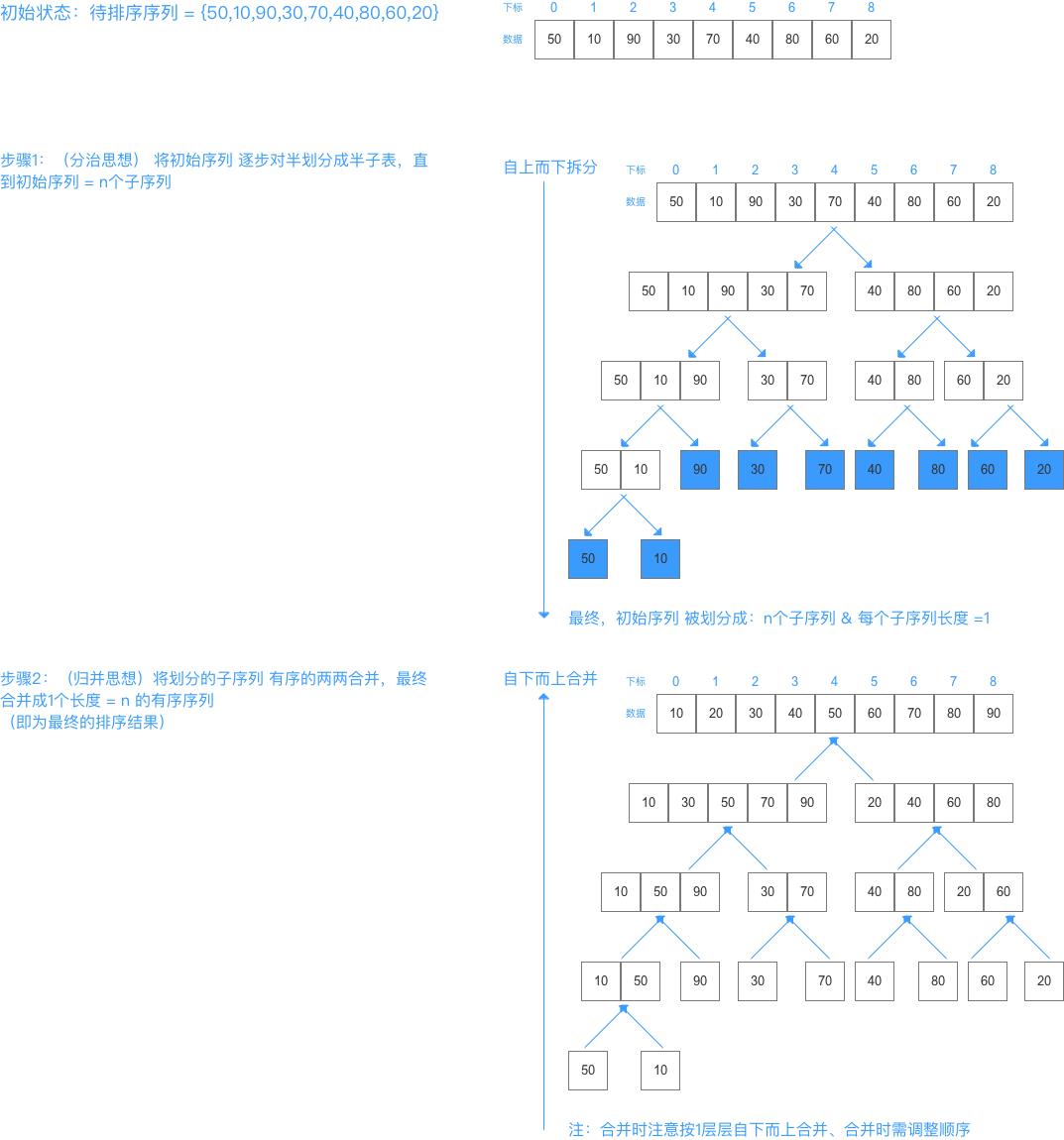
3. 算法示意图

---

4. 算法实现

有2种实现方式：递归 & 非递归方式

4.1 递归方式

• 具体请看注释

public class MergeSort 

    /**
     * 归并排序算法实现
     * 参数说明：
     * @param arr = 需排序的数组序列
     * @param low = 数组第1个元素下标
     * @param high = 数组最后1个元素下标
     */

    public static void mergeSort(int[] arr, int low, int high) 

        // 1. 计算出序列中间元素下标
        // 使用(low+high)/2 求中间位置容易溢出
        // 右移1位，相当于除以2，但右移的运算速度更快
        int mid = low + ( (high-low)>>1 );

        if (low < high) 
            // 2. （分治） 将初始序列 逐步对半划分成半子表，直到初始序列 = n个子序列
            // 通过 递归 实现
              // a. 左一半（第1个元素 - 中间元素）
              mergeSort(arr, low, mid);
              // b. 右一半（ 中间元素后1位 - 最后1个元素）
              mergeSort(arr, mid + 1, high);

            // 3. （归并）将划分的子序列 有序的两两合并,最终合并成1个长度 = n 的有序序列
            merge(arr, low, mid, high);
        

    

    /**
     * 归并排序算法中的有序合并序列 实现
     * 参数说明：
     * @param arr = 需排序的数组序列
     * @param low = 数组第1个元素 下标
     * @param mid = 数组中间元素 下标
     * @param high = 数组最后1个元素 下标
     */

    public static void merge(int[] arr, int low, int mid, int high) 

        // 1. 定义1个辅助数组用于存储结果
        int[] temp = new int[high - low + 1];

        int i = low; // 左指针，指向数组第1个元素 下标
        int j = mid + 1; // 右指针，指向数组中间元素的后1个下标
        int k = 0;

        // 2. 比较左、右两边的元素大小，将较小的数先移到新数组中
        while (i <= mid && j <= high) 
            if (arr[i] < arr[j]) 
                temp[k++] = arr[i++];
             else 
                temp[k++] = arr[j++];
            
        

        // 3. 把左边剩余的数移入新数组
        while (i <= mid) 
            temp[k++] = arr[i++];
        

        // 4. 把右边剩余的数移入新数组
        while (j <= high) 
            temp[k++] = arr[j++];
        

        // 5. 把新数组中的数覆盖到原有数组中
        for (int k2 = 0; k2 < temp.length; k2++) 
            arr[k2 + low] = temp[k2];
        
    

    /**
     * 执行 归并排序算法
     */
    public static void main(String[] args) 
        // 待排序序列
        int arr[] =  50, 10, 90, 30, 70, 40, 80, 60, 20 ;

        // 执行 归并排序序列
        mergeSort(arr, 0, arr.length - 1);

        // 输出排序后的序列
        for(int a =0;a<arr.length;a++)
            System.out.println(arr[a]);
    

• 测试结果

10
20
30
40
50
60
70
80
90

• Demo 地址
  Carson_Ho的Github地址：归并排序

4.2 非递归方式

• 具体请看注释

public class MergeSort 

    /**
     * 归并排序算法实现：非递归
     * 参数说明：
     * @param arr = 需排序的数组序列
     */

    public static void mergeSort(int[] arr) 

        int len = arr.length;
        int k = 1;

        while(k < len)
        
            MergePass(arr, k, len);
            k *= 2; // 一组组归并：1、2、4、8、16
        

    

    /**
     * 辅助算法
     * 作用：归并 数组中的相邻长度 = k的元素
     */

    private static void MergePass(int[] arr, int k, int n)
    
        int i = 0;
        int j;

        // 从前->后,将2个长度为k的子序列合并为1个
        while(i < n - 2*k + 1)
        
            merge(arr, i, i + k-1, i + 2*k - 1);
            // 参数2 = 距离长度
            // 参数3、4 = 合并的位置，如合并第1个 & 第2个位置的元素到新建的数组中
            i += 2*k;
        

        // 该代码的作用：保证将最后“落单”的、长度不足两两合并的部分 和 前面的合并起来
        if(i < n - k )
        
            merge(arr, i, i+k-1, n-1);
        

    

    /**
     * 归并排序算法中的有序合并序列 实现
     * 参数说明：
     * @param arr = 需排序的数组序列
     */

    public static void merge(int[] arr, int low, int mid, int high) 

        // 辅助数组 = 暂存合并的结果
        int[] temp = new int[high - low + 1];

        int i = low; // 左指针
        int j = mid + 1; // 右指针
        int k = 0;

        // 把较小的数先移到新数组中
        while (i <= mid && j <= high) 
            if (arr[i] < arr[j]) 
                temp[k++] = arr[i++];
             else 
                temp[k++] = arr[j++];
            
        
        // 把左边剩余的数移入数组
        while (i <= mid) 
            temp[k++] = arr[i++];
        
        // 把右边剩余的数移入数组
        while (j <= high) 
            temp[k++] = arr[j++];
        
        // 把新数组中的数覆盖nums数组
        for (int k2 = 0; k2 < temp.length; k2++) 
            arr[k2 + low] = temp[k2];
        
    

    /**
     * 执行 归并排序算法

     */
    public static void main(String[] args) 
        // 待排序序列
        int arr[] =  50, 10, 90, 30, 70, 40, 80, 60, 20 ;

        // 执行 归并排序序列
        mergeSort(arr);

        // 输出排序后的序列
        for(int a =0;a<arr.length;a++)
            System.out.println(arr[a]);

    

• 测试结果

10
20
30
40
50
60
70
80
90

---

5. 性能分析

以下将分析算法的性能：时间复杂度、空间复杂度、稳定性

---

6. 总结

• 对于递归方式：实现简洁 & 易理解，但会造成空间上的性能损耗 = 递归时深度为log2n的栈空间
• 对于非递归方式：a. 做法更加直接（从最小的序列开始规定 & 直到完成，递归方式 = 先拆分递归，再归并退出递归）；b. 空间性能少，不需递归时深度为log2n的栈空间
• 所以，实现归并时 推荐使用非递归方法

---

Carson带你学数据结构系列文章：
Carson带你学数据：线性表-数组、链表
Carson带你学数据：特殊的线性表-栈、队列
Carson带你学数据：串
Carson带你学数据：树
Carson带你学数据：二叉树
Carson带你学数据：图
Carson带你学数据：查找

---

欢迎关注Carson_Ho的CSDN博客 ！

博客链接：https://carsonho.blog.csdn.net/

---

请点赞！因为你的鼓励是我写作的最大动力！