知识表示方法

Posted 2023-02-16 程序媛小哨

人工智能原理——第二章 知识表示方法

文章目录

• 人工智能原理——第二章 知识表示方法
• • 2.1 知识与知识表示的概念
  • • 2.1.1 知识
    • • 1.什么是知识？
      • 2.数据、信息、知识及其关系
      • 3.知识的类型
      • 4.知识的特性
      • 5.人工智能系统所关心的知识
    • 2.1.2 知识表示的概念
    • • 1.什么是知识表示
      • 2.知识表示的两种基本观点
      • 3.知识表示方法
  • 2.2 谓词逻辑表示法
  • • • 2.2.1一阶谓词的逻辑学基础
      • • 命题（proposition）
        • 命题的真值：
        • • 命题类型
        • 命题逻辑词
        • 语法
        • 定义
        • 论域：
        • 谓词：
        • 函数：
        • 谓词逻辑组成
      • 2.2.2 连接词
      • • 1.合取(与)
        • 2.析取（或）
        • 3.否定（非）
    • 2.2.3 约束量词
    • • 2.2.4 谓词公式
      • • 1.项（Item）
        • 2.原子谓词公式（原子公式）
        • 3.谓词公式（合式）
        • 4.量词的辖域
        • 5.约束变元：
        • 6.自由变元：
        • 7.变元的换名：
        • 8.谓词公式真值表
      • 2.2.5 谓词公式性质
      • • 谓词公式的等价公式
        • 谓词逻辑表示步骤：
      • 2.2.7 谓词逻辑表示的应用
      • • 1.机器人搬箱子
        • 2.猴子和香蕉问题 ( Monkey and Banana Problem )
  • 2.2 谓词逻辑表示法小结
  • 2.3 产生式表示法
  • • 1.产生式规则（Production Rule）
    • 2.产生式的含义和作用
    • 3.产生式与逻辑蕴涵（逻辑规则）的异同：
    • 4.产生式与条件语句的主要区别：
    • 5.产生式表示实例

2.1 知识与知识表示的概念

2.1.1 知识

1.什么是知识？

• 知识是人们在改造客观世界的实践中积累起来的认识和经验。
• 认识：包括对事物现象、本质、属性、状态、关系、联系和运动等的认识
• 经验：包括解决问题的微观方法：如步骤、操作、规则、过程、技巧等。宏观方法：如战略、战术、计谋、策略等。

知识的有代表性的定义
（1）Feigenbaum: 知识是经过剪裁、塑造、解释、选择和转换了的信息
（2）Bernstein：知识由特定领域的描述、关系和过程组成
（3）Heyes-Roth：知识=事实+信念+启发式

2.数据、信息、知识及其关系

数据是信息的载体，本身无确切含义，其关联构成信息。
信息是数据的关联，赋予数据特定的含义，仅可理解为描述性知识。

知识可以是对信息的关联，也可以是对已有知识的再认识

• 常用的关联方式： if …… then ……
• 知识在信息的基础上增加了上下文信息，提供了更多的意义因此也就更加有用和有价值。
• 知识是随着时间的变化而动态变化的，新的
• 知识可以根据规则和已有的知识推导出来。
• 因此可以认为知识是经过加工的信息，它包括事实、信念和启发式规则。
• 关于知识的研究称为认识论（Epistemology），它涉及知识的本质、结构和起源。

3.知识的类型

(1) 按知识的性质
概念、命题、公理、定理、规则和方法
(2) 按知识的作用域

• 常识性知识：通用通识的知识。人们普遍知道的、适应所有领域的知识。
• 领域性知识：面向某个具体专业领域的知识。例如：专家经验。
  (3) 按知识的作用效果
• 事实性知识：用于描述事物的概念、定义、属性等；或用于描述问题的状态、环境、条件等。
• 过程性知识：用于问题求解过程的操作、演算和行为的知识；
  用来指出如何使用那些与问题有关的事实性知识的知识；
  表示方式：产生式、谓词、语义网络等。
• 控制性知识：(元知识或超知识)
  是关于如何使用过程性知识的知识；
  例如：推理策略、搜索策略、不确定性的传播策略。

(4) 按知识的层次

• 表层知识：描述客观事物的现象的知识。例如：感性、事实性知识
  -深层知识：描述客观事物本质、内涵等的知识。例如：理论知识

(5)按知识的确定性

• 确定性知识：可以说明其真值为真或为假的知识
• 不确定性知识：包括不精确、模糊、不完备知识

不精确：知识本身有真假，但由于认识水平限制却不能肯定其真假表示：用可信度、概率等描述

模 糊：知识本身的边界就是不清楚的。例如：大，小等表示：用可能性、隶属度来描述

不完备：解决问题时不具备解决该问题的全部知识。例如：医生看病

(6) 按知识的等级

• 零级知识：叙述性知识
• 一级知识：过程性知识
• 二级知识：控制性知识（元知识或超知识）

4.知识的特性

• 相对正确性
  在一定的条件及环境下，知识一般是正确的，可信任的
• 不确定性
  由随机性引起的不确定性
  由模糊性引起的不确定性
  由不完全性引起的不确定性
  由经验性引起的不确定性
• 可表示性和可利用性
  知识是可以表示出来的
  知识是可以利用的
• 相对稳定和持久性

5.人工智能系统所关心的知识

一个Agent需要什么样的知识才可能具有智能呢？一般说来至少包括下面几个方面的知识

• 事实：
  是关于对象和物体的知识。
• 规则：
  是有关问题中与事物的行动、动作相联系的因果关系的知识，是动态的，常以“如果……那么……”形式出现。
• 元知识：
  是有关知识的知识，是知识库中的高层知识。例如包括怎样使用规则、解释规则、校验规则、解释程序结构等知识。
• 常识性知识：
  泛指普遍存在而普遍认识了的客观事实一类知识，即指人们共有的知识。

2.1.2 知识表示的概念

1.什么是知识表示

  是对知识的描述，即用一组符号把知识编码成计算机可以接受的某种结构。其表示方法不唯一。

知识表示的要求

• 表示能力：能否正确、有效地表示问题。包括：
  1)表示范围的广泛性
  2)领域知识表示的高效性
  3)对非确定性知识表示的支持程度
• 可利用性：可利用这些知识进行有效推理。包括：
  1)对推理的适应性：推理是根据已知事实利用知识导出结果的过程
  2)对高效算法的支持程度：知识表示要有较高的处理效率
• 可实现性：要便于计算机直接对其进行处理
• 可组织性：可以按某种方式把知识组织成某种知识结构
• 可维护性：便于对知识的增、删、改等操作
• 自然性： 符合人们的日常习惯
• 可理解性：知识应易读、易懂、易获取等

2.知识表示的两种基本观点

• 叙述性的观点：
  将知识的表示和知识的运用分开处理，在知识表示时不涉及如何运用知识的问题。
• 过程性的观点：
  将知识的表示和知识的运用结合起来，知识包含于程序之中。

3.知识表示方法

(1)非结构化方法
谓词逻辑表示法
产生式系统表示法
过程表示法
…
(2)结构化方法
语义网络表示法
框架表示法
…

1. 谓词逻辑表示法
   采用一阶谓词逻辑表示知识，是一种叙述性的知识表示方法，它的推理机制是采用归结原理，主要用于自动定理证明。

2. 状态空间表示法
   把求解的问题表示成问题状态、操作、约束、初始状态和目标状态。问题的求解过程就可以看成是问题状态在状态空间的移动过程。

3. 产生式规则 把知识表示成“模式-动作”对，表示方式自然、简洁。 它的推理机制以演绎推理为基础。目前已是专家系统中使用最广泛的一种表示方式，一般将这种系统称为基于规则的系统。

4. 语义网络 由结点和结点之间的弧组成，结点表示概念(事件、事物)，弧表示它们之间的关系。目前语义网络已广泛用于基于知识的系统。在专家系统中，常与产生式规则一起共同表示知识。

5. 框架 将知识表示成高度模状化的结构。框架是把关于一个对象或概念的所有信息和知识都存储在一起的一种数据结构。框架的层次结构可以表示对象之间的相互关系，用框架表示知识的系统称为基于框架的系统。在专家系统中，框架也常常和产生式规则一起共同表示知识。6. 概念从属
   表示自然语言语义的一种理论，它的特点是便于根据语句进行推理，而且与语句本身所用的语言无关。 概念从属表示的单元并不对应于语句中的单词，而是能组合成词义的概念单元。

6. 脚本（剧本） 脚本用于描述固定的事件序列。 强调事件之间的因果关系/因果链。 与框架类似，但是，框架是一种通用的结构而脚本则对某些专门知识更为有效。

7. Petri网 能很好地模拟异步并行操作,所以在并行处理和分布式计算机领域中应用较多,主要作为模拟用的数学工具。 利用Petri网可以模拟逻辑运算、语义网、框架、与或图、状态空间与规则等多种功能,因此也可以作为一种通用的知识表示形式。

8. 面向对象

2.2 谓词逻辑表示法

一阶谓词逻辑表示法是一种基于数理逻辑的表示方法。
数理逻辑是一门研究推理的学科。可分为：

• 一阶经典逻辑：一阶经典命题逻辑，一阶经典谓词逻辑
• 非一阶经典逻辑：指除经典逻辑以外的那些逻辑，例如：二阶逻辑，多值逻辑，模糊逻辑等。

本节主要讨论

• 一阶谓词逻辑表示的逻辑学基础
  1)命题和真值；论域和谓词；连词和量词；
  2)项与合式公式；自由变元与约束变元
• 谓词逻辑表示方法
• 谓词逻辑表示的应用
• 谓词逻辑表示的特性

2.2.1一阶谓词的逻辑学基础

谓词逻辑是一种重要的知识表示方法，是目前为止能够表示人类思维活动规律的一种最精确的形式语言，是知识的形式化表示，定理自动证明等研究的基础。
谓词逻辑基于命题逻辑，包含了整个命题逻辑的概念。

命题（proposition）

命题的定义：
  断言：一个陈述句称为一个断言.
  命题：具有真假意义的断言称为命题.

命题就是具有真假意义的陈述句。如“雪是黑的”，“3 < 5”。
一个命题具有一个值，叫真值。真值有“真”和“假”两种，符号分别是T和F。
命题可以在一种情况下为真，另一种情况下为假(如1+1=2和1+1=10)

命题的真值：

   T：表示命题的意义为真
   F：表示命题的意义为假

命题真值的说明
一个命题不能同时既为真又为假
一个命题可在一定条件下为真，而在另一条件下为假
薛定谔的猫

命题类型

• 原子命题 – 不能分解成更简单的陈述语句。
• 复合命题 – 由连接词、标点符号和原子命题等符合构成的命题。
  （注：所有命题都有真假）

命题逻辑词

通常用大写字母P,Q,R,S等来表示命题。 如：
P ---- 今天下雪
P就是“今天下雪”这个命题的名，也称为命题标识符。

• 命题常量：如果一个命题标识符表示确定的命题，就称为命题常量。

• 命题变元：如果命题标识符只表示任意命题的位置标志，就称为命题变元。
  

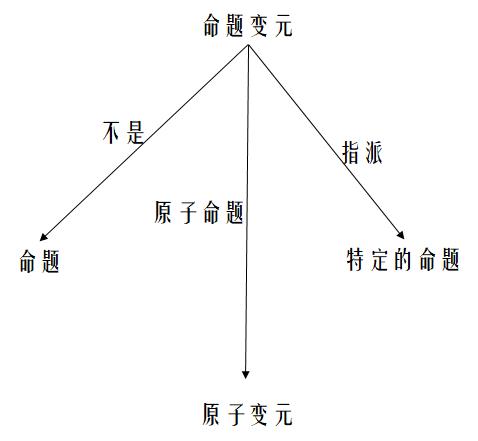
语法

命题常元： True（T）和False（F）
命题符号： P,Q,R,T等
连接词：¬ ∨∧→
括号： （）

命题逻辑主要使用上述5个连接词，通过这些连接词，可以由简单的命题构成复杂的复合命题。

定义

¬ ：否定， 复合命题¬Q表示否定Q的真值命题，即“非Q”
∧：合取，复合命题P∧Q表示P和Q的合取，即“P与Q”
∨：析取，复合命题P∨Q表示P和Q的合取，即“P或Q”
→：条件，复合命题P →Q表示命题P是命题Q的条件，即“如果P，那么Q”
↔：双条件，复合命题P Q表示命题P，命题Q互相作为条件，即“如果P那么Q, 如果Q那么P”

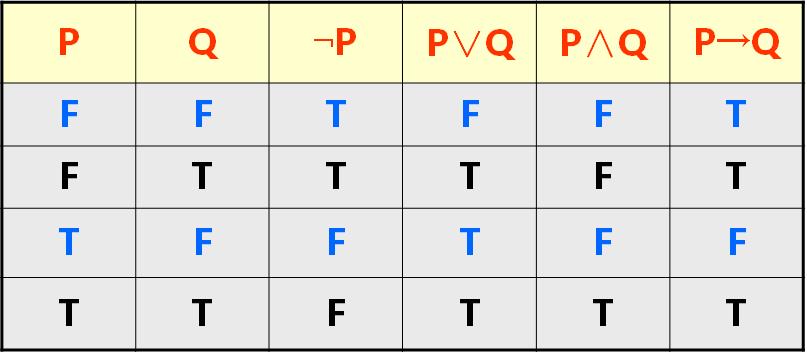
连接词功能真值表

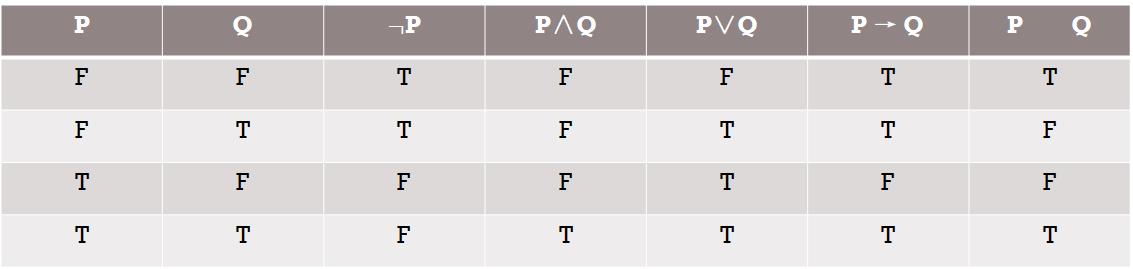
命题逻辑的栗子

P：老李是小李的爸爸
L：中国的首都是北京

但是 “老李和小李”，“中国和北京”的关系在命题逻辑里体现不出来，于是就需要谓词逻辑。

谓词逻辑是一种形式语言，更接近自然语言，又方便存入计算机处理。

谓词逻辑的形式：
P（𝑡_1,𝑡_2, …,𝑡_n），𝑡_1,𝑡_2,…,𝑡_n是个体，把某个事物，人，概念放到括号里，P叫做谓词名。 用来刻画个体的性质，状态和个体间的关系，就叫谓词。

论域：

由所讨论对象的全体构成的集合。亦称为个体域。（类似定义域）。

• 个体：论域中的元素。

谓词：

在谓词逻辑中命题是用形如 P(x1,x2,…,xn) 的谓词来表示，其中：

• 谓词名P ：是命题的谓语，表示个体的性质、状态或个体之间的关系
• 个体x1,x2,…,xn ：是命题的主语，表示独立存在的事物或概念

设D是个体域，P：Dn→T，F｝是一个映射，其中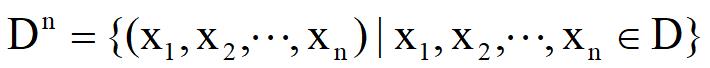

则称P是一个n元谓词，记为P(x1,x2,…,xn)，其中，x1,x2,…,xn 为个体，可以是个体常量、变元和函数。
例如：
GREATER(x,6) x大于6
TEACHER(father(Wang Hong)) 王宏的父亲是一位教师

函数：

设D是个体域，f：Dn→D是一个映射，其中

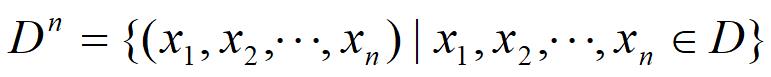
则称f是D上的一个n元函数，记作 f(x1,x2,…,xn)

谓词与函数的区别：

• 谓词是 Dn 到T，F的映射，函数是Dn到D的映射
• 谓词的真值是T和F，函数的值（无真值）是D中的元素
• 谓词可独立存在，函数只能作为谓词的个体

e.g.
小李的父亲老李是老司机
DRIVER( FATHER ( XIAOLI ) )
FATHER – 函数，没有真值

谓词逻辑组成

• 谓词符号
• 变量符号
• 常量符号
• 函数符号
• 其他辅助符号——括号、标点符号等。
  

谓词里面包含谓词，就成了二阶谓词

老李在阿里巴巴当工程师

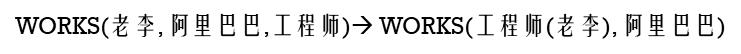
就是一个二阶谓词了，其中“工程师(老李)”是一阶谓词，也是个体。

2.2.2 连接词

1.合取(与)

• 符号：∧
• 定义：A ∧ B 为真，当且仅当A、B同时为真。
• 例子：
  ① 我喜欢音乐和绘画。
  LIKE（ I，Music ）∧ LIKE( I, Painting )——同时性
  ② 李住在一幢黄色的房子里。
  LIVES(Li, House1）∧ COLOR(House1, Yellow)——同时性

2.析取（或）

• 符号：∨
• 定义：A ∨ B为假，当且仅当A、B同时为假。
• 例子：李明打篮球或踢足球。
  PLAYS（LiMing,Basketball）∨ PLAYS（LiMing,Football）
  排斥或(异或)：一种可能发生，另一种可能性不可能发生的情形。

例如：
李现在在教室，或在实验室。
——李在教室，就不可能在实验室；
反之亦然。

3.否定（非）

• 符号：﹁ 、∽
• 定义：﹁ A为真，当且仅当A为假。
• 例子：机器人不在2号房间里。
  ﹁ INROOM（Robot,Room2）

排斥或例子：李现在在教室，或在操场。
[ IN(Li,Classroom) ∧ ﹁ IN(Li,Field)] ∨ [﹁ IN(Li,Classroom) ∧ IN(Li,Field)]
----李在教室，不在操场；李在操场，不在教室

4.蕴涵

• 符号：→， =>
• 定义：A → B为假，当且仅当A为真，B为假。
• 等价式： ﹁A ∨ B
• 表达语义：如果A，则B。
• 例子：如果刘华跑得最快，那么他取得冠军。
  RUNS(LiuHua,Fastest) →WINS(LiuHua,Champion)

连词的优先级（不加括号）
¬,∧,∨,→

2.2.3 约束量词

约束量词，简称为量词，用来约束逻辑变元在其论域中的取值方式。

2.2.4 谓词公式

1.项（Item）

(1) 个体常量、个体变量是项；
(2) 若t1,t2,…,tn是项，f是n元函数，则f(t1,t2,…,tn)是项；
(3) 由(1)、(2)生成的表达式是项。
通俗地说：个体常量、个体变量和函数统称为项。

2.原子谓词公式（原子公式）

若t1,t2,…,tn是项，P是谓词，则称P(t1,t2,…,tn)为原子谓词公式。

3.谓词公式（合式）

• (1) 原子公式是谓词公式；
• (2) 若A是谓词公式，则¬A也是谓词公式；
• (3) 若A,B是谓词公式，则A∨B，A∧B，A→B也都是谓词公式；renyix
• (4) 若A是谓词公式，x是项，则
  都是谓词公式。
• (5) 按（1）—（4）规则构造的表达式是谓词公式。
  例如：
  
  都是谓词公式。

4.量词的辖域

量词的约束范围，即指位于量词后面的单个谓词或者用括弧括起来的合式公式。
例：

5.约束变元：

受到量词约束的变元，即辖域内与量词中同名的变元称为约束变元

6.自由变元：

不受约束的变元称为自由变元
e.g.

7.变元的换名：

谓词公式中的变元可以换名。要保持变量的论域不变。此外还需注意：

1. 对约束变元，必须把同名的约束变元都统一换成另外一个相同的名字，且不能与辖域内的自由变元同名。
   例：

2. 对辖域内的自由变元，不能改成与约束变元相同的名字。
   例：

3. 存在量词约束的变量换名同上。

8.谓词公式真值表

取出公式中所有单个谓词，按所有可能的取值组合，再按连接词和量词的定义给出合适公式的真值。

2.2.5 谓词公式性质

谓词公式的等价公式

• 两个谓词公式，无论如何解释，若两者的真值表相同，则两公式为等价谓词公式。
  
  
  

谓词逻辑表示步骤：

• (1) 先根据要表示的知识定义谓词
• (2) 再用连词、量词把这些谓词连接起来

2.2.7 谓词逻辑表示的应用

1.机器人搬箱子

机器人robot，箱子box，2个桌子a和b。初始状态机器人位于c处，空手，box在a上。
目标：机器人把位于a上的box搬运到b上。

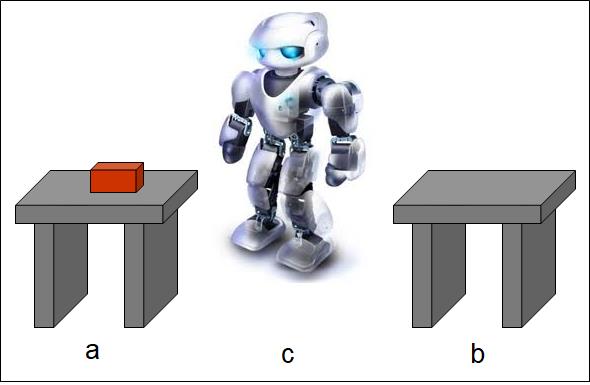
机器人行动的目标是把问题的初始状态转换为目标状态，而要实现问题状态的转换需要完成一系列的操作

为啥不把桌子也作为个体呢，因为桌子有a,b两个，a,b为个体，桌子是类别，机器人robot和box只有一个，直接用它做个体

定义描述操作的谓词：

• 条件部分：用来说明执行该操作必须具备的
  先决条件，可用谓词公式来表示
• 动作部分：给出该操作对问题状态的改变情况，通过在执行该操作前的问题状态中删去和增加相应的谓词来实现
• 需要定义的操作：
  ①Goto(x, y)：从x处走到y处。
  ②Pickup(x)：在x处拿起盒子。
  ③Setdown(y)：在y处放下盒子。

各操作的条件和动作：

机器人每执行一操作前，都要检查该操作的先决条件是否可以满足。如果满足，就执行相应的操作；否则再检查下一个操作。

2.猴子和香蕉问题 ( Monkey and Banana Problem )

在房间的 a 处有一只猴子，b 处有一个箱子，c 处挂着一串香蕉，猴子欲想拿取香蕉，他必须首先走到 b 处，推动箱子到 c 处，然后爬上箱子才可以办到。假设猴子和箱子都只做一维运动。用谓词逻辑表示的状态空间求解此问题。

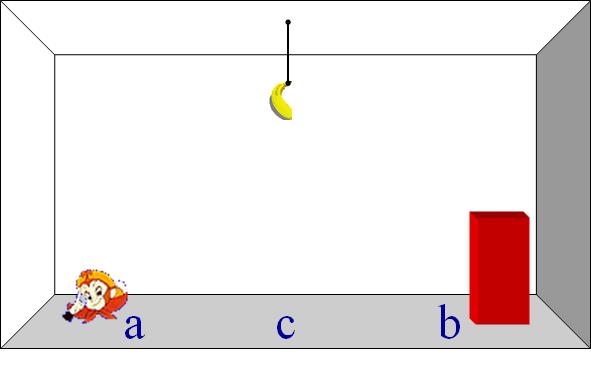
逻辑表示是推理的基础，后面推理部分还将介绍更多的内容。

2.2 谓词逻辑表示法小结

主要优点

• 自然：一阶谓词逻辑是一种接近于自然语言的形式语言系统，谓词逻辑表示法接近于人们对问题的直观理解
• 明确：有一种标准的知识解释方法，因此用这种方法表示的知识明确、易于理解
• 精确：谓词逻辑的真值只有“T”与“F”，其表示、推理都是精确的
• 灵活：知识和处理知识的程序是分开的，无须考虑处理知识的细节
• 模块化：知识之间相对独立，这种模块性使得添加、删除、修改知识比较容易进行

主要缺点

• 知识表示能力差：只能表示确定性知识，而不能表示非确定性知识、过程性知识和启发式知识
• 知识库管理困难：缺乏知识的组织原则，知识库管理比较困难
• 存在组合爆炸：由于难以表示启发式知识，因此只能盲目地使用推理规则，这样当系统知识量较大时，容易发生组合爆炸
• 系统效率低：它把推理演算与知识含义截然分开，抛弃了表达内容中所含有的语义信息，往往使推理过程冗长，降低了系统效率

2.3 产生式表示法

产生式（Production）是目前人工智能中使用最多的一种知识表示方法。本节主要内容：

• 产生式规则
• 产生式与蕴含式的异同
• 产生式与条件语句的区别

1943年，逻辑学家 Post 首提，用于计算形式体系中的符号串替换运算。认为，任何数学或逻辑系统都可以简化为一些列规则，在规则中制定如何把一个符号串变成另一个符号串，即给定一个输入符号串通过产生式规则可产生另一符号串，而不管符号串的物理意义。

1.产生式规则（Production Rule）

形如： P→Q              或者
      IF  P  THEN Q    或者
      如果 P，那么 Q
的语句叫做一条产生式规则。

其中:

• P — 叫做：前件、前项、左边(LHS-left hand side)
  它给出了该产生式可否使用的前提条件，由事实的逻辑组合来构成；
• Q — 叫做：后件、后项、右边(RHS-right hand side）
  它指出当前提P满足时，应该推导出的结论或应该执行的动作。

2.产生式的含义和作用

• 含义：如果前提P满足，则可推出结论Q或执行Q所规定的操作。
• 作用：产生式规则用来表示问题领域的一般知识。
  

3.产生式与逻辑蕴涵（逻辑规则）的异同：

• 逻辑规则的两边只能是命题或谓词，产生式可以是命题和谓词，也可以是其他符号串；
• 逻辑规则要满足真值表，即前后件最终只能为T或F。产生式前后件都可以是任意类型的值，产生式规则右边可能是动作，甚至是复杂的过程语句；
• 产生式可以处理不确定性，逻辑规则只能用于确定推理；
• 逻辑规则可以视为产生式规则，反之不然；
• 形式相同，产生式应用范围更广。

4.产生式与条件语句的主要区别：

(1) 前项结构不同

• 产生式的前项可以是一个复杂的的结构，其值不一定为逻辑类型；
• 传统程序设计语言中if的左部仅仅是一个布尔表达式

(2) 控制流程不同

• 产生式系统中满足前提条件的规则被激活后，不一定被立即执行，能否执行将取决于冲突消解策略
• 传统程序设计语言中是严格地从一个条件语句向其下一个条件语句传递。

5.产生式表示实例

【例2.3.3】 设有3个传教士和3个野人来到一条河的左岸，打算乘一只船从左岸渡到右岸去。该船的负载能力为2人。在任何时候，如果野人人数超过传教士人数，那么野人就会把传教士吃掉。野人绝对服从传教士的指挥和调度。