数据机构与算法之深入解析“解码方法”的求解思路与算法示例

Posted 2022-02-21 Serendipity·y

一、题目要求

• 一条包含字母 A-Z 的消息通过以下映射进行编码：

'A' -> "1"
'B' -> "2"
...
'Z' -> "26"

• 要解码已编码的消息，所有数字必须基于上述映射的方法，反向映射回字母（可能有多种方法）。例如，“11106” 可以映射为：
• • “AAJF” ，将消息分组为 (1 1 10 6)；
• • “KJF” ，将消息分组为 (11 10 6)。
• 注意，消息不能分组为 (1 11 06) ，因为 “06” 不能映射为 “F” ，这是由于 “6” 和 “06” 在映射中并不等价。
• 给你一个只含数字的非空字符串 s ，请计算并返回解码方法的总数 。
• 题目数据保证答案肯定是一个 32 位的整数。
• 示例 1：

输入：s = "12"
输出：2
解释：它可以解码为 "AB"（1 2）或者 "L"（12）。

• 示例 2：

输入：s = "226"
输出：3
解释：它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。

• 示例 3：

输入：s = "0"
输出：0
解释：没有字符映射到以 0 开头的数字。
含有 0 的有效映射是 'J' -> "10" 和 'T'-> "20" 。
由于没有字符，因此没有有效的方法对此进行解码，因为所有数字都需要映射。

• 提示：
• • 1 <= s.length <= 100；
• • s 只包含数字，并且可能包含前导零。

二、求解算法

① 暴力递归（超时）

• 枚举所有可能的解码方案，枚举方法如下：
• • 首先对 1、……、26 一共 26 个数字，可以构建一个编码的字符串集合 legalstr；
• • 对于任意的字符串，依次选择开始的 1 个字符或者开始的 2 个字符进行解码。
• • • 如果这 1 字符或者 2 个字符在 legalstr 中，则表示可以编码，对剩下的字符串执行同样的操作；
• • • 如果不合法，就不能生出递归树的枝叶。
• 当剩余字符串长度为 0 的时候就说明完成了解码，给计数器加 1。
• 假设字符串长为 n，递归树如下图所示：

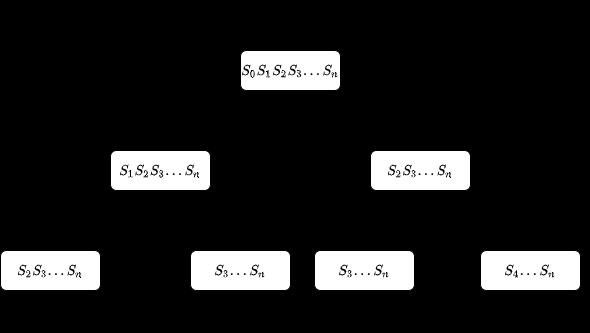
• Python 示例：

class Solution:
    def numDecodings(self, s: str) -> int:
        legalstr = set(str(i) for i in range(1, 27))
        self.ans = 0
        def dfs(s):
            if len(s)==0:
                self.ans += 1
                return 
            # 对于任何一个字符串，我们每次可以读取一到两个
            if s[0] in legalstr:
                dfs(s[1 : ])
            if len(s)>1 and s[ : 2] in legalstr:
                dfs(s[2 : ])
            return
        dfs(s)
        return self.ans

from functools import lru_cache
class Solution:
    @lru_cache(None)
    def numDecodings(self, s: str) -> int:
        if s and int(s[0]) == 0:
            return 0
        if len(s) <= 1:
            return 1
        if int(s[:2]) <= 26:
            return self.numDecodings(s[1:]) + self.numDecodings(s[2:])
        return self.numDecodings(s[1:])

• 暴力枚举超时的原因是：不仅计算了结果，还求出了每一种可能的编码，并且在求解问题的过程中，重复计算了子问题（如图中字符串 S₂S₃S₄…S_n 和 S₃S₄…S_n 至少出现了两次）。

② 动态规划

• 确定动态规划 dp 数组的定义：
• • 设 dp[i] 为 s[0…i] 字符串有多少种解码方法，动态规划 dp[i] 的定义如果是题目所问，则返回的结果就是最后一个状态值 dp[-1]。
• 确定状态转移方程：
• • 状态转移方程表示了大规模的问题如何由小规模问题转换而来，即状态转移方程表达了不同规模的子问题之间的关系，所以思考的方向是：此时 dp[i] 可以如何利用 dp[i - 1]、…、dp[0]。
• 对 2 个字符，可能解码成 0 种、1 种、2 种情况，所以需要进行分类讨论这 2 个字符什么时候解码成 0 种，什么时候解码成 1 种，什么时候解码成 2 种。利用我们一开始设置的合法集合（legalstr）可以很快的判断出这 2 个字符连起来是否可解码以及分开时是否可以分别解码的，从而得出解码方案数。分类讨论具体如下：
• • s[i] 不在合法集合中，也就是 s[i] 为 0 的情况：
• • • s[i - 1] + s[i] = s[i - 1: i + 1] 也不在合法集合中（比如 00）：无法解码字符串，直接返回 0；
• • • s[i - 1: i + 1] 在合法集合中（比如 10）：s[i - 1: i + 1] 只有一种解码可能，所以 s[i - 1: i + 1] 的解码是固定的，dp[i] = dp[i - 2] 也就是到 i 的解码方案 = 到 i-2 的解码方案，因为 i-1 到 i 的位置是确定的。
• • s[i] 在合法集合中：
• • • s[i - 1: i + 1] 不在合法集合中（比如 31）：s[i - 1: i + 1] 无法解码，s[i] 单独解码,所以 dp[i] = dp[i - 1]；
• • • s[i - 1: i + 1] 在合法集合中（比如 21）：这种时候 s[i - 1: i + 1] 可以解码，也可以拆开分别解码，那么这两种不同的解码会导致之后的整体解码都是不同的，所以 dp[i] = dp[i - 2] + dp[i - 1]。
• 由于状态转移方程需要 dp[i - 2] ，所以我们初始化的时候要初始化 dp[0] 和 dp[1] , dp[1] 表示两个字符的解码方案，此时有三种可能性，所以也要分类讨论。
• Python 示例：

class Solution:
    def numDecodings(self, s: str) -> int:
        if s[0] == '0': return 0
        if len(s) == 1: return 1
 
        legalstr = set(str(i) for i in range(1, 27))
 
        dp = [0] * (len(s))
        dp[0] = 1 
        if s[1] not in legalstr:  # s[1]为0
            dp[1] = 1 if s[ : 2] in legalstr else 0
        else:
             dp[1] = 2 if s[ : 2] in legalstr else 1            
 
        # 因为要用到i-2 所以至少初始化 dp[0] dp[1]
        for i in range(2, len(s)):
            if s[i] not in legalstr:
                if s[i - 1: i + 1] not in legalstr:
                    return 0
                else:
                    dp[i] = dp[i - 2]
            else:
                if s[i - 1: i + 1] in legalstr:
                    dp[i] = dp[i - 1]+dp[i - 2]
                else:
                    dp[i] = dp[i - 1]
        return dp[-1]

• 因为 dp[1] 的生成要分类讨论 s[1] 和 s[ : 2] 的情况，比较繁琐。 所以在开头加一个虚拟数字 9(3-9) 不影响结果，这个时候 dp[0] = 1，如果过了一开始的特判 if s[0] == ‘0’: return 0 ，dp[1] = 1。因此 Python 优化示例：

class Solution:
    def numDecodings(self, s: str) -> int:
        if s[0] == '0': return 0
        if len(s) == 1: return 1
 
        legalstr = set(str(i) for i in range(1, 27))
 
        dp = [0] * (len(s) + 1)
        dp[0] = 1 
        dp[1] = 1
 
        for i in range(1, len(s)):
            if s[i] not in legalstr:
                if s[i - 1: i + 1] not in legalstr:
                    return 0
                else:
                    dp[i + 1] = dp[i - 2 + 1] # 因为dp多了一个，所以集体加1
            else:
                if s[i - 1: i + 1] in legalstr:
                    dp[i + 1] = dp[i - 1 + 1]+dp[i - 2 + 1]
                else:
                    dp[i + 1] = dp[i - 1 + 1]
        return dp[-1]

• 可以有更节省空间的做法，那就是：滚动数组，方法就是把上面的 dp[i - 1] dp[i] dp[i + 1] 换成 a b c，每次循环结束的时候 a 变成 b， b 变成 c，也就是滚动起来。因此 Python 优化示例：

class Solution:
    def numDecodings(self, s: str) -> int:
        if s[0] == '0':return 0
        if len(s) == 1:return 1
 
        legalstr = set(str(i) for i in range(1, 27))
 
        a = 1 
        b = 1
 
        for i in range(1, len(s)):
            if s[i] not in legalstr:
                if s[i - 1: i + 1] not in legalstr:
                    return 0
                else:
                    c = a 
            else:
                if s[i - 1: i + 1] in legalstr:
                    c = b+a
                else:
                    c = b
            a = b
            b = c # 滚动起来
        return c  

③ 动态规划（LeetCode 官方解法）

• 对于给定的字符串 s，设它的长度为 n，其中的字符从左到右依次为 s[1],s[2],⋯,s[n]，可以使用动态规划的方法计算出字符串 s 的解码方法数。
• 具体地，设 f_i 表示字符串 s 的前 i 个字符 s[1…i] 的解码方法数。在进行状态转移时，可以考虑最后一次解码使用了 s 中的哪些字符，那么会有下面的两种情况：
• • 第一种情况是使用了一个字符，即 s[i] 进行解码，那么只要 s[i] ≠ 0，它就可以被解码成 A∼I 中的某个字母。由于剩余的前 i−1 个字符的解码方法数为 f_i−1，因此我们可以写出状态转移方程：f_i = f_i−1，其中 s[i] ≠ 0；
• • 第二种情况是使用了两个字符，即 s[i−1] 和 s[i] 进行编码，与第一种情况类似，s[i−1] 不能等于0，并且 s[i−1] 和 s[i] 组成的整数必须小于等于 26，这样它们就可以被解码成 J∼Z 中的某个字母。由于剩余的前 i−2 个字符的解码方法数为 f_i−2，因此可以写出状态转移方程：f_i = f_i−2，其中 s[i−1] ≠ 0 并且 10⋅s[i−1]+s[i]≤26，需要注意的是，只有当 i>1 时才能进行转移，否则 s[i−1] 不存在。
• 将上面的两种状态转移方程在对应的条件满足时进行累加，即可得到 分 f_i 的值，在动态规划完成后，最终的答案即为 f_n。
• Python 示例：

class Solution:
    def numDecodings(self, s: str) -> int:
        n = len(s)
        f = [1] + [0] * n
        for i in range(1, n + 1):
            if s[i - 1] != '0':
                f[i] += f[i - 1]
            if i > 1 and s[i - 2] != '0' and int(s[i-2:i]) <= 26:
                f[i] += f[i - 2]
        return f[n]

• 注意到在状态转移方程中，f_i 的值仅与 f_i-1 和 f_i-2 有关，因此可以使用三个变量进行状态转移，省去数组的空间：

class Solution:
    def numDecodings(self, s: str) -> int:
        n = len(s)
        # a = f[i-2], b = f[i-1], c = f[i]
        a, b, c = 0, 1, 0
        for i in range(1, n + 1):
            c = 0
            if s[i - 1] != '0':
                c += b
            if i > 1 and s[i - 2] != '0' and int(s[i-2:i]) <= 26:
                c += a
            a, b = b, c
        return c