leetcode之动态规划刷题总结4
Posted nuist__NJUPT
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了leetcode之动态规划刷题总结4相关的知识,希望对你有一定的参考价值。
leetcode之动态规划刷题总结4
1-最长回文子序列
题目链接:题目链接戳这里!!!
思路:动态规划
dp[i][j]:表示从下标i到下标j的最大回文序列
若s[i]==s[j]
递推式如下:
dp[i][j] = dp[i+1][j-1]+2 ;
若s[i]!=s[j]
递推式如下:
dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]) ;
class Solution
public int longestPalindromeSubseq(String s)
int n = s.length() ;
int [][] dp = new int [n][n] ;
for(int i=0; i<n; i++)
dp[i][i] = 1 ;
for(int i=n-1; i>=0; i--)
for(int j=i+1; j<n; j++)
if(s.charAt(i) != s.charAt(j))
dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]) ;
else
dp[i][j] = dp[i+1][j-1]+2 ;
return dp[0][n-1] ;
2-一和零
题目链接:题目链接戳这里!!!
思路:背包问题的变形题
这道题和经典的背包问题非常相似,但是和经典的背包问题只有一种容量不同,这道题有两种容量,即选取的字符串子集中的 0 和 1的数量上限。
经典的背包问题可以使用二维动态规划求解,两个维度分别是物品和容量。这道题有两种容量,因此需要使用三维动态规划求解,三个维度分别是字符串、0 的容量和 1 的容量。
定义三维数组 dp,其中dp[i][j][k] 表示在前 i 个字符串中,使用 j 个 0 和 k 个 1 的情况下最多可以得到的字符串数量。
状态转移方程如下:
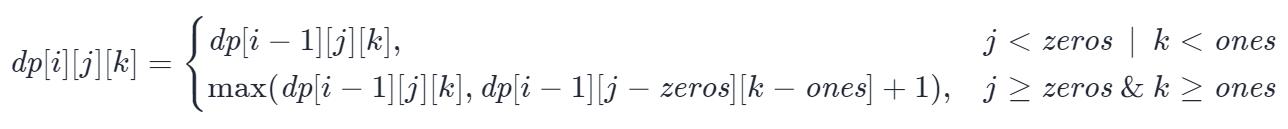
class Solution
public int findMaxForm(String[] strs, int m, int n)
int len = strs.length ;
int [][][] dp = new int [len+1][m+1][n+1] ;
for(int i=1; i<=len; i++)
int [] zero =count(strs[i-1]) ;
int zeros = zero[0], ones = zero[1] ;
for(int j=0; j<=m; j++)
for(int k=0; k<=n; k++)
if(j>=zeros && k>=ones)
dp[i][j][k] = Math.max(dp[i-1][j][k],dp[i-1][j-zeros][k-ones]+1) ;
else
dp[i][j][k] = dp[i-1][j][k] ;
return dp[len][m][n] ;
public int [] count(String s)
int [] zeros = new int [2] ;
for(int i=0; i<s.length(); i++)
zeros[s.charAt(i)-'0']++ ;
return zeros ;
3-使用最小花费爬楼梯
题目链接:题目链接戳这里!!!
思路:dp[i]:表示爬到当前i位置所需要的最小花费
dp[0]=0
dp[1]=0
递推表达式:
dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]) ;
class Solution
public int minCostClimbingStairs(int[] cost)
int [] dp = new int [cost.length+1] ;
for(int i=2; i<=cost.length; i++)
dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]) ;
return dp[cost.length];

4-零钱兑换II
题目链接:题目链接戳这里!!!
思路:用 dp[x] 表示金额之和等于 x的硬币组合数,目标是求 dp[amount]。动态规划的边界是dp[0]=1。只有当不选取任何硬币时,金额之和才为 0,因此只有 1 种硬币组合。
class Solution
public int change(int amount, int[] coins)
int [] dp = new int [amount+1] ;
dp[0] = 1 ;
for(int coin : coins)
for(int i=coin; i<=amount; i++)
dp[i] += dp[i-coin] ;
return dp[amount] ;

5-优美的排列
题目链接:题目链接戳这里!!!
思路1:dfs+标记
每轮搜索,只要当前数字和下标相互可以取余,则累加排列数,继续搜索。每次搜索需要标记已经搜索过的数字。
class Solution
public int countArrangement(int n)
return dfs(n,1,new boolean[n+1]) ;
public int dfs(int n, int i, boolean [] vis)
if(i>n)
return 1 ;
int ans = 0 ;
for(int num=1; num<=n; num++)
if(!vis[num] &&(i%num==0 || num%i==0))
vis[num] = true ;
ans += dfs(n,i+1,vis) ;
vis[num] = false ;
return ans ;
思路2:回溯法
我们可以使用回溯法解决本题,从左向右依次向目标排列中放入数即可。
具体地,我们定义函数backtrack(i,n),表示尝试向位置 i放入数。其中 n 表示排列的长度。在当前函数中,我们首先找到一个符合条件的未被使用过的数,然后递归地执行 backtrack(i+1,n),当该函数执行完毕,回溯到当前层,我们再尝试下一个符合条件的未被使用过的数即可。
回溯过程中,我们可以用vis 数组标记哪些数被使用过,每次我们选中一个数 idx,我们就将vis[idx] 标记为 true,回溯完成后,我们再将其置为false。
特别地,为了优化回溯效率,我们可以预处理每个位置的符合条件的数有哪些,用数组 match 保存。当我们尝试向位置 i 放入数时,我们只需要遍历 match[i] 即可。
class Solution
List<Integer> [] match ;
boolean [] vis ;
int num ;
public int countArrangement(int n)
match = new List[n+1] ;
vis = new boolean[n+1] ;
for(int i=1; i<=n; i++)
match[i] = new ArrayList<>() ;
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
if(i%j==0 || j%i==0)
match[i].add(j) ;
backtrack(1,n) ;
return num ;
public void backtrack(int i, int n)
if(i==n+1)
num++ ;
return ;
for(int idx : match[i])
if(!vis[idx])
vis[idx] = true ;
backtrack(i+1,n) ;
vis[idx] = false ;
6-出界的路径数
题目链接:题目链接戳这里!!!
思路:搜索+标记
每轮沿着四个方向搜索,能出界就累加1,步数为0时,不能出界,返回0,搜索完成需要标记当前位置在某一步数下已经搜索的答案,下轮搜索遇到时,直接返回即可。
class Solution
int [] dx = -1,1,0,0 ;
int [] dy = 0,0,-1,1 ;
int [][][]cache ;
int mod = 1000000007;
public int findPaths(int m, int n, int maxMove, int startRow, int startColumn)
cache = new int [m][n][maxMove+1] ;
for(int i=0; i<m; i++)
for(int j=0; j<n; j++)
for(int k=1; k<=maxMove; k++)
cache[i][j][k] = -1 ;
return dfs(startRow,startColumn,maxMove,m,n) ;
public int dfs(int x, int y, int maxMove, int m, int n)
if(x<0 || y<0 || x>=m || y>=n)
return 1 ;
if(maxMove==0)
return 0 ;
if(cache[x][y][maxMove]!=-1)
return cache[x][y][maxMove] ;
int ans = 0 ;
for(int i=0; i<4; i++)
int tx = x + dx[i] ;
int ty = y + dy[i] ;
ans += dfs(tx,ty,maxMove-1,m,n) ;
ans = ans % mod ;
cache[x][y][maxMove] = ans ;
return ans ;
思路:动态规划
动态规划的状态由移动次数、行和列决定,定义 dp[i][j][k] 表示球移动 i次之后位于坐标 (j,k) 的路径数量。
class Solution
int [] dx = -1,1,0,0 ;
int [] dy = 0,0,-1,1 ;
int mod = 1000000007 ;
public int findPaths(int m, int n, int maxMove, int startRow, int startColumn)
int [][][] dp = new int [maxMove+1][m][n] ;
dp[0][startRow][startColumn] = 1;
int sum = 0 ;
for(int i=0; i<maxMove; i++)
for(int j=0; j<m; j++)
for(int k=0; k<n; k++)
int count = dp[i][j][k] ;
if(count > 0)
for(int x=0; x<4; x++)
int tx = j + dx[x] ;
int ty = k + dy[x] ;
if(tx>=0 && tx<m && ty>=0 && ty<n)
dp[i+1][tx][ty] = (dp[i+1][tx][ty]+count) % mod ;
else
sum = (sum+count)%mod ;
return sum ;

7-两个字符串的删除操作
题目链接:题目链接戳这里!!!
思路:dp[i][j]表示以i-1的字符串word1,以j-1结尾的字符串word2要达到相等,所需删除的元素的最少个数。
若word1[i-1]等于word2[j-1]则不需要删除,递推式如下:
dp[i][j] = dp[i-1][j-1] ;
若word1[i-1]不等于word2[j-1],则需要删除,分为三种可能,递推式如下:
dp[i][j] = Math.min(dp[i-1][j]+1,Math.min(dp[i][j-1]+1,dp[i-1][j-1]+2)) ;
class Solution
public int minDistance(String word1, String word2)
int [][] dp = new int [word1.length()+1][word2.length()+1] ;
for(int i=1; i<word1.length()+1; i++)
dp[i][0] = i ;
for(int j=1; j<word2.length()+1; j++)
dp[0][j] = j ;
for(int i=1; i<word1.length()+1; i++)
for(int j=1; j<word2.length()+1; j++)
if