用Matlab软件实现变长NLMS自适应滤波器算法

Posted 2023-03-20

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了用Matlab软件实现变长NLMS自适应滤波器算法相关的知识，希望对你有一定的参考价值。

一种具有双瞬变因子的LMS自适应滤波算法

曾召华刘贵忠马社祥

（西安交通大学信息与通信工程研究所西安710049）

作者在文献〔4〕中提出了一种改进的瞬变步长SPLMS自适应滤波算法。本文在SPLMS算法的基础上，进一步提出一种基于瞬变步长、瞬变平滑因子的双瞬变SPLMS算法—DSPLMS算法。该算法除具有常规LMS算法简单的优点外，还具有更高的起始收敛速率、更小的权失调噪声和更大的抑噪能力。文中重点讨论瞬变步长、瞬变平滑因子的变化特性。计算机仿真结果支持了理论分析。
自适应滤波器，失调噪声，收敛速度，最小均方误差，瞬变因子
1 引言
自适应滤波器及其相应算法是多年来人们广泛研究的课题。基于Widrow－Hoff标准的LMS算法和其相应的自适应滤波器以其算法和结构简单，便于实时信号处理等优点，在不同领域得到了最为广泛的应用。而为克服常规的固定步长LMS或牛顿LMS（Newton LMS，即NLMS）自适应算法在收敛速率、跟踪速率与权失调噪声之间要求上存在的较大矛盾，人们发展了各种各样的改进型LMS算法，如基于瞬变步长LMS自适应滤波算法〔1～6〕、基于正交变换（DCT、FFT、小波变换、子带滤波）的新型LMS均衡算法〔7～8〕。基于模糊判断的自适应LMS系统识别和基于最小四次均方误差的LMS自适应平稳收敛算法〔9～10〕。在所有改进型LMS算法中，瞬变步长LMS自适应滤波算法是研究最为广泛的一类LMS自适应滤波算法。本文算法也是基于瞬变因子的一种改进LMS自适应滤波算法。
2 SPLMS算法分析及问题的提出
在文献〔4〕中，作者对上述方案进行了大量的计算机仿真和理论分析，结果表明：（1）上述诸种算法的收敛速率与系统输入信噪比SNR直接相关，信噪比SNR越高，它们的收敛速率普遍提高；随着信噪比SNR的降低，它们的收敛速率减慢，甚至出现发散现象，因此它们必须在弱干扰下完成规一化起动，即在起始过程中噪声要相当小，否则效果不佳。（2）在上述所有算法中，由于采用瞬时平方误差性能函数e2k来代替均方误差性能函数，所以其算法的权值收敛过程表现为加权矢量的平均值变化规律和由于噪声引起的随机起伏项的叠加。因此，噪声方差越大，则随机起伏项越大，表现为权值振动也就越大。（3）为了追求更快的收敛性，往往增大μ和M，但滤波器阶数越高，步长因子μ和输入功率越大，就便得失调系数也越大。在有限次数起动迭代过程中，也就很难收敛到较稳态值，所以必须寻求更佳的瞬态步长算法。
文献〔4〕在准最小均方（Pseudo－LMS，即PLMS）误差算法基础上通过采用滑动时间窗，减少PLMS算法起动过程的计算量；同时在权值迭代中加一平滑迭代而使PLMS算法具备全局较强的抗噪性能，较快速收敛性能而提出了SPLMS算法，即：

其中rk为M阶滤波器输入信号的功率估值；Wk为滤波器的第k步M维最优权矢量估值；Xk是滤波器输入信号的M维输入数据矢量；dk为希望输出；μk为滤波器第k步瞬态步长。切换条件中，阈值μ类似于LMS算法的步长因子μL，满足：

μL＜μ＜1／trR，R＝E〔XkXTk〕（7）

为待定的算法常数，是μk变化的动态平衡点。而α是一常数为平滑因子，它决定上一次的权值变化对本次权值更新的影响程度。k0是采用式（2）规一化启动后，算法收敛到较稳态时的步数。式（4）是μk下降的递推算法，式（5）是μk上升的平滑递推算法。λ为上升的速度因子，满足0＜λ＜1。在实际应用中，考虑到学习过程的启动速度，一般取较大的λ值，即：

0．9＜λ＜1，k0＝25～35，｜α｜＜0．3（8）

SPLMS算法的实质是：在开始k0步中，采用启动速度较快的MLMS（Mend LMS）算法收敛到相对较稳态的状态；然后在k≥k0＋1过程中，采用瞬态步长μk来训练算法。而μk根据不同的切换条件将围绕μ作升降变化，其迭代计算主要表现为不降即升的动态过程。α主要根据经验来取值，输入数据的非平稳性越大，噪声方差越大时，增大α可明显抑制振动，从而加速收敛过程；在噪声小时减小α。
但SPLMS算法也有一明显不足，即α主要根据经验来取值，没有理论上的确切依据。α取值不当，反而容易造成算法收敛性能更差，甚至发散的现象。从理论上分析，α与瞬态步长μk和输出误差ek（文中定义为：ek＝dk－WTk Xk）应有一定关系。在算法启动阶段，ek较大，为追求启动速度而常取较大步长μk，但μk越大，权失调系数也就越大，有时反而起不到应有的作用，这时就应相应增加α值来平滑权失调噪声；在算法渐趋稳定，步长μk渐趋于常数，ek渐趋于0，此时α也应渐趋于0。综合起来就是：α应随步长μk和误差ek瞬时变化而变化，也应是一瞬变因子。本文重点就是寻求瞬变因子αk的数学表达式以满足上述分析的要求。
3 改进的双瞬变因子SPLMS算法——DSPLMS算法
3．1 μk的变化特性
从式（4）和式（5）可以看出，在k≥k0＋1过程中，μk根据不同的切换条件将围绕μ作升降变化，μk的迭代计算主要表现为不降即升的动态过程。对于式（5），设k≥kr时，μk＜μ，则在k≥kr＞k0＋1的上升过程中：

即上升速度按指数衰减，使趋于平衡点μ的上升速度迅速减小。其变化过程类似于一电阻电容串联电路上电容的充电过程。对式（4），由于μk＝μk－1／（1＋Rk），Rk＞0，即使很小的Rk经过一步迭代就足以使μk＜μ，再次切换到上升过程。当rk较大时，下降形成的负脉冲也较大。
综上所述，在k≥k0＋1的收敛过程中，μk的时变特性等价于幅值极不对称的随机正负尖脉冲序列组成的瞬态分量和直流分量μ的线性叠加。瞬态分量的负脉冲强度与rk瞬值对应，有利于抑制局部自激或短暂发散，减小权矢量噪声，提高稳定度。在rk较小、算法渐趋于稳定时，瞬变分量趋于0，μk～μ。
3．2 αk的变化特性
定义：ΔWk＝Wk＋1－Wk为自适应滤波器的权系数增量；ξ为均方误差性能函数，ξ＝E〔ek〕2，ek＝dk－WTk Xk为输出误差，则SPLMS算法的权系数更新公式由式（1）可重写为：

Wk＋1＝Wk－μk＾Wξk＋αΔWk－1（10）

其中Wξ为ξ的梯度函数，＾W为Wξ的第k步估计。由式（10）的系数更新公式，我们可写出均方误差性能函数的表达式：

式中上标T表示矢量的转置。若用一矢量＾Wζk＋1去左乘式（10），则可得到：
＾Wξk＋1Wk＋1＝＾Wζk＋1Wk－μk＾Wζk＋1＾Wζk＋＾Wζk＋1αΔWk－1（13）

利用式（12）的结论，可将式（13）化简为：

＾TWζk＋1ΔWk＝0（14）

由于参量μk和α均为实的标量因子，故式（14）又可写成：

（μk＾TWζk＋1）（αΔWk）＝0（15）

式（15）清楚地表明：在SPLMS算法中，自适应滤波器的权系数在迭代过程中，其均方误差性能函数的梯度估值与权系数增量始终存在一个正交关系。ΔWk－1对ΔWk的调节作用是在当前梯度估值方向上，给出与梯度估值方向正交矢量，并以这两个矢量所构成的合矢量来改变权系数空间的权重。
对于FIR结构的LMS自适应系统而言，其均方误差性能函数在平稳输入时为一个二次型函数，在收敛点附近仍可视为一个二次型函数，故有：

ξ（Wk＋1）＝WTk RWk－2WTk P＋C（16）

式中R＝E〔XTk Xk〕为输入信号的自相关矩阵，P＝E〔dkXk〕为所需信号与输入信号的互相关矢量，C＝E〔d2k〕，则由式（16）可得：

将式（17）代入式（18），则式（18）可变形为：

式（19）就是本文给出的瞬变平滑因子αk的数学表达式。显然，它满足前面分析时所提出的要求，且在算法达到稳态收敛时，满足：

limk→∞αk＝0（20）

3．3 改进的双瞬变SPLMS算法——DSPLMS算法
用式（19）中αk的表达式替换式（1）中的α，就得到本文提出的具有双瞬变因子的LMS算法——DSPLMS算法，即
Wk＋1＝Wk＋2μk（dk－WTk Xk）Xk＋αk（Wk－Wk－1）（21）

μk＝λ／（1＋2λrk），0≤k≤k0（22）

由式（19）、（20）可知，αk是一个与μk成正比且具有衰减性的瞬变因子，从而使本文提出的DSPLMS算法比SPLMS算法更能快速稳定收敛；与常规LMS算法相比，其性能有极大的提高，为实时信号处理提供了一个较好的算法。
4 计算机仿真
仿真实验的结构如图1所示，其中dk为随机输入信号，nk为高斯白噪声，ek为输出误差，xk为自适应滤波器的输入，yk为滤波器输出，此时xk＝dk＋nk。

在图2中，dk是均值为0、方差为1的高斯白噪声；nk是与dk不相关的均值为0、方差为1的高斯白噪声；滤波器参数：M＝32，λ＝0．9，μL＝0．005，μ＝0．01，α＝0．1。在图3中，nk为均值为0、方差为0．1的高斯白噪声，其它参数同图2。图2、3为分别采用LMS、SPLMS和DSPLMS算法进行滤波的学习曲线比较图。

从图2（强干扰启动）和图3（较弱干扰启动）中可以看出：在强干扰下，DSPL MS 具有比SPLMS好、比LMS好得多的启动速度和收敛速度；而在弱干扰下，DSPLMS仍具有比SPLMS快、比LMS快得多的启动速度。从图中同时还可看出：DSPLMS与SPLM S具有几乎相同的收敛速度，它们的收敛速度比LMS快得多。
5 结语
加进瞬变平滑项的规一化起动，使DSPLMS具有更高的起始收敛速度、更小的权失调噪声和更大的抑噪能力；在平稳连接之后的稳态过程中，该算法趋于步长为μ的LMS算法性能，但由于瞬变分量负脉冲的作用，在相近的权失调量下可按式（7）取较大的μ值，增强算法对时变参数过程的跟踪处理能力；输入数据的非平稳性越大，噪声方差越大时，加进的瞬变平滑项使权失调噪声减小，从而使本文提出的DSPLMS算法比SPLMS算法更能快速稳定地收敛；与常规LMS算法相比，其性能有极大的提高，可以明显抑制振动，从而加速收敛过程。

网址：
追问

这不是我要的NLMS算法啊，毕业导师要求必须是NLMS算法，别的他不采纳的，还有没有更贴近的答案啊

参考技术A clear all
close all
N=10; %滤波器阶数
sample_N=500; %采样点数

A=1; %信号幅度
snr=10; %信噪比
t=1:sample_N;
length_t=100; %期望信号序列长度
d=A*sin(2*pi*t/length_t); %期望信号
M=length(d); %M为接收数据长度
x=awgn(d,snr); %经过信道（加噪声）

delta=1/(10*N*(A^2)); %计算能够使LMS算法收敛的delta

y=zeros(1,M);
h=zeros(1,N); %LMS滤波器系数
h_normalized=zeros(1,N); %归一化LMS滤波器系数
y1=zeros(1,N);
for n=N:M %系数调整LMS算法
x1=x(n:-1:n-N+1);
%LMS算法
y(n)=h*x1';
e(n)=d(n)-y(n);
h=h+delta*e(n)*x1;
%NLMS算法
y_normalized(n)=h_normalized*x1';
e_normalized(n)=d(n)-y_normalized(n);
h_normalized=h_normalized+e_normalized(n)*x1/(x1*x1');
end
error=e.^2; %LMS算法每一步迭代的均方误差
error_normalized=e_normalized.^2; %NLMS算法每一步迭代的均方误差
for n=N:M %利用求解得到的h，与输入信号x做卷积，得到滤波后结果
x2=x(n:-1:n-N+1);
y1(n)=h*x2';
y2(n)=h_normalized*x2';
end
subplot(411)
plot(t,d);
axis([1,sample_N,-2,2]);
subplot(412)
plot(t,x);
subplot(413)
plot(t,y);
subplot(414)
plot(t,y_normalized);
figure(2)
plot(t,error,'r',t,error_normalized,'b');本回答被提问者采纳

信号检测基于matlab自适应滤波法微弱信号检测含Matlab源码 2308期

⛄一、自适应滤波法微弱信号检测

1 NLMS自适应滤波
1.1 NLMS自适应滤波基本原理
最小均方 (LMS) 误差自适应滤波器[4]是将输入信号x (t) 通过系数可调的加权滤波器后, 与期望的参考信号d (t) 比较, 得到误差信号e (t) 。采用特定的滤波算法调节滤波器权系数w (t) , 最终使误差信号的均方差E[e2 (t) ]达到最小值, 滤波器的输出更接近期望参考信号, 达到最优滤波。由LMS可以推出滤波器权系数的递推公式为

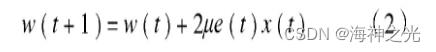
归一化LMS (NLMS) 算法[5,6,7]是一种变步长的LMS算法, 比LMS算法具有更快的收敛速度。它在滤波的初始阶段, 步长较大, 收敛速度较快;当算法收敛后, 减小步长μ, 以保证较高的收敛精度。由NLMS可推出滤波权系数递推公式为

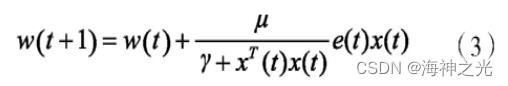
式中, γ是为了避免xT (t) x (t) 过小而设定的参数, 通常情况下的取值范围为0≤γ≤1。

1.2 原始信号的预处理
由自适应滤波的基本原理可知, NLMS自适应滤波器的实现需要已知输入信号的期望信号作为参考信号。但环境声音去噪处理中, 很难预先已知目标声音谱信息来构建参考信号, 因此常规的自适应滤波器很难满足要求。由于目标信号并非白噪声, 而是由液体的振动产生, 有一定的振动规律。因此本文采用一种以自身原始信号作为滤波的期望信号, 使其既为原始信号也为期望信号的方法, 进行自适应滤波。滤波后的误差时域图如图2所示。

从图2中可以看出, 在误差时域中, 目标信号之前的干扰信号被削弱, 而目标信号却得以加强, 起到了抑制干扰、突出目标特征的作用。滤波后以误差信号的时域幅值代替原始信号的时域幅值进行下一步的特征分析。

3 端点检测
端点检测的目的就是在复杂的应用环境下的信号流中分辨出干扰信号和目标信号, 并确定目标信号的开始及结束。主要通过短时能量及瞬时过零率对目标信号进行检测, 当出现的信号满足目标信号的各项特征, 则其被认为是目标信号, 即目标信号的开始端。

3.1 检测识别基本流程
检测识别目标信号时, 同时对滤波后的信号进行短时能量及瞬时平均过零率的判别。当被检测信号均超过两者的门限后, 才被认定为疑似信号。对于疑似信号, 将继续进行时间门限的判别, 只有其超过能量及过零率门限的时间均大于已设定的时间门限, 才被认为是目标信号 (图3) 。

3.2 短时能量门限
首先用短时能量进行判别, 并设定一个高门限, 当信号能量超过此门限后, 进行下一步持续时间门限判断。检测时, 要对声音信号进行加窗分帧处理, 如果窗的长度过大, 在提高检测速度的同时导致识别率的下降;如果窗的长度过短, 在提高检测识别率的同时增加了检测的时间。因此, 采用动态窗长短时能量端点检测方法, 在检测到疑似目标信号时使用大窗长, 出现疑似目标信号后, 改用小窗长。将短时能量[8,9,10]定义为

图3 基本流程图

图4 (a) 为信号在时域内幅度的变化情况, 第5 s处附近有误导噪声, 第12 s处目标信号音 (油爆裂声) 开始出现, 这两处波形呈现明显的尖锐增大。图4 (b) 为能量随时间推移的变化情况, 虽采用帧数计数, 但其时间进度与图4 (a) 的时间进度完全对应。

根据图4考虑设置过渡段的时间门限, 算法在检验到有疑似目标信号时开始计时, 若信号短时能量值没能在设定的时间门限范围内持续, 则认为其为无效信号;若超过时间门限, 则认为信号有效。利用这一能量特性可以实现对信号的辨识, 辨识的精确度高于传统的幅度辨识。但仅凭这个特征判断目标信号还不可靠, 还需要对疑似信号作进一步的识别与确认。

3.3 瞬时平均过零率门限
过零是指信号波形穿越时间轴或零值线, 对于离散时间信号而言, 就是相邻的取样值符号改变。平均过零率即为单位时间 (或单位样本) 内过零的次数[11,12]。计算一个声音信号帧内单位时间越过零线的平均次数, 可以得出其瞬时平均过零率或瞬时平均过零数。当信号瞬时平均过零率超过此门限后, 进行下一步持续时间门限判断。瞬时平均过零率的计算方法可表示为

图5 (a) 为信号在时域内幅度的变化情况, 第5 s处附近有误导噪声, 第12 s处目标信号音 (油爆裂声) 开始出现, 这两处波形呈现明显的尖锐增大。图5 (b) 为信号的瞬时过零率统计, 虽采用帧数计数, 但其时间进度与图5 (a) 的时间进度完全对应。

同样设置时间门限与过零率门限, 通过短时能量判别的信号, 可进一步进行过零率判别。若信号没能在设定的时间门限范围内持续, 则认为其为无效信号;若超过时间门限, 则认为信号有效。

⛄二、部分源代码

% RANDOM PROCESS_NOISE MODULE
clear all
close all
n=100000;
fs=n;
t=0:1/fs:(fs-1)/fs;
yss=1sin(2pi1000t);
% 高斯色噪声
x1=normrnd(0,3,1,n);
p=0.5;
f0=0.05;
a1=-2pcos(2pif0);
a2=p^2;
x2=zeros(1,n);
for i=3:1:n;
x2(i)=a1x2(i-1)-a2x2(i-2)+x1(i);
end
%散粒噪声
lamda=2;Tmax=10000;
i=1;T(1)=random(‘exponential’,lamda);
while(T(i)<Tmax)
T(i+1)=T(i)+random(‘exponential’,lamda);
i=i+1;
end
T(i)=Tmax;x=0:1:i;w(1)=0;
for p=1:i
w(p+1)=T§;
end
%length(w)
%length(x)
figure(1)
stairs(w,x)
ylabel(‘事件发生次数’);
xlabel(‘事件发生时间’);
title(‘泊松过程（lamda=2，Tmax=50）’);
fs=100000;
t=(1/fs:1/fs:1)Tmax;
a=0.1;
W=fs/Tmaxw;
W=floor(W);
n3=zeros(length(W)-1,fs);
for k1=2:1:length(W);
k=W(k1);
tn=1:1:fs;
yp=exp(-(tn-k)*a);
for kp=1:1:k-1
yp(kp)=0;
end
n3(k1-1,:)=yp;
end