蚁群算法 解决 0-1背包问题

Posted 2022-02-18 软件工程小施同学

                  蚁群算法实现0-1背包问题实验报告

【实验内容】

用蚁群算法求解0-1背包问题。

【实验环境】

Microsoft Visual C++ 6.0

【基本理论】

       蚁群算法是对自然界蚂蚁的觅食寻径方式进行模似而得出的一种仿生算法。先简要介绍一下蚂蚁搜寻食物的具体过程。研究表明：蚁群在觅食途中，会在所经过路径留下一种挥发性分泌物—信息素(pheromone) ，并能感知其存在和强度，朝着信息素浓度高的方向移动。与此同时释放出与路径长度有关的信息素。路径越长，释放的激索浓度越低。浓度越高的路径选择它的蚂蚁越多，越发增加该路径上的信息素浓度，这样又吸引更多的蚂蚁，从而形成一个正反馈。蚂蚁最终总能找到一条从食物到巢穴之间的最优路径。最优路径上的激索浓度越来越大。而其它路径上的激素浓度却会随着时间的流逝而消减。最终整个蚁群会找出觅食最优路径。

用人工蚂蚁来模仿自然蚂蚁，在走过的路径上留下信息素，为解决各种寻优问题提供了一种新的方法。该算法已经被成功地应用在很多复杂的组合优化问题上。Dorigo 首先将该方法用于求解TSP 问题，随后很多学者陆续使用了该算法解二次分配问题、皇后问题等。所解决的问题以TSP 问题为主，另外有函数优化问题、背包问题等，而且从离散空间扩展到了连续空间。在解决这些问题的性能方面，比之于传统的优化算法，蚂蚁优化算法表现出了良好的性能。

#include "iostream"
#include <fstream>
#include <string>
#include <time.h>

using namespace std;

#define M 8//蚂蚁数
#define P 0.2//信息素挥发率
#define MAX 70
int BRoute[MAX];//最优解
int BValue=0;//最优解的总价值
int BWeight;//最优解的总重量
int max_circle=500;//外循环最大次数
int antRoute[9][MAX];
int antValue[9];
void main()
	int n;//物品个数
	int w_limit;//背包重量限制
	int value[MAX];//各物品价值
	int weight[MAX];//各物品重量
    float inf[MAX][MAX];//信息素矩阵
	int i,j;



	// ************** 读数据 *************************//
	string filestring;
	cout<<"请输入测试文件名: ";
	cin>>filestring;
	
	ifstream inFile(filestring.c_str());
	//报告错误
	if(!inFile)
	
		cerr<<"不能打开测试文件："<<filestring<<endl;
		exit(-1);
	
    
	inFile>>n;
	inFile>>w_limit;

	value[0]=0;
    weight[0]=0;
	for (i=1; i<=n; i++)
	
		inFile >> weight[i];  
		
	for (i=1; i<=n; i++)
	
		inFile >> value[i]; 

	

	//************************* 信息素矩阵初始化 ********************//
	
	for(i=0;i<=n;i++)
		inf[i][0]=0;
	for(i=0;i<=n;i++)
		for(j=1;j<=n;j++)
			inf[i][j]=1;
		
	
	

	//************************ 数据输出 ****************************//
	cout<<"物品总数为："<<n<<endl;
	cout<<"背包重量限制为："<<w_limit<<endl;

	cout<<"各物品重量分别为："<<endl;
   	for(i=0;i<=n;i++)
		cout<< weight[i]<<" ";
	cout<<endl<<endl;

	cout<<"各物品价值分别为："<<endl;
    for(i=0;i<=n;i++)
		cout<< value[i]<<" ";
	cout<<endl<<endl;

	srand((int)time(0)); //初始化随机种子
	bool mark[MAX];
	int no_modify=0;
	for(int k=1;k<=max_circle && no_modify<100 ;k++)//外循环
//	for(int k=1;k<=max_circle  ;k++)//外循环
		for(i=1;i<=M;i++)
			antRoute[i][0]=0;
			int Cur_n=0; //已选取物品个数
			int Cur_w=0; //已选取物品总重量
			int Cur_v=0; //已选取物品总价值
			int Cur_ps=0; //记录当前选取物品的标号
		    for(j=1;j<=n;j++)
				mark[j]=false; //作为物品是否选取的标志
			bool finish=false; 
		   	int ok[MAX]; 
			while(finish==false)
				if(Cur_n==n)
					antRoute[i][++Cur_n]=0;
					antValue[i]=Cur_v;
					finish=true;
					
				
				else
					int ok_n=0;
					for(j=1;j<=n;j++)
						if(mark[j]==false &&(Cur_w+weight[j])<=w_limit)
							ok[ok_n++]=j; //该数组用于存储满足条件的物品的标号
						
					
					if(ok_n==0) //无满足条件的物品
						antRoute[i][++Cur_n]=0;
						antValue[i]=Cur_v;
						finish=true;
					
					else
						//有满足条件的物品：按信息素来进行随机选取
						float total=0;
						float rate[MAX];						
					
						for(j=0;j<ok_n;j++)
							float total=total+inf[Cur_ps][ok[j]];							
						
						for(j=0;j<ok_n;j++)
							rate[j]=(inf[Cur_ps][ok[j]]/total);
							
						bool choose=false;
						while(choose==false)
							double r=(double)(rand() % 1001) * 0.001f;
							int u=(int)(rand()%ok_n);
							if(rate[u]>r)
									antRoute[i][++Cur_n]=ok[u];
									Cur_ps=ok[u];
									Cur_w+=weight[ok[u]];
									Cur_v+=value[ok[u]];
									mark[ok[u]]=true;
									choose=true;
									break;		
							

							/*
                            for(j=0;j<ok_n;j++)
								if(leiji[j]>r)
									antRoute[i][++Cur_n]=ok[j];
									Cur_ps=ok[j];
									Cur_w+=weight[ok[j]];
									Cur_v+=value[ok[j]];
									mark[ok[j]]=true;
						//			cout<<endl<<"选中"<<ok[j]<<endl;
									choose=true;
									break;		
							*/

						
				
					//else

				//else
			//while

		//for:内循环
        
		//与当前最优解比较
		int temp=0;
		for(i=1;i<=M;i++)
			if(antValue[i]>BValue)
				BValue=antValue[i];
				temp=i;
			
		
		if(temp==0)
			no_modify++; //记录连续不改变的次数，达到一定值时停止外循环
		if(temp!=0)
			no_modify=0;
			for(int s=0;s<MAX;s++)
				BRoute[s]=antRoute[temp][s];
			
		
		
	//信息素更新/
	//挥发
		for(i=0;i<=n;i++)
			for(j=0;j<=n;j++)
				inf[i][j]*=(1-P);
			
	//最优解再进行信息素的增强
        inf[BRoute[0]][BRoute[1]]+=P/n;
		for(int s=1; s<MAX && BRoute[s]!=0;s++)
			inf[BRoute[s]][BRoute[s+1]]+=P/n;			
		

	//外循环
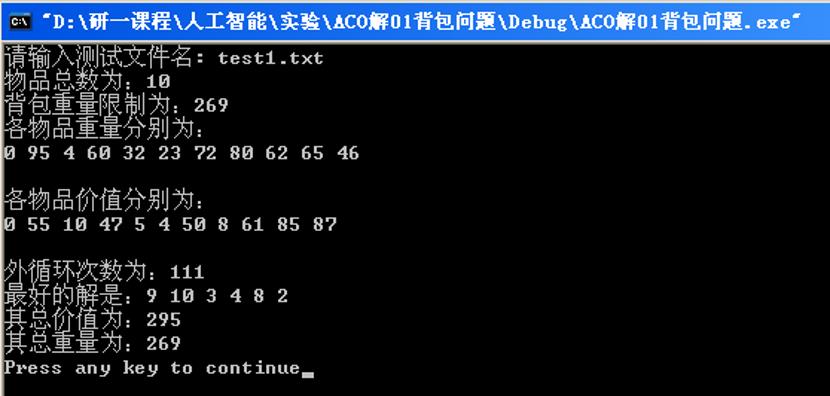
	cout<<"外循环次数为："<<k<<endl;
	cout<<"最好的解是：";
	for( k=1;k<MAX && BRoute[k]!=0;k++)
		cout<<BRoute[k]<<" " ;
	cout<<endl<<"其总价值为："<<BValue<<endl;
	BWeight=0;
	for(int s=1;s<MAX && BRoute[s]!=0;s++)
		BWeight=BWeight+weight[BRoute[s]];

	cout<<"其总重量为："<<BWeight<<endl;

ACO（蚁群算法）解01背包问题_ACO算法解决背包问题-其它文档类资源-CSDN下载