matlab基于普通DE实现基本自适应差分进化算法(SaDE)
Posted 唐人街小白
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了matlab基于普通DE实现基本自适应差分进化算法(SaDE)相关的知识,希望对你有一定的参考价值。
提出背景
由于给定所求的函数条件下,我们无法准确知道求解该函数适于怎样取值的变异算子F和交叉概率CR,由此推出自适应差分进化算法(DE)。
2.实现方法
为了使所用的F与CR尽量符合所求函数的要求,我们设定一个初始的交叉概率最大值CEm,初始值设为0.5,并生成服从正态分布且取值在(0.3,0.5)区间的随机数F。设定一个自适应取值的节点LP,即在迭代次数为LP是进行自适应值的改变。为了结合各个变异策略的优点,我们再次选用同CoDE类似的方法,即选取多个变异策略进行迭代,改变自适应度的同时对选取的几种变异策略的选用概率进行自适应改变。
以下为我们选取的四种变异策略

3.代码实现
close all;
clear all;
clc;
%--------------------初始化各参数值------------------------------------------------------
NP=100;
CRm=0.5;
G=100;
LP=10;
D=2;
a=-5;
b=5;
Aa=1;
A=[];
ikun1=0.25;
ikun2=0.25;
ikun3=0.25;
ikun4=0.25;
c=0;
t=0;
r=0;
l=0;
C=0;
T=0;
R=0;
L=0;
x=rand(NP,D)*(b-a)+a; %随机生成初始种群
v=zeros(NP,D);
u=zeros(NP,D);
minx=9999;
best=0;
for i=1:NP %求各个个体的适应度并取出适应度最好的个体的位置
fit(i)=4*x(i,1)^2-2.1*x(i,1)^4+1/3*x(i,1)^6+x(i,1)*x(i,2)-4*x(i,2)^2+4*x(i,2)^4;
if fit(i)<minx
minx=fit(i)
best=i;
end
end
trace(1)=minx;
for g=1:G %开始迭代
num=randsrc(1,1,[1 2 3 4;ikun1 ikun2 ikun3 ikun4]); %对选取的策略按照相应概率进行选取
F=normrnd(0,0.33333)*0.1+0.4; %生成符合正态分布的F值
CR=normrnd(0,0.33333)*((CRm-0.1)/2)+((CRm+0.1)/2); %生成符合正态分布的CR值
%--------------------变异操作----------------------------------------------------------------
for m=1:NP
num1=randperm(NP,1);
if num1==m
num1=randperm(NP,1);
end
num2=randperm(NP,1);
if (num2==m)||(num2==num1)
num2=randperm(NP,1);
end
num3=randperm(NP,1);
if (num3==m)||(num3==num1)||(num3==num2)
num3=randperm(NP,1);
end
num4=randperm(NP,1);
if (num4==m)||(num4==num1)||(num4==num2)||(num4==num3)
num4=randperm(NP,1);
end
num5=randperm(NP,1);
if (num5==m)||(num5==num1)||(num5==num2)||(num5==num3)||(num5==num4)
num5=randperm(NP,1);
end
if num==1
C=C+1;
for i=1:NP
v(i,:)=x(num1,:)+F*(x(num2,:)-x(num3,:));
end
end
if num==2
T=T+1;
for i=1:NP
v(i,:)=x(best,:)+F*(x(num1,:)-x(num2,:))+F*(x(num3,:)-x(num4,:));
end
end
if num==3
R=R+1;
for i=1:NP
v(i,:)=x(num1,:)+F*(x(num2,:)-x(num3,:))+F*(x(num4,:)-x(num5,:));
end
end
if num==4
L=L+1;
for i=1:NP
v(i,:)=x(i,:)+F*(x(best,:)-x(i,:))+F*(x(num1,:)-x(num2,:));
end
end
end
%--------------------交叉操作--------------------------------------------------------
for n=1:1:D
cr=rand;
if(cr<=CR)||(n==r)
u(:,n)=v(:,n);
else
u(:,n)=x(:,n);
end
end
%--------------------修补染色体--------------------------------------------------------
for m=1:1:NP
for n=1:1:D
if u(m,n)<=a
u(m,n)=a;
end
if u(m,n)>=b
u(m,n)=b;
end
end
end
%--------------------重新求适应度,优胜劣汰----------------------
for i=1:NP
fit1(i)=4*u(i,1)^2-2.1*u(i,1)^4+1/3*u(i,1)^6+u(i,1)*u(i,2)-4*u(i,2)^2+4*u(i,2)^4;
if fit1(i)<minx
x(i,:)=u(i,:);
A(1,Aa)=CR;
Aa=Aa+1;
minx=fit1(i);
best=i;
end
end
trace(g+1)=minx;
%--------------------对CR进行自适应取值----------------------
if g==LP
CRm=mean(A(:)); %求所有发生进化的个体所选用的CR的平均值
Aa=1;
clear A; %清空重置A矩阵
A=[];
%--------------------根据所选策略与其成功概率决定以后该策略的选取概率----------------------
if num==1
c=c+1;
end
if num==2
t=t+1;
end
if num==3
r=r+1;
end
if num==4
l=l+1;
end
if C~=0&&c~=0
ikunn1=c/C;
else
ikunn1=0;
end
if T~=0&&t~=0
ikunn2=t/T;
else
ikunn2=0;
end
if R~=0&&r~=0
ikunn3=r/R;
else
ikunn3=0;
end
if L~=0&&l~=0
ikunn4=l/L;
else
ikunn4=0;
end
if ~(c==0&&t==0&&r==0&&l==0)
ikun1=ikunn1/(ikunn1+ikunn2+ikunn3+ikunn4);
ikun2=ikunn2/(ikunn1+ikunn2+ikunn3+ikunn4);
ikun3=ikunn3/(ikunn1+ikunn2+ikunn3+ikunn4);
ikun4=ikunn4/(ikunn1+ikunn2+ikunn3+ikunn4);
end
end
end
%--------------------结束迭代,绘制迭代次数与适应度的关系图----------------------
x(1,:);
figure(1);
title(['差分进化算法(DE)','最小值','num2str(tt)']);
xlabel('迭代次数');
ylabel('目标函数值');
plot(trace);
4.运行结果
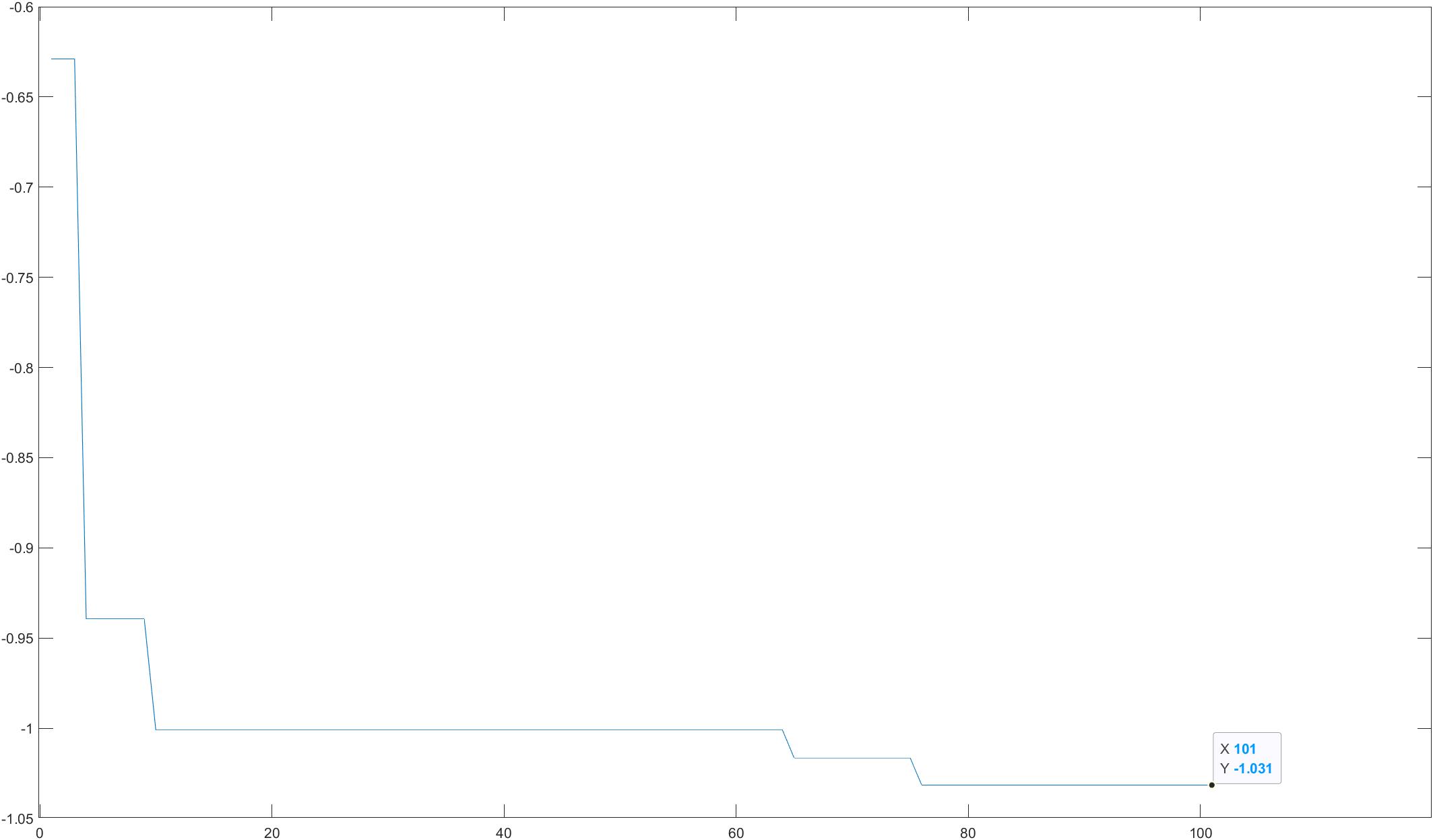
差分进化算法求解函数最优解matlab实现
一、简介
差分进化算法(Differential Evolution,DE)由Storn和Price于1995年首次提出。主要用于求解实数优化问题。该算法是一类基于群体的自适应全局优化算法,属于演化算法的一种,由于其具有结构简单、容易实现、收敛快速、鲁棒性强等特点,因而被广泛应用在数据挖掘、模式识别、数字滤波器设计、人工神经网络、电磁学等各个领域。1996年在日本名古屋举行的第一届国际演化计算(ICEO)竞赛中,差分进化算法被证明是速度最快的进化算法。
和遗传算法一样,差分进化算法也是一种基于现代智能理论的优化算法,通过群体内个体之间的相互合作与竞争产生的群体智能来指导优化搜索的方向。该算法的基本思想是:从一个随机产生的初始种群开始,通过把种群中任意两个个体的向量差与第三个个体求和来产生新个体,然后将新个体与当代种群中相应的个体相比较,如果新个体的适应度优于当前个体的适应度,则在下一代中就用新个体取代旧个体,否则仍保存旧个体。通过不断地进化,保留优良个体,淘汰劣质个体,引导搜索向最优解逼近。
为了使更多研究者了解和研究差分进化算法,Storn和Price于1997年建立了差分进化算法的官方网站,该网站的建立得到了广大研究者的关注和支持,为相关人员进行差分演化算法的理论和应用研究提供了极大的方便。此外,Store和Price在差分进化算法上没有申请任何形式的专利,这也为推动差分进化算法的研究和应用起到了重要的作用。
二、步骤:
其具体进化流程如下:
(1)确定差分进化算法控制参数,确定适应度函数。差分进化算法控制参数包括:种群大小NP、缩放因子F与杂交概率CR。
(2)随机产生初始种群。
(3)对初始种群进行评价,即计算初始种群中每个个体的适应度值。
(4)判断是否达到终止条件或进化代数达到最大。若是,则终止进化,将得到最佳个体作为最优解输出;若否,继续。
(5)进行变异和交叉操作,得到中间种群。
(6)在原种群和中间种群中选择个体,得到新一代种群。
(7)进化代数g=g+1,转步骤(4)
三、运行结果

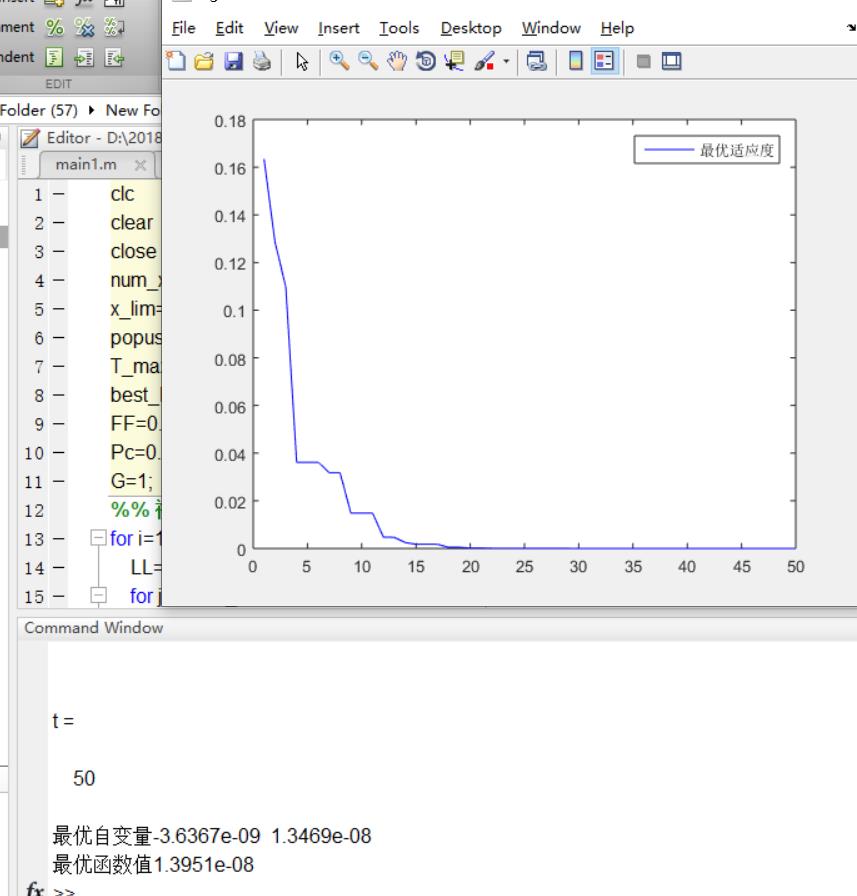
四、代码
https://download.csdn.net/download/weixin_41971010/20386308
原理可以参照这篇文章:
https://blog.csdn.net/qq_37423198/article/details/77856744
以上是关于matlab基于普通DE实现基本自适应差分进化算法(SaDE)的主要内容,如果未能解决你的问题,请参考以下文章