线性卷积、周期卷积、圆周卷积的异同

Posted 2023-03-20

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了线性卷积、周期卷积、圆周卷积的异同相关的知识，希望对你有一定的参考价值。

一、三者的计算不同：

1、线性卷积的计算：线性卷积的计算可以用解析法，也可以用图解法。若两个序列的长度分别为N1和N2，则卷积结果的总长度应为L=N1+N2-1。

同理，对线性非时变连续系统来说，若连续时间信号x(t)是系统的输入，h(t)是系统在单位脉冲作用下的单位冲激响应，则系统在零状态的输出为它们的卷积积分。

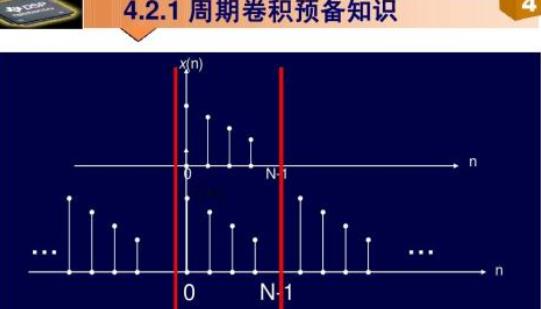
2、周期卷积的计算：周期长度均为N的两个周期序列y(n)和:xz (n)进行如下形式的运算:乙x gym)za (n一m)称为周期卷积。通常记为:x1 (n )④iz <n )。周期卷积的结果仍然是以N为周期的序列。

3、圆周卷积的计算：离散信号的圆周卷积可以经由圆周卷积定理使用快速傅立叶变换（FFT）而有效率的计算。因此，若原本的（线性）卷积能转换成圆周卷积来计算，会远比直接计算更快速。

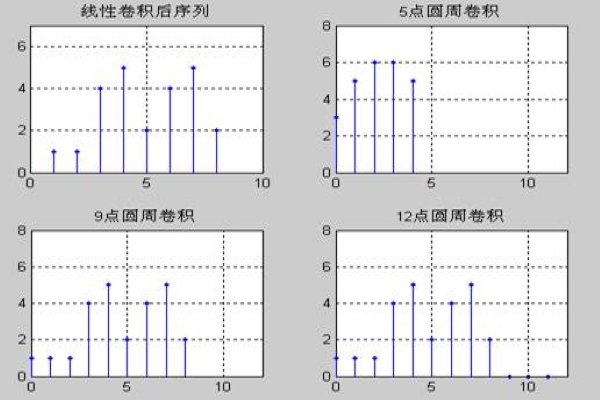
二、三者性质不同：

1、线性卷积的性质：符合结合律、交换律、分配律。

2、周期卷积的性质：仅符合交换率。

3、圆周卷积的性质：符合交换律、分配律。

三、三者的实质不同：

1、线性卷积的实质：线性卷积在时域描述线性系统输入和输出之间关系的一种运算。这种运算在线性系统分析和信号处理中应用很多，通常简称卷积。

2、周期卷积的实质：周期卷积是一种数学运算方法。

3、圆周卷积的实质：两个函数的圆周卷积是由他们的周期延伸所来定义的。周期延伸意思是把原本的函数平移某个周期T的整数倍后再全部加起来，所产生的新函数。

参考资料来源：百度百科-线性卷积

参考资料来源：百度百科-周期卷积

参考资料来源：百度百科-圆周卷积

参考技术A

1、对于线性非时变离散时间系统来说，若序列x(n)是系统的输入，h(n)是系统在单位脉冲作用下的单位脉冲响应，则由于输入序列x(n)可表示为一系列脉冲的线性组合，所以，根据线性系统的叠加性质，系统的输出在系统初始不储能的条件下(零状态响应)可由图1式求得。

2、周期卷积是一种数学运算方法，运算符合交换律。

3、周期长度均为N的两个周期序列y(n)和:xz (n)进行如下形式的运算:乙x gym)·.za (n一m)称为周期卷积.通常记为:x1 (n )④iz <n ).周期卷积的结果仍然是以N为周期的序列，其运算符合交换律。

两个函数的圆周卷积是由他们的周期延伸所来定义的。周期延伸意思是把原本的函数平移某个周期 T 的整数倍后再全部加起来，所产生的新函数。

扩展资料

周卷积可以经由圆周卷积定理使用快速傅立叶变换（FFT）而有效率的计算。因此，若原本的（线性）卷积能转换成圆周卷积来计算，会远比直接计算更快速。考虑到长度L 和长度 M 的有限长度离散信号，做卷积之后会成为长度

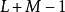
的信号，因此只要把两离散信号补上适当数目的零（zero-padding）成为 N 点信号，其中

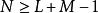
，则它们的圆周卷积就与卷积相等。即可接着用 N 点 FFT 作计算。

参考资料来源

百度百科-线性卷积

百度百科-圆周卷积

百度百科-周期卷积

参考技术B 线性卷积就是多项式系数乘法：设a的长度是M，b的长度是N，则a卷积b的长度是M+N-1，运算参见多项式乘法。
“L点的圆周卷积”就是把先做线性卷积，再把结果的前L点保留不动，后面的点截下来，加到结果的头上去。如果L>M+N-1，则线性卷积和圆周卷积相同。
没听说过周期卷积，是不是圆周卷积的另一种说法？本回答被提问者采纳参考技术C 线性卷积适用于有限长序列，上楼的已经说清楚了
周期卷积，顾名思义，只适用于周期序列。可以这样来思考，因为周期序列是无限长的序列，如果采用线性卷积的那套方法，即无限长序列的卷积，那么，周期卷积的值必定为无穷大。因而这是没有意义的。随意，周期卷积只取从0到N-1区间值的加和，从而也可推得周期卷积后的序列也必定为周期序列。
圆周卷积适用于有限长序列。先把两个点数都是N的序列周期延拓，进行周期卷积和后再去主值序列。圆周卷积后的序列是有限长序列。参考技术D 楼上说法正确。但有周期卷积。圆周卷积是周期卷积的主值序列，即周期卷积的结果是圆周卷积结果的周期延拓。