第26篇MobileNets：用于移动视觉应用的高效卷积神经网络

Posted 2022-02-12 AI浩

MobileNets：用于移动视觉应用的高效卷积神经网络

摘要

我们提出了一类称为 MobileNets 的高效模型，用于移动和嵌入式视觉应用。 MobileNets 基于流线型架构，使用深度可分离卷积来构建轻量级深度神经网络。 我们引入了两个简单的全局超参数，可以有效地在延迟和准确性之间进行权衡。 这些超参数允许模型构建者根据问题的约束为其应用程序选择合适大小的模型。 我们在资源和准确性权衡方面进行了广泛的实验，并与 ImageNet 分类上的其他流行模型相比表现出强大的性能。 然后，我们展示了 MobileNets 在广泛的应用和用例中的有效性，包括对象检测、细粒度分类、人脸属性和大规模地理定位。

一、简介

自从 AlexNet [19] 通过赢得 ImageNet Challenge: ILSVRC 2012 [24] 普及了深度卷积神经网络以来，卷积神经网络在计算机视觉中变得无处不在。 总体趋势是制作更深、更复杂的网络以实现更高的准确度[27,31,29,8]。 然而，这些提高准确性的进步并不一定会使网络在规模和速度方面更有效率。 在机器人、自动驾驶汽车和增强现实等许多现实世界应用中，识别任务需要在计算能力有限的平台上及时执行。

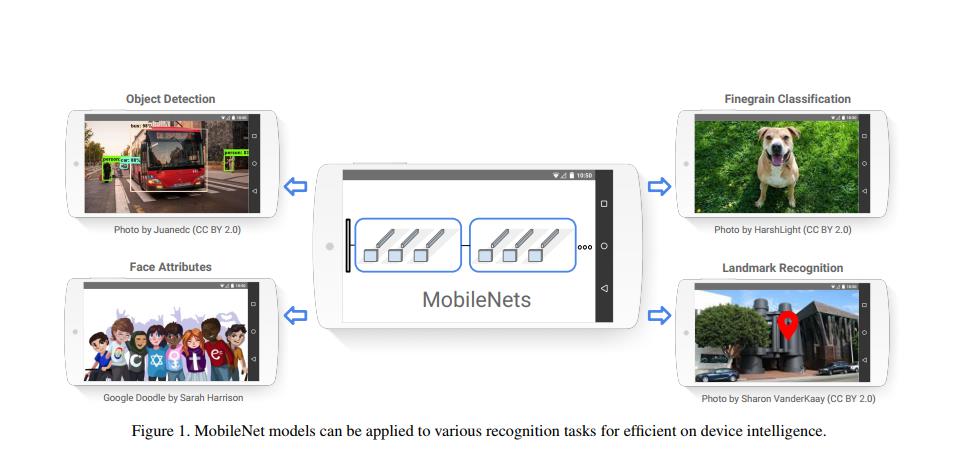
本文描述了一种高效的网络架构和一组两个超参数，以构建非常小的、低延迟的模型，可以轻松地满足移动和嵌入式视觉应用的设计要求。 第 2 节回顾了构建小型模型的先前工作。 第 3 节描述了 MobileNet 架构和两个超参数宽度乘数和分辨率乘数，以定义更小、更高效的 MobileNet。 第 4 节描述了 ImageNet 上的实验以及各种不同的应用程序和用例。 第 5 节以总结和结论结束。

二、前期工作

在最近的文献中，人们对构建小型高效神经网络的兴趣日益浓厚，例如[16, 34,12, 36, 22]。许多不同的方法通常可以分为压缩预训练网络或直接训练小型网络。本文提出了一类网络架构，允许模型开发人员专门选择一个与其应用程序的资源限制（延迟、大小）相匹配的小型网络。

MobileNets 主要专注于优化延迟，但也产生小型网络。许多关于小型网络的论文只关注规模而不考虑速度。 MobileNets 主要由最初在 [26] 中引入的深度可分离卷积构建，随后用于 Inception 模型 [13] 以减少前几层的计算。 Flattened networks [16] 用完全分解的卷积构建了一个网络，并展示了极度分解网络的潜力。与当前的论文无关，Factorized Networks[34] 引入了类似的分解卷积以及拓扑连接的使用。随后，Xception 网络 [3] 演示了如何扩展深度可分离滤波器以超越 Inception V3 网络。另一个小型网络是 Squeezenet [12]，它使用瓶颈方法来设计一个非常小的网络。其他简化计算网络包括结构化变换网络 [28] 和油炸卷积网络 [37]。

获得小型网络的另一种方法是缩小、分解或压缩预训练网络。 文献中提出了基于乘积量化[36]、散列[2]和剪枝、矢量量化和霍夫曼编码[5]的压缩。 此外，已经提出了各种分解来加速预训练网络 [14, 20]。 训练小型网络的另一种方法是蒸馏 [9]，它使用较大的网络来训练较小的网络。 它是我们方法的补充，并在第 4 节中的一些用例中进行了介绍。另一种新兴方法是低比特网络 [4,22,11]。

三、MobileNet 架构

在本节中，我们首先描述构建 MobileNet 的核心层，这些核心层是深度可分离过滤器。然后我们描述了 MobileNet 网络结构，最后描述了两个模型收缩超参数宽度乘数和分辨率乘数。

3.1、深度可分离卷积

MobileNet 模型基于深度可分离卷积，这是一种分解卷积的形式，它将标准卷积分解为深度卷积和称为点卷积的 1×1 卷积。对于 MobileNets，深度卷积将单个过滤器应用于每个输入通道。然后逐点卷积应用 1×1 卷积来组合深度卷积的输出。标准卷积在一个步骤中既可以过滤输入，也可以将输入组合成一组新的输出。深度可分离卷积将其分为两层，一个用于过滤的单独层和一个用于组合的单独层。这种分解具有显着减少计算量和模型大小的效果。图 2 显示了如何将标准卷积 2(a) 分解为深度卷积 2(b) 和 1 × 1 点卷积 2©。

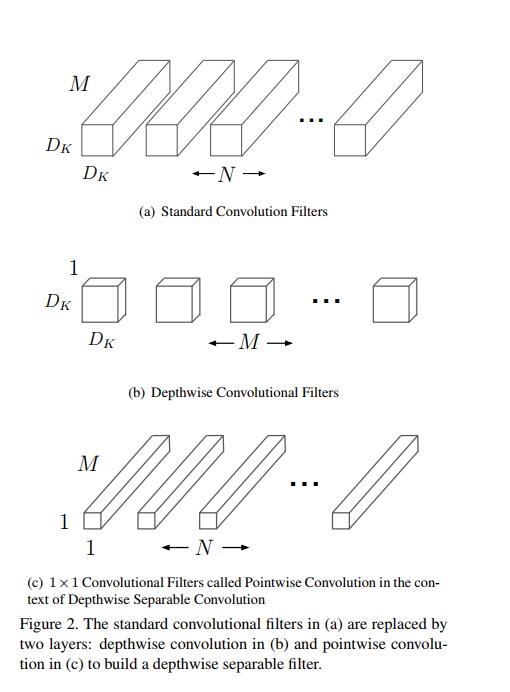
标准卷积层将 $D_F\times D_F\times M$ 特征图 F 作为输入，并生成 $D_F\times D_F\times N$ 特征图 G，其中 $D_F$ 是正方形输入特征图 1 的空间宽度和高度，M 是输入通道数（ 输入深度），$D_G$ 是正方形输出特征图的空间宽度和高度，N 是输出通道数（输出深度）。

标准卷积层由大小为 $D_K\times D_K\times M\times N$的卷积核 K ，其中 $D_K$ 是假设为正方形的内核的空间维度，M 是输入通道数，N 是前面定义的输出通道数 。

假设步幅为 1 和填充的标准卷积的输出特征图计算如下：
$${\mathbf{G}}_{k,l,n}=\sum _{i,j,m}{\mathbf{K}}_{i,j,m,n}\cdot {\mathbf{F}}_{k+i-1,l+j-1,m}\text{\hspace{1em}(1)}$$
标准卷积的计算成本为：
$$D_K\cdot D_K\cdot M\cdot N\cdot D_F\cdot D_F\text{\hspace{1em}(2)}$$
其中计算成本乘法地取决于输入通道的数量 M、输出通道的数量 N、内核大小 $D_k\times D_k$和特征图大小 $D_F\times D_F$。 MobileNet 模型解决了这些术语及其相互作用。 首先，它使用深度可分离卷积来打破输出通道数和内核大小之间的相互作用。

标准卷积操作具有基于卷积核过滤特征并组合特征以产生新表示的效果。 过滤和组合步骤可以通过使用称为深度可分离卷积的分解卷积分为两个步骤，以显着降低计算成本。

深度可分离卷积由两层组成：深度卷积和点卷积。 我们使用深度卷积为每个输入通道（输入深度）应用一个过滤器。 点卷积，一个简单的 1×1 卷积，然后用于创建深度层输出的线性组合。 MobileNets 对两个层都使用了 batchnorm 和 ReLU 非线性。

每个输入通道（输入深度）一个滤波器的深度卷积可以写成：
$${\hat{\mathbf{G}}}_{k,l,m}=\sum _{i,j}{\hat{\mathbf{K}}}_{i,j,m}\cdot {\mathbf{F}}_{k+i-1,l+j-1,m}\text{\hspace{1em}(3)}$$

其中$\hat{\mathbf{K}}$是大小为 $D_K\times D_K\times M$ 的深度卷积核，其中 $\hat{\mathbf{K}}$中的第 m 个滤波器应用于 F 中的第 $m_{th}$ 个通道，以生成过滤后的输出特征图$\hat{\mathbf{G}}$的第 m 个通道。

深度卷积的计算成本为：
$$D_K\cdot D_K\cdot M\cdot D_F\cdot D_F\text{\hspace{1em}(4)}$$
相对于标准卷积，深度卷积非常有效。 然而，它只过滤输入通道，并没有组合它们来创建新功能。 因此，需要一个额外的层，通过 1 × 1 卷积计算深度卷积输出的线性组合，以生成这些新特征。

深度卷积和 1×1（逐点）卷积的组合称为深度可分离卷积，最初是在 [26] 中引入的。

深度可分离卷积计算成本：
$$D_K\cdot D_K\cdot M\cdot D_F\cdot D_F+M\cdot N\cdot D_F\cdot D_F\text{\hspace{1em}(5)}$$
这是depthwise和1×1 pointwise卷积的总和。

通过将卷积表示为过滤和组合的两步过程，我们可以减少以下计算：
D K ⋅ D K ⋅ M ⋅ D F ⋅ D F + M ⋅ N ⋅ D F ⋅ D F D K ⋅ D K ⋅ M ⋅ N ⋅ D F ⋅ D