Java版高级数据结构堆树&堆排序

Posted 2022-02-11 chenry777

本文涉及代码实现github地址: https://github.com/chenruoyu0319/data-structure-for-java/tree/main/%E5%A0%86%E6%A0%91

一、堆树

堆是什么？堆是一种特殊的树，他需要满足以下两点：

1.是一颗完全二叉树

2.其每一个节点的值都大于等于或者小于等于其左右子节点的值。

• 补充：完全二叉树：除了最后一层，其他层每个节点都是满的且最后一层的节点都要靠左排列。

大顶堆：首元素为堆内最大的元素

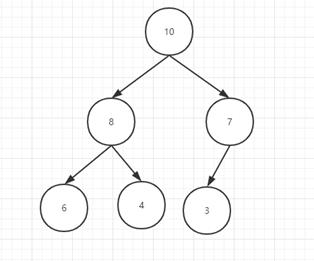
小顶堆：首元素为堆内最小的元素

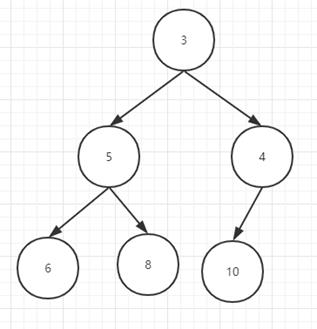
二、堆树的存储

堆树是一棵完全二叉树，所以堆的存储结构和完全二叉树的最佳存储结构相同，就是用数组来存储。因为它有着特殊的属性，直接利用下标就可以表示左右节点。

左节点：2*i , 右：2*i + 1，其中 i 就是我们当前点所在数组的下标。

如果下标从0开始开始 ，这两个公式则变成：2*i+1和2*i+2

三、堆树的插入和删除

1.插入

堆的插入过程就叫做堆化，我们只需要在堆的末尾，也就是放到数组的最后一个元素的下一个元素空间中，然后把这个新插入的数"自下而上"做循环交换来满足堆树的性质，直到依次往上做到不能交换为止，如下图，我们新插入了一个元素9，维护一个大顶堆：

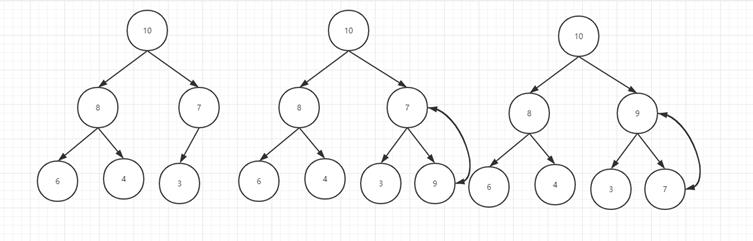
这个过程的时间复杂度也很好计算，就是在当前节点和它的2个子节点中取最大的值做一个比较，也就是底数为3的log(n/2)。

2.删除

堆顶的删除操作，我们只需要把堆顶元素和堆尾元素做一个交换，然后删除堆尾元素，再对堆顶元素自上而下做一次堆化即可。

思考：这里为啥不能直接删除，然后用左右节点代替呢？ 因为这样会造成我们的树不是一颗完全二叉树，因为会少点。

3.注意事项

无论是自上而下堆化，还是自下而上堆化，都涉及到元素值的交换，故一定要注意在交换后，要继续满足其子树的堆化性质。

三、堆排序

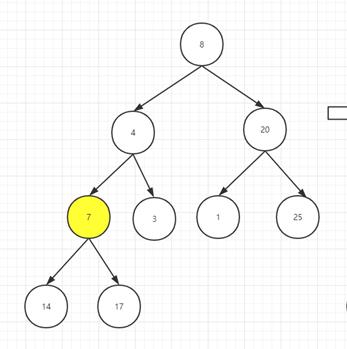
假设给你一个序列：8 4 20 7 3 1 25 14 17，如何利用堆树进行排序呢？

• 1.存储：先按照序列顺序存储在完全二叉树中。

• 2.建堆：从最后一个非叶子节点自下而上进行堆化。

• 3.交换：交换堆头和堆尾元素，再自上而下进行循环的堆化，其中已经交换完的堆尾元素不变。

这么说比较抽象，具体可以看博主的github代码，每一步都有详细的注释，也有展示了具体的堆排序每一步数据变化的过程。

四、堆应用

1.用来实现优先级队列

2.用来解决TOP K问题，比如给你一串1000万的数字，求前k大的数。

一种是静态的数据

一种是动态的的数据

3.用来实现定时任务

比如，可以用来解决如下算法问题：给你1亿个不重复的数字（整数，1~2^32-1），求出top10。前10大的数字，还可动态添加新数字，但总个数不会超过1亿。

决如下算法问题：给你1亿个不重复的数字（整数，1~2^32-1），求出top10。前10大的数字，还可动态添加新数字，但总个数不会超过1亿。

具体代码在博主的github中已经实现，可供参考。