ShuffleNetv2论文译读笔记

Posted 2022-02-10 songyuc

Ma, Ningning, et al. “Shufflenet v2: Practical guidelines for efficient cnn architecture design.” Proceedings of the European conference on computer vision (ECCV). 2018.

摘要

目前，神经网络的架构设计大多时有非直接的计算复杂度指标来引导的，例如：FLOPs。然而，对于速度这样的直接指标则还需要取决于其它的因素，例如：内存访问开销和平台特性。因此，本文提出在目标平台上进行评价的直接指标，比仅仅考虑FLOPs更好。基于一系列实验，本文总结出多个用于高校网络设计的指导原则。相应地，提出一种新的网络架构，称之为ShuffleNetv2。验证性的消融实验证明提出的模型在速度和精度的均衡性上达到了SOTA。

1 引言

  CNN的架构在多年的发展中，变得更加准确和快速。自从AlexNet【1_AlexNet】里程碑式的出现，ImageNet分类准确率在新型架构上获得了巨大提升，其中包括VGG【2_VGG】、GoogLeNet【3_GoogLeNet】、ResNet【4_ResNet, 5_Identity_Mappings】、DenseNet【6_DenseNet】、ResNeXt【7_ResNeXt】和SE-Net【8_SE-Net】，以及自动神经架构搜索（NAS）【9_NASNET, 10_Liu2018ProgressiveNAS, 11_Real2019RegularizedNAS】等模型。
  除了准确率，计算复杂度也是另一个重要的考量。现实任务常常旨在给定计算预算下获得最佳的精度，即给定目标平台（例如：硬件设备）和应用场景（例如：自动驾驶要求低时延）。这种目标激发了一系列致力于轻量级架构以及更好的速度-精度均衡性，包括Xception【12_Xception】、MobileNet【13_MobileNet】、MobileNetv2【14_MobileNetv2】、ShuffleNet【15_ShuffleNet】和CondenseNet【16_CondenseNet】等模型。分组卷积和Depth-Wise-Convolution在这些工作中都表现的十分重要。
  为了衡量计算复杂度，一个广泛使用的指标是浮点运算次数，即FLOPs。然而，FLOPs是一种非直接的指标，是对直接指标例如速度和时延的近似，且并不是等价的，而直接指标才是真正需要关心的。这样的差异性已经在之前的工作【17_2017LearningECNN, 18_2016LearningSS, 14_MobileNetv2, 19_2017ChannelPruning】中被注意到了。例如：MobileNetv2【14_MobileNetv2】是一种比NASNET-A【9_NASNET】快很多的网络，但是它们的FLOPs相当。图1©(d)进一步地说明了这种现象，展示出FLOPs相似的网络具有不同的速度。

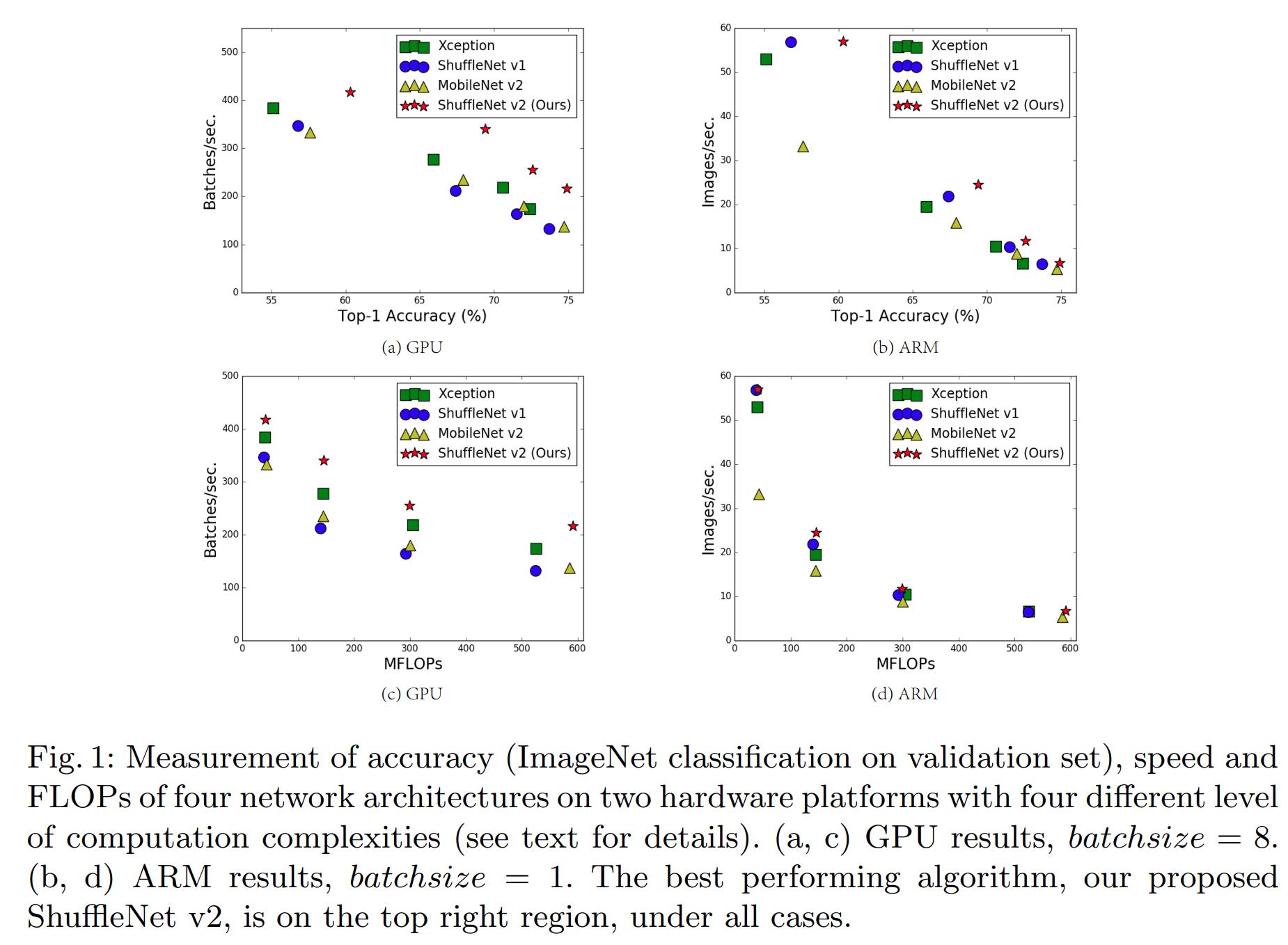
因此，使用FLOPs作为计算复杂度的唯一指标是不足的，并且会导致次优的设计。
  间接指标（FLOPs）和直接指标（速度）之间的差异来源于两个主要原因。第一，FLOPs未能考虑到几种对速度影响极大的因素。一种因素就是内存访问开销（memory access cost, MAC）。这种开销在某些操作上会占用大块的运行时间，例如Group-Convolution。它也会成为高功率设备的瓶颈，例如GPU。这种开销不应当在网络架构设计中被简单地忽略。另一种因素是并行度。在FLOPs相同的情况下，一个具有高并行度的模型会比另一个低并行度模型要快很多。
  其次，FLOPs相同的操作可能会有不同的运行时间，这取决于运算平台。举例来说，在早期工作中张量分解【20_2014SpeedingConv, 21_2015EfficientApproximations, 22_Zhang2016AcceleratingCNN】被广泛使用来加速矩阵乘法。然而，近期的文献发现【22_Zhang2016AcceleratingCNN】中的张量分解甚至在GPU上更慢，尽管它减少了75%的FLOPs。作者调研了这个问题并发现这是由于最新的CUDNN库【23_cuDNN】已经为$3\times 3$卷积进行了特别优化。作者无法肯定地认为$3\times 3$卷积比$1\times 1$卷积的计算慢9倍。
  有了这些观察发现，作者提出两项设计高效网络的原则。第一，直接指标（如：速度）应当被用于替代间接指标（如：FLOPs）。第二，这种指标需要在目标平台上评价。
  在本文中，作者遵循了这两项原则提出一种更加高效的网络架构。在第2章中作者首先分析了两种代表性SOTA网络【15_ShuffleNet, 14_MobileNetv2】的计算性能。然后，作者推想了思想高效网络设计的准则。尽管这些准则是无关平台的，作者进行了一系列控制性实验在GPU和ARM上验证了这些准则，并且进行了专门的代码优化，确保得出的结论是最新的。
  在第3章中，通过上述准则，作者设计了一种新的网络架构。由于受到ShuffleNet【15_ShuffleNet】的启发，此网络称为ShuffleNetv2。理解性验证实验证实ShuffleNetv2证实比之前的网络模型在两种平台上都更快更准，第4章图1(a)(b)中给出了总体的对照数据。

举例来说，在计算复杂性预算为40M-FLOPS的情况下，ShuffleNetv2比ShuffleNetv1和MobileNetv2的准确率高3.5%和3.7%。
【16_CondenseNet】

2 高效网络设计的实用准则

本文的研究在两个广泛使用的硬件上展开，使用了产业级优化的CNN库。作者注意到使用的CNN库比多数开源的库更加高效。因此，作者确信实验的观察和结论对产业实践是可靠且关键的。

• GPU。NVIDIA-GeForce-GTX-1080Ti单张显卡。卷积库是cuDNN-7.0【23_cuDNN】。作者还激活了cuDNN的基准测试功能来分别为不同卷积选择最快的算法。
• ARM。高通骁龙810处理器。作者使用了高效优化的基于Neon库的实现。在评测时使用单线程。

  其它设置包括：开启所有的优化选项（例如：张量融合，用于减少小型操作的负载）。输入图像大小为$224\times 224$。每个网络都进行了随机初始化并将测试100次。运行时间取平均数。
  在开始研究时，作者分析了两个SOTA网络的运行时性能，即：ShuffleNetv1【15_ShuffleNetv1】和MobileNetv2【14_MobileNetv2】。它们都是非常高效并且在ImageNet分类任务上精度很高。它们都是可以在边缘设备如手机上广泛使用。尽管作者仅分析了这两种网络，他们也注意到它们代表了当前的趋势。正如它们的核心是group-convolution和depth-wise-convolution，这些也是其它SOTA网络的关键组件，如：ResNeXt【7_ResNeXt】、Xception【12_Xception】、MobileNet【13_MobileNet】和CondenseNet【16_CondenseNet】。
  整体运行时间被分解成几个不同的操作，如图2所示。

作者注意到FLOPs指标仅考虑了卷积部分。尽管这部分需要消耗大部分实践，包括数据IO、数据Shuffle和元素级操作（AddTensor和ReLU等）的其它操作也占据了相当多的时间。因此，FLOPs不足以来准确地来衡量实际运行时间。
  基于这个发现，作者从不同方面进行了具体的运行时间（或速度）分析并推论出一些高效网络架构设计的使用准则。
  G1）相同通道宽度可最小化MAC（memory access cost）。最新的网络经常会使用深度可分离卷积（depthwise separable convolutions）【12_Xception， 13_MobileNet, 15_ShuffleNet， 14_MobileNetv2】，其中按点卷积（例如，$1\times 1$卷积）占据了大部分的复杂度【15_ShuffleNet】。作者研究了$1\times 1$卷积的卷积核形状。其形状是有两个参数指定的：输入通道数$c_1$和输出通道数$c_2$。设$h$和$w$为特征图的空间大小，则$1\times 1$卷积的FLOPs为$B=hw{c}_1{c}_2$。
  为了简化，文章认为在计算设备中的缓存空间足以存储整个特征图和参数。因此，MAC (memory access cost)或者说内存访问操作数为，$\text{MAC}=hw(c_1+c_2)+c_1{c}_2$。注意，这里的$c_1,c_2$分别对应输入/输出特征图和kernel权重的内存访问操作。
  由均值不等式可知，则有
$$\text{MAC}\ge 2\sqrt{hwB}+\frac{B}{hw}$$
  因此，MAC的下界由FLOPs给出。当输入输出的通道数相等时会达到下界。
  这项结论是理论性的。实际上，许多设备的cache（缓存）不是足够大的。此外，现今的计算库通常采用复杂的阻塞策略来充分利用缓存机制【24_DistributedDL2016】。因此，实际的MAC可能会偏离理论值。为了验证上述结论，文章进行了一项如下的实验：通过重复堆叠 10 个构建的blocks来构成一个基准网络；每个block包含两个卷积层；第一个卷积层包含$c_1$个输入通道和$c_2$个输出通道，第二个卷积层的通道数则相反（input: $c_2$, output: $c_1$）。
  表格1显示了在不同$c_1:c_2$比例而固定整体FLOPs条件下的运行速度。

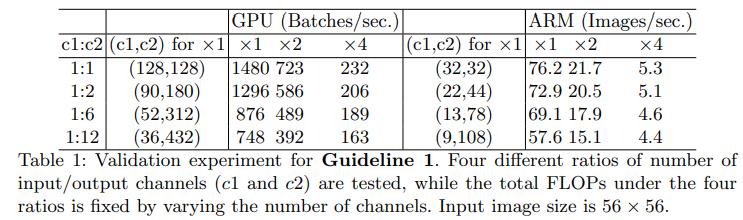
可以清楚地看到，当$c_1:c_2$接近于$1:1$时，其MAC变小而网络推理速度加快。
  G2）过度的组卷积会增加 MAC（Memory Access Cost）。Group convolution是现今网络架构【7_ResNeXt, 15_ShuffleNet, 25_DeepRoots, 26_IGCNet, 27_IGCV2, 28_IGCV3】的核心组件。它将通道间的密集卷积变成稀疏卷积（仅在通道组内卷积），从而减少了计算复杂度（FLOPs）。首先，它可以在固定FLOPs下使用更多的通道数，而提升网络容量（从而提升准确性）。另一方面，不过，增加的通道数会导致更多的MAC（Memory Access Cost）。
  遵照G1和Eq.1中的符号，$1\times 1$组卷积MAC与FLOPs间的关系为
$$\begin{array}{rl}\text{MAC}& =hw\left(c_1+c_2\right)+\frac{c_1+c_2}{g}\\ & =hw{c}_1+\frac{Bg}{c_1}+\frac{B}{hw}\end{array}$$
其中，$g$为分组数量，$B=hw{c}_1{c}_2$为FLOPs。可以看到，在给定输入形状$c_1\times h\times w$和计算成本$B$时，MAC会随着$g$增长而变大。
  为了探究以上准则的实际影响，本文构建了一项基准网络，该网络由10个 pointwise group convolution layers堆叠而成。表2展示了在固定FLOPs总数下不同组数的运行速度。

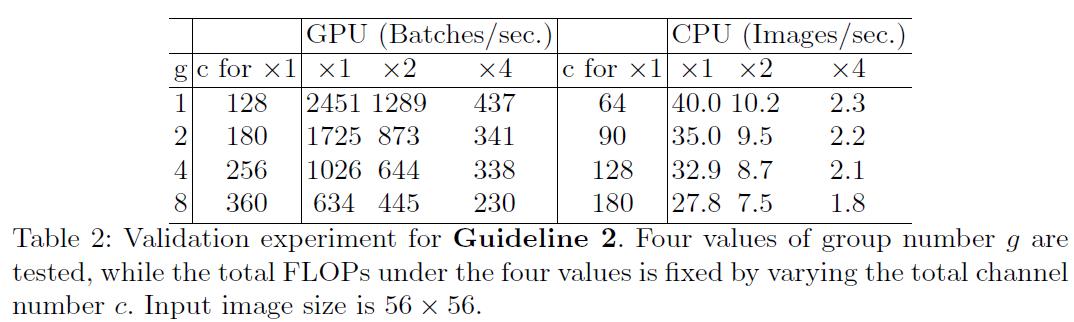
可以看到，使用大的组数会严重降低运行速度。举例来说，使用8个groups会比使用1个group（标准dense卷积）在GPU上慢两倍、在ARM上速度降低多达30%。这主要是由于MAC变多了。本文注意到这里的代码实现已经经过特别的优化，并且比单纯一组一组计算卷积要快上许多。
  因此，作者建议：组数应当根据目标平台和任务来具体调整。通用的方法是使用大的组数，从而可以用更多的通道，因为精度提升的收益很容易被计算成本的显著上升抵消。
  G3）网络分块会降低并行程度。在GoogLeNet系列【29_Residual_Connections, 30_Rethink_Inception, 3_GoogLeNet, 31_BN】和自动生成架构【9_NASNET, 11_Real2019RegularizedNAS, 10_Liu2018ProgressiveNAS】，一种“多分支”结构白广泛用于上述每个网络block中。许多微型算子（这里统称为“碎片算子”）被用于替换多个大型算子。例如，在NASNET-A【9_NASNET】中碎片算子的数量（如在一个building-block中单个卷积或池化操作的数量）为13。相对而言，在像ResNet【4_ResNet】这样的经典结构中，碎片算子数为2或3。
  尽管碎片化结构已经显示出对精度是有益的，但它仍然会降低效率，因为他对GPU 等具有强并行计算能力的设备不友好。它还引入了额外的开销，例如：kernel启动和同步。
  为了量化网络碎片化如何影响效率，本文在不同程度碎片化情况下评测了一系列网络块。具体来说，每个构建块由1到4个$1\times 1$卷积构成，以顺序或并行排列。其块结构在附录中说明。每个块重复10次。表3中结果显示了碎片化会降低GPU上的速度，例如：4-fragment结构比1-fragment结构慢3倍。在ARM上，速度降低则相对较小。
  G4）Element-wise操作的影响不可忽略。如图2所示，

在像【15_ShuffleNet， 14_MobileNetv2】轻量级模型中，element-wise操作占用了大量时间，尤其是在GPU上。这里的element-wise操作包括ReLU、AddTensor和AddBias等。它们的FLOPs较小但MAC较大。具体来说，本文也将 depthwise convolution当作element-wise算子，因其也有很高的MAC/FLOPs比。
  为进行验证，本文用ResNet【4_ResNet】中的“bottleneck”单元（$1\times 1$卷积接$3\times 3$卷积接 1 × 1 1\\times1 1×以上是关于ShuffleNetv2论文译读笔记的主要内容，如果未能解决你的问题，请参考以下文章

CBNetV2论文的译读笔记

CBNetV2论文的译读笔记

PicoDet论文译读笔记

MobileNetv3论文译读笔记

KaimingInit论文的译读笔记

魔改YOLOv5-6.x（上）结合轻量化网络Shufflenetv2Mobilenetv3和Ghostnet