生成对抗网络发展研究综述

Posted 2022-02-10 卓晴

• 姓名: 梁宇学号:2021214395
• 姓名: 牛志远学号:2021214394

 

§00 摘  要

  生成对抗网络在过去几年里得到了广泛的研究，在很多方面都取得了巨大的进步。统计学习中最重要的挑战即是如何生成大规模数据分布的样本，如图像和语音，生成对抗网络正是解决这一问题的有效方法。 GAN提供了一种无需广泛标记的训练数据来学习数据表征的方法，这种方法不需要对概率密度函数进行精确建模。

  在 GAN中，生成模型通过一个竞争过程来生成样本，生成器学习生成可信数据，判别器学习区分生成的假数据和真实数据样本，生成器和判别器同时进行训练，最后生成与训练数据同分布的生成数据。本文在介绍 GAN的主要概念和理论后，对近年来 GAN的变种做了详细的分类和讨论，并对 GAN的评价指标进行说明，对 GAN的应用进行了介绍，最后总结 GAN将来所面临的挑战和未来发展方向。

• 关键词：生成对抗网络，生成样本，博弈过程

 

§01 引  言

---

  机器学习算法大致分为两大类 -有监督学习和无监督学习。监督学习需要一个每个数据都进行标注并有各种特征的数据集，主要用于分类和回归问题。无监督学习需要一个具有多个相似标签的数据集，常用于密度估计、聚类、噪声生成和消除。

  在监督学习中，手动标记数据昂贵且耗时，自动收集数据困难且复杂。深度学习中常通过数据扩充方法提高模型效果，减少泛化误差。然而这种简单的方法仅可以获得信息有限的数据，而生成对抗网络 (Generative Adversarial Networks,GAN)[1]能够生成高质量的样本，大幅提高数据的丰富度。生成模型通常基于马尔科夫链、最大似然估计 (MLE)、近似推理和玻尔兹曼机及其开发的模型 [2]，其余的有深度置信网络 [3]以及深度波尔茨曼机 [4]。Ian Goodfellow在半监督和无监督学习的研究思路下提出了 GAN，受到了广泛的关注。

  GAN目前已经在计算机视觉、信号处理、图像合成和编辑、自然语言处理等领域取得了广泛的应用[5]。GAN的主要理论来源于零和游戏，其中一名参与者的得分正好等于另一名参与者的失分，参与者的总收益减去总损失将为 0。GAN架构由两个一起训练的网络组成:即生成器和判别器。生成器学习真实数据的数据分布，以生成能够拟合真实数据的伪数据，从而误导判别器将其视为真实输入。判别器则是一个分类器，用于区分给定输入是否来自真实数据集。两个网络不断优化以提高各自的能力，并试图从自己的弱点中学习到彼此的弱点，最终在训练中都变得更强。通过 scopu文献检索软件分析可得图1-1，图1-1展示了截止到 2020年 GAN在各学科领域应用的文章总数。

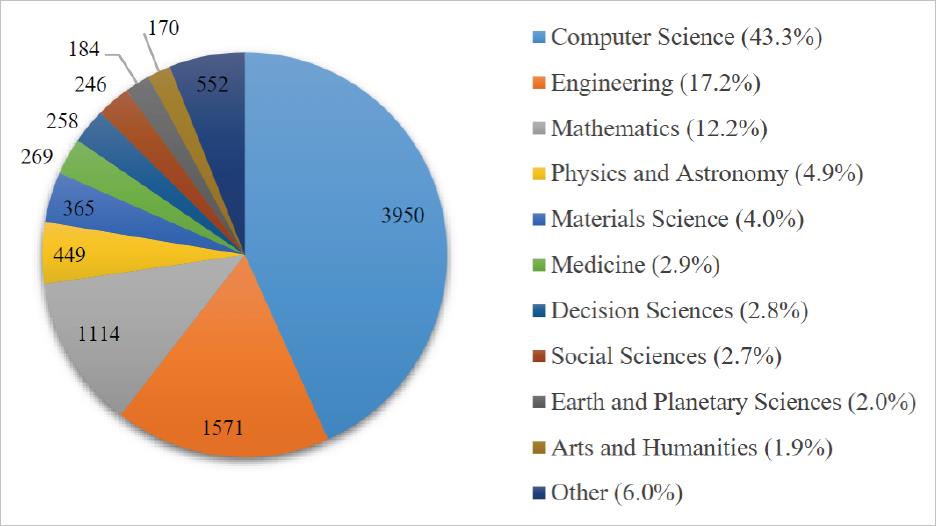
▲ 图1.1 2020年 GAN在各学科领域发表文献数

  鉴于 GAN在各个学科领域中的应用，因此有必要对其进行介绍，调查 GAN在各领域的研究近况。本文第二节将详细描述 GAN的概念和理论推导，第三节综述近年来 GAN的新架构，第四节介绍 GAN在各领域内的应用，第五节对全文进行总结。

 

§02 概念和原理

---

2.1 GAN的原理

  自从 GAN在 2014年被提出以来，这项工作就受到了广泛的关注，并且基于 GAN的新思想、新技术和新应用的有爆炸性增长。 GAN的目标是解决以下问题 :假设有一组对象数据集， GAN可以通过噪声生成相似的对象，原理是神经网络通过使用训练数据集对网络参数进行适当调整，并且深度神经网络可以用来近似任何函数。

  对于 GAN判别器函数 D和生成函数 G建模为神经网络， GAN的具体模型如图 21所示， GAN实际上包含了两个网络，一个是生成网络 G用于生成假样本，另一个是判别网络 D用于判别样本真假，并且引入对抗损失，通过对抗训练的方式让生成器生成高质量的样本。

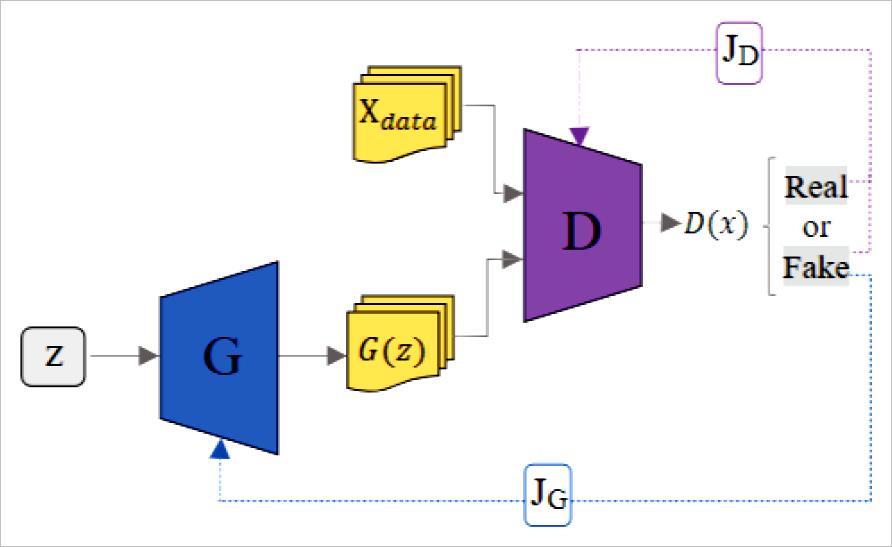
▲ 图2.1.1 GAN模型的基本结构

  对抗学习可以通过判别函数 $D\left(x\right):R^n\to \left[0,1\right]$ 和生成函数 $G:R^d\to R^n$ 之间的目标函数极大极小值实现。生成器 $G$ 将来自于 $\gamma$ 分布随机样本 $z\in R^d$ 转化成生成样本 $G\left(z\right)$ 。判别器 $D$ 视图将它们与来自分布 $\mu$ 的真实训练样本区分开来，而 $G$ 试图使生成样本在分布上与训练样本相似。对抗的目标损失函数如式2-1所示为:

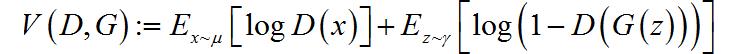
  在式2-1中，E表示关于下表中指定分布的期望值。GAN可以通过一个极大极小值问题的形式解决，如式2-2所示:

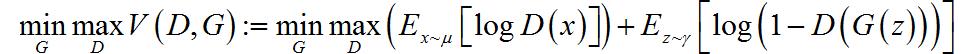
  直观理解式 2-2,对于给定的生成器 $G,{\max }_{D}V\left(D,G\right)$ 优化判别器 $D$ 以区分生成样 $G\left(z\right)$ ，即分布 $\mu$ 的真实样本权重更大，而生成样本 $G\left(z\right)$ 的权重更小。相反，对于给定的鉴别器 $D,{\min }_{G}V\left(D,G\right)$ ，优化 $G$ ，使得生成样本 $G\left(z\right)$ 可以互动判别器 $D$ 以分配更大权重。设 $y=G\left(z\right)\in R^n$ ，其分布为 $\upsilon :=\gamma \cdot G^{-1}$ ，可以使的 $D$ 和 $\upsilon$ 重写 $V\left(D,G\right)$ 为2-3式

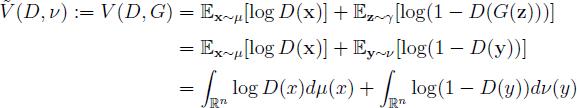
  将式2-2中的极大极小值公式变为式2-4:

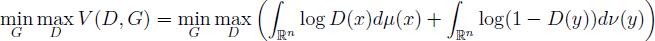
  如果在每个训练周期中，允许判别器 D达到其给定最佳 q(x)，然后更新 q(x)，根据最小化准则有式2-5:

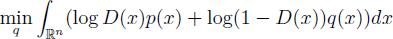
  综上可以总结得出 GAN的算法求解如下:

• Input:随机噪声 z1,…, zmin Rd;真实样本 x1,…, xm⊂X.
• Output:生成样本Xfake.

  1. for t =0 to T −1 do
  2. 从高斯噪声分布γ中随机