Java版高级数据结构赫夫曼树(哈夫曼树)

Posted 2022-02-06 chenry777

本文代码地址： https://github.com/chenruoyu0319/data-structure-for-java/tree/main/%E8%B5%AB%E5%A4%AB%E6%9B%BC%E6%A0%91(%E5%93%88%E5%A4%AB%E6%9B%BC%E6%A0%91)

一、赫夫曼树（哈夫曼树）

首先让我们来思考2个问题：

1.电报发送：二战的时候大家都知道那时候普遍会应用电报，如果让你来设计一个电报的发送编码你该如何设计呢？

一种思路就是做一个映射，比如a b c d ，a映射到22525， b映射到3333，c映射到56，d映射到78，

那么abcd => 2252533335678

这样就能实现我们的需求，也就是一个可逆的加密

2.压缩(通信)算法：给你10000个字符（每个字符1byte，也就是8bit）的文件，你怎么存储(通信)可以尽可能的节省空间呢？

我相信大家肯定能想到的一个思路就是用某个字符来代替（映射）。比如在压缩算法里面我们可以用二进制来代替具体的字符。

假设字符是 a b c d 4种

那我们假定 a=000 b=001 c=010 d=100,这样我们每个字符就变成了3bit的二进制，那么10000个字符就是30000bit，比起原来的80000bit是不是缩小了很多的存储空间？缩小了将近3倍。

但是这样等位数的设置映射关系，会导致字符数多的情况下，每个字符所对应的二进制长度过长，那么有没有什么优化的思路呢？是有的。

比如我们可以以如下的方式设置编码映射：

a: 0

b: 101

c: 110

d: 100

adbcaaaaaaaaa：010111010000000000

这种编码方式被称为：前缀编码，也叫做赫夫曼编码。他的特性是：某字符出现的越多，编码越短，短编码避开长编码的前缀，即任何编码值不能是其他值的前缀。

二、最优二叉树（赫夫曼树）

最优二叉树又被称为赫夫曼树。

下面让我们来试着计算下面三颗二叉树的带权路径长度总和：

其中每个点的权重为：

a:7 b:5 c:2 d:4

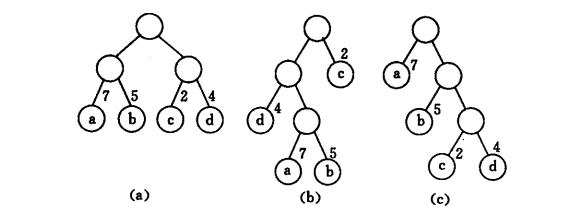
WPL(a): 7*2+5*2+2*2+4*2=36

WPL(b): 7*3+5*3+2*1+4*\\2=46

WPL©: 7*1+5*\\2+2*3+4*\\3=35

其中c树的带权路径总和最小，这样的树就是最优二叉树。

构建一棵最优二叉树的核心思想就是用的贪心算法：利用局部最优推出全局最优，把频率出现多的用短码表示，频率出现小的就用长一点表示。而且，任何一个字符的编码都不是另一个的前缀，在解压缩的时候，我们每次会读取尽可能长的可解压的二进制串，所以在解压缩的时候也不会产生歧义。

具体实现思路：

1.每次取数值最小的两个节点，将之组成为一颗子树。

2.移除原来的两个点

3.然后将组成的子树放入原来的序列中

4.重复执行1 2 3 直到只剩最后一个点

我们来计算一个例子： a:3 b:24 c:6 d:20 e:34 f:4 g:12

根据以上权重来实现赫夫曼树，代码见github

三、小结

学完赫夫曼树，现在可以回到我们的思考题，这两个问题就迎刃而解了。

一、电报的设计：使用赫夫曼树

1.电报加密后越短越好，发送快。

2.破解难

3.解码容易

4.换加密树也要快

5.可逆的。

二、数字通信和压缩：也可以使用赫夫曼树，不过要注意有一些稀疏的文件没办法压缩太多

，发送快。

2.破解难

3.解码容易

4.换加密树也要快

5.可逆的。

二、数字通信和压缩：也可以使用赫夫曼树，不过要注意有一些稀疏的文件没办法压缩太多