牛客-[NOIP2018]货币系统——完全背包问题的贪心优化

Posted 2022-02-06 C+++++++++++++++++++

文章目录

• • 题目
  • 题目解析
  • 解题代码

题目

题目链接

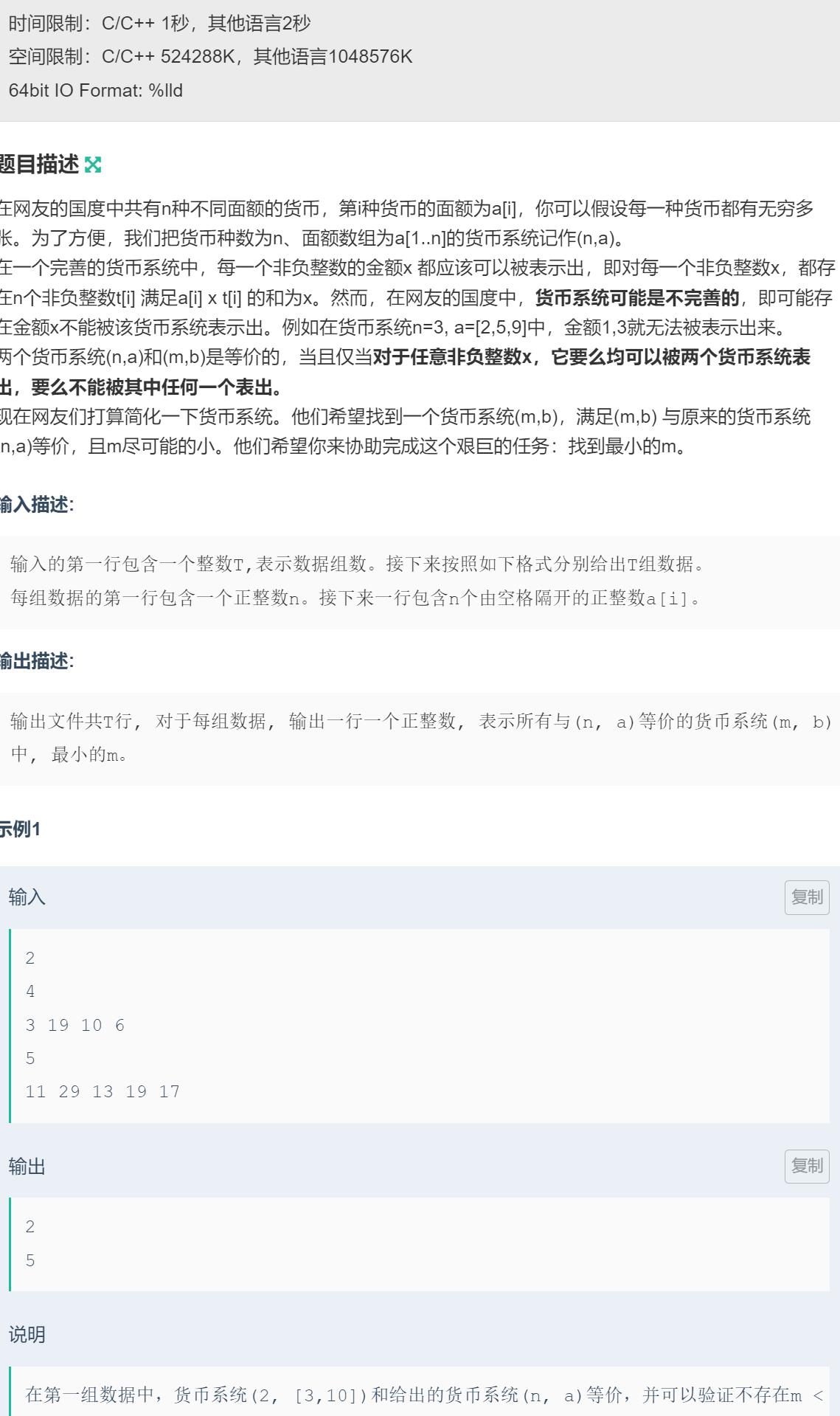
题目解析

首先你要清楚这个等价货币系统是这么看的。

等价货币系统，实际上就是把里面多余的面值给去掉。那么什么时候面值会多余呢？当然是内部面值能够被当前面值拼出来啊。

所以我们可以采取背包策略判断一个面值系统的每一个数是否能被拼出，如果能则该面值可以舍去。

但回头一想，这样完全暴力的处理方法，你会发现你每次都要重新去计算这个背包的 O(n*m) 的复杂度，而明明是同一个面值系统。这就导致计算一个面值系统的都得花 O(n*n*m) 的复杂度，所以完全可以通过贪心思想将其优化为原本的 O(n*m) 复杂度，也就是只计算一次背包即可！由于内部的面值想要被拼出，那么只能被比它小的面值拼出，所以我们先进行一次排序，然后再进行完全背包即可，这样处理后，每次轮到某个面值进行背包，那么它的能否被拼出的结果肯定就已经被计算好了，所以直接可以得出是否需要舍去！

但实际上完全暴力的背包方式也能过，我只是提供一个更舒服的优化方式，这样再加测试用例，也能快速通过了！

比如下面这样的暴力记忆化它也是能过的：

#include <bits/stdc++.h>
using namespace std;
int memo[25005];
int nums[105];
int t,n;
int skip;//TODO 标记需要跳过的数
bool dp(int val)
    if(val==0)
        return true;
    if(val<0)return false;
    if(memo[val]!=-1)return memo[val];
    for(int i=0;i<n;i++)
    
        if(nums[i] == skip)
            continue;
        if(dp(val-nums[i]))
            return true;
    
    return memo[val] = false;

int main () 
    ios::sync_with_stdio(false);
    cin>>t;
    while (t--)
        cin>>n;
        for(int i=0;i<n;i++)
            cin>>nums[i];
        
        int cnt = 0;
        for (int j = 0; j < n; ++j) 
            memset(memo,0xff,sizeof(memo));
            skip = nums[j];
            if(!dp(nums[j]))
                cnt++;
        
        cout<<cnt<<'\\n';
    
    return 0;

解题代码

#include<bits/stdc++.h>
using namespace std;
const int M=25100;

int a[110];
bool dp[M];

int main() 
    ios::sync_with_stdio(false);
    int _;
    for(cin>>_;_;_--) 
        int n;cin>>n;
        for(int i=1;i<=n;i++) cin>>a[i];
        memset(dp,false,sizeof(dp));
        dp[0]=true;//初始条件
        //TODO 排序的意义：
        // 让完全背包从最小的开始更新，而大的肯定只能被小的拼出来，
        // 所以到了某个货币时，实际上已经把内部货币能否构成它的所有情况计算完了。
        // 故一旦能够被内部拼出来，那么直接跳过计数
        sort(a+1,a+n+1);
        int ans=0;
        for(int i=1;i<=n;i++) 
            if(dp[a[i]]) continue;
            ans++;
            for(int j=a[i];j<M;j++) 
                dp[j]|=dp[j-a[i]];//当前是3 ，0是否出现 若
                                 //若出现标记3
        
        cout<<ans<<'\\n';