[FJWC2018]欧拉函数

Posted 2022-02-06 StaroForgin

欧拉函数

题目描述

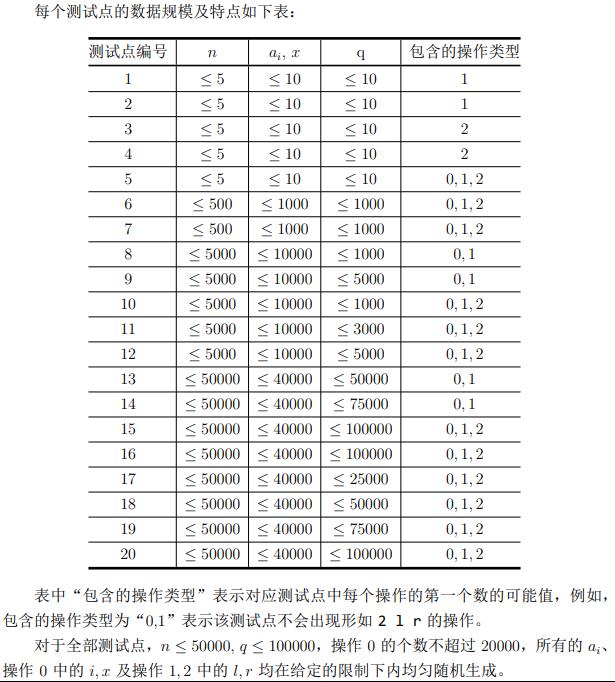
题解

首先，我们关注到这一题最重要的一点是保证所有的$a,i,x,l,r$均随机生成。
对于操作$1$，每次询问的区间和大小期望大概是$\frac{na}{4}\approx 5\times 10^8$，区间的和。
如果我们暴力算欧拉函数大概是$O(\sqrt{\frac{5\times 10^8}{\log 5\times 10^8}}\approx 4152.3)$的，对于$q=10^5$，应该也勉强能过。
由于总和是随机的，所以应该也不需要所有质数都跑完，会更快一点。
关键是操作$2$，对于乘法我们又该怎样统计。
由于随机生成，所以我们可以猜测每个数所拥有的大于$30$的质因子个数应该比较少，每个数大概期望有$1.05$个。
故我们很快可以想到将小于$30$的质数贡献与大于$30$的质数贡献分别进行处理。

对于小于$30$的质数，由于个数比较小，我们可以考虑用线段树单独维护每个质因子的出现次数。
由于欧拉函数是积性函数，所以我们显然可以对于单个质因子分别统计欧拉函数值，最后乘起来。
询问$2$查询时就直接查询区间内这部分质数出现了多少个，计算该质数贡献的欧拉函数就行了，大概是$O\left(10\log n\right)$的。

对于大于$30$的质数，由于本身就比较多，相同质因子的应该也比较分散。
对于一个数的质因子$p$，如果它前面有数也存在$p$的质因子，那么它的贡献时$p$，否则是$p-1$。
对于前面是否存在数有质因子$p$，显然我们只需要看离它最近的一个$p$是不是在我们查询的区间范围内。
我们在查询到它的时候可以在前面的$p$的位置放上一个$\frac{p}{p-1}$，在它原来的位置就放$p-1$，查询左边界的后缀积，显然只会在包含前面的哪个位置时它的贡献才会是$p$，否则其贡献为$p-1$。
这种技巧我们应该是在前面的题中见到过得，但我懒得找了。
但如果我们真的一个一个去查询的话显然太慢了，每一个都得拿一个数据结构维护，我们不妨考虑分块。
对于块内的点，如果它们不存在大于$30$的公共质因子，显然它们之间是独立的，我们完全可以将它们维护的这个贡献给放在一起。
如果同一个块内两个数有着相同的质因子$p-1$，显然后面那一个是不可能产生$p-1$的贡献的，我们就将这个整块的贡献乘上$p(p-1)$，再在前一个数的前一个相同质因子位置上放上$\frac{p}{p-1}$就行了。
这样的话，我们对于一个整块就只需要维护一个数据结构了，这个数据结构采用树状数组就行了。
对于散块的点，我们需要知道的是它们前面是否有与它相同的质因子的数，这个数既可能来自整块的数，也有了能来自散块的数。
散块的数就直接将它们大于$30$的质因子记录下来就行了，对于整块，我们可以去记录一下整块的数关于大于$30$的每个质数的前缀和，通过差分找到我们现在的这个质数是否出现。
由于我们的修改次数是比较少的，我们可以在每次修改后暴力修正修改的这个质数的前缀和。
同时修改时对于整块我们可能会影响它自身与它相同质因子的后面最近的点关于整块数据结构内的贡献。
可以用$set$维护它后面的点是哪一个，然后暴力在数据结构上更改。
这样就很容易计算出整块与散块的贡献了，与小于$30$质数的贡献乘在一起就行了。

记我们进行了$m$次$0$类操作，有$P$个质数，$S$为块长，时间复杂度$O\left(\frac{n}{S}P+m(\frac{n}{S}+10\log n)+q(10\log n+S+\frac{n}{S}\log n)⩾O\left(10(m+q)\log n+q\sqrt{n\log n}\right)\right)$，显然可以过。

源码

有点卡常。

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
using namespace std;
#define MAXN 50005
#define MAXM 500005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long LL;
typedef unsigned long long uLL; 
typedef long double ld;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int mo=1e9+7;
const int mod=1e5+3;
const int inv2=5e8+4;
const int jzm=2333;
const int zero=20000;
const int n1=400;
const int orG=3,ivG=332748118;
const long double Pi=acos(-1.0);
const double eps=1e-12;
template<typename _T>
_T Fabs(_T x)return x<0?-x:x;
char gc()static char buf[1000000],*p1=buf,*p2=buf;return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
#define getchar gc
char obuf[1<<22],*opt=obuf+(1<<22);
void pc(const int&ch)*--opt=ch;
#define putchar pc
template<typename _T>
void read(_T &x)
	_T f=1;x=0;char s=getchar();
	while(s>'9'||s<'0')if(s=='-')f=-1;s=getchar();
	while('0'<=s&&s<='9')x=(x<<3)+(x<<1)+(s^48);s=getchar();
	x*=f;

template<typename _T>
void print(_T x)putchar('\\n');while(x>9)putchar((x%10)|'0');x/=10;putchar(x|'0');
int gcd(int a,int b)return !b?a:gcd(b,a%b);
int add(int x,int y,int p)return x+y<p?x+y:x+y-p;
void Add(int &x,int y,int p)x=add(x,y,p);
int qkpow(int a,int s,int p)int t=1;while(s)if(s&1)t=1ll*t*a%p;a=1ll*a*a%p;s>>=1;return t;
const int M=255;
int n,q,a[MAXN],prime[MAXN],cntp,ff[MAXN],sta[MAXN],stak,tur[MAXN];
int block[MAXN],L[MAXN],R[MAXN]
以上是关于[FJWC2018]欧拉函数的主要内容，如果未能解决你的问题，请参考以下文章
 
 51nod1239 欧拉函数之和
 FJWC2020 题解合(gu)集(gu)
 fjwc2019 D2T2 定价 （栈+set+贪心）
 fjwc2019 D1T1 （dp+树状数组）
 fjwc2019 D3T1 签到题 （贪心）
 fjwc2019 D6T1 堆（组合数+打表）