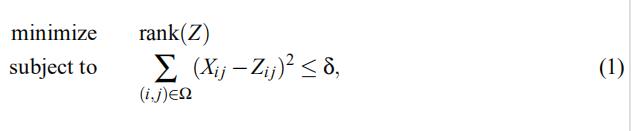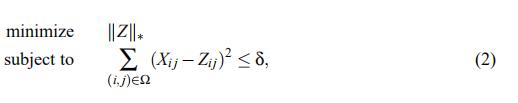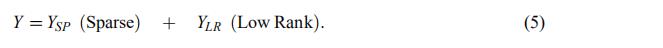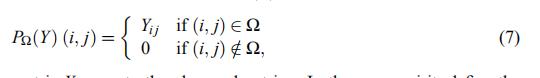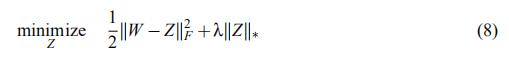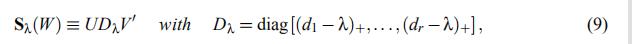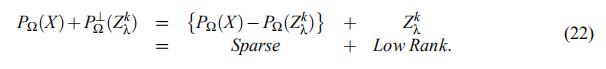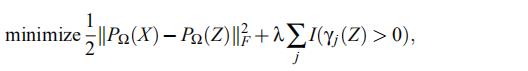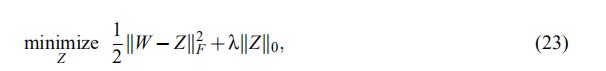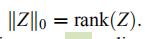论文笔记 Spectral Regularization Algorithms for Learning Large IncompleteMatrices （soft-impute）

Posted 2022-02-05 UQI-LIUWJ

2010 JMLR

0 摘要

        使用凸松弛技术为大规模矩阵完成问题提供一系列正则化低秩解决方案。

论文算法 SOFT-IMPUTE 迭代地用从软阈值 SVD 获得的元素替换缺失的元素。通过热启动，这使算法能够有效地计算正则化参数值网格上解决方案的整个正则化路径。

1 introduction

表示观测矩阵，最早的矩阵补全问题的优化目标函数为：

δ表示训练误差的容忍程度（一个正则项参数）

 由于rank(Z)非凸，所以后续文献对(1)进行了一定的修改

 这里||Z||*表示核范数（是Z的奇异值的和）

用拉格朗日算子表达（3），有：

 

         在本文中，我们为核范数正则化最小二乘问题 (3) 提出了一种SOFT-IMPUTE算法 ，该算法可扩展到 m,n ≈的大型问题，其中观察到的条目约为 或更多。 在每次迭代中，SOFT-IMPUTE 将目标函数的值降低.

2 相关工作

        最早期矩阵补全问题的目标函数为

         也即相当于（1）中δ=0。但是这种评判标准太过于严苛，同时会导致一定的过拟合，于是便有了（1）中的目标函数

         在本文中，我们提供了一种 SOFT-IMPUTE算法，用于基于热重启的方式计算 (3) 的优化目标函数。

        该算法的灵感来自 SVD-IMPUTE迭代算法，它使用“ 完整的”数据矩阵，在当前 SVD中 补全缺失值。

        这种迭代算法要求在每次迭代时计算密集矩阵（维度等于矩阵 X 的大小）的 SVD。这是这种迭代算法的瓶颈所在：无法进行大规模计算。

        本篇论文的算法 SOFT-IMPUTE 也需要在每次迭代时进行 SVD 计算，但SOFT-IMPUTE 通过利用问题结构，可以轻松处理非常大维度的矩阵。

        在每次迭代中，非稀疏矩阵具有以下结构：        

         其中Ysp具有和观测矩阵X一样的稀疏结构，有一个远小于观测矩阵X 维度m和n的秩r' （算法收敛时，r'很接近于预测矩阵Z的秩）

 另一种使用协同过滤的方法使用矩阵分解，他被称为MMMF（maximum margin matrix factorization methods）

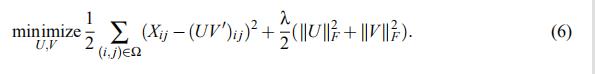
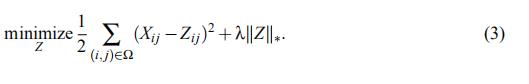
        事实证明，（6）与（3）密切相关。如果Z的秩 r′ = min(m,n)，则 (6) 的解与 (3) 的解一致。2 然而，(6) 在其自变量中不是凸的，而 (3) 是

3 SOFT-IMPUTE

3.1 符号说明

投影函数	如果有观测值的地方就是Yij，没有观测值的地方就是0    ——>可以写成
互补投影	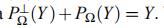（Y有观测值的部分，Y没有观测值的部分）

 3.2 核范数正则化

我们提出了以下引理，它构成了我们算法的基本要素。

假设矩阵的秩是r，

那么

结果可以由 得到

 

 

UDV'是W的SVD分解 

d1,....,dr是D的对角元素

t+=max(t,0)

Sλ表示 soft-thresholding

使用3.1的表示，我们可以改写（8）为

 

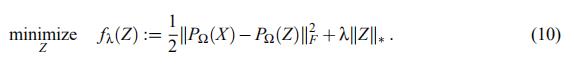
 3.3 算法

        我们现在提出 SOFT-IMPUTE算法 —— 用于计算 (10) 的一系列解决方案，用于使用暖启动的不同 λ 值。

每过一段时间，λ缩小一点，这样也能越来越精细

如何理解前面的(5)呢

3.4 和MMMF的关联

论文的附录部分证明了一个引理

 

 所以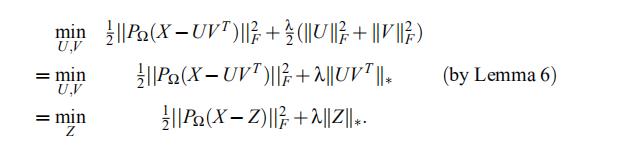

 

4 收敛性分析

暂略 

5 计算复杂度

暂略

6 从软阈值到硬阈值

        我们认为，在许多问题中，ℓ1 正则化也可以提供更好的预测精度。（软阈值）

         但是，如果观测模型非常稀疏，则具有均匀收缩的 LASSO范数（L1正则化） 既会高估模型中非零系数的数量，也会过度收缩（偏向）包括向零的系数

        所以论文又提出了硬阈值的方法

        这里表示Z的第j个奇异值

        我们用矩阵的形式表示，可以写成

 

        这里

 和软阈值时候类似，也可以用一个SVD 来解决上述优化问题

对于每个特定的λ，有相应的q=q(λ)个奇异值被保留

 

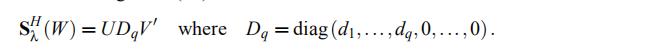
 6.1 硬阈值算法

和软阈值类似，也是一个迭代算法

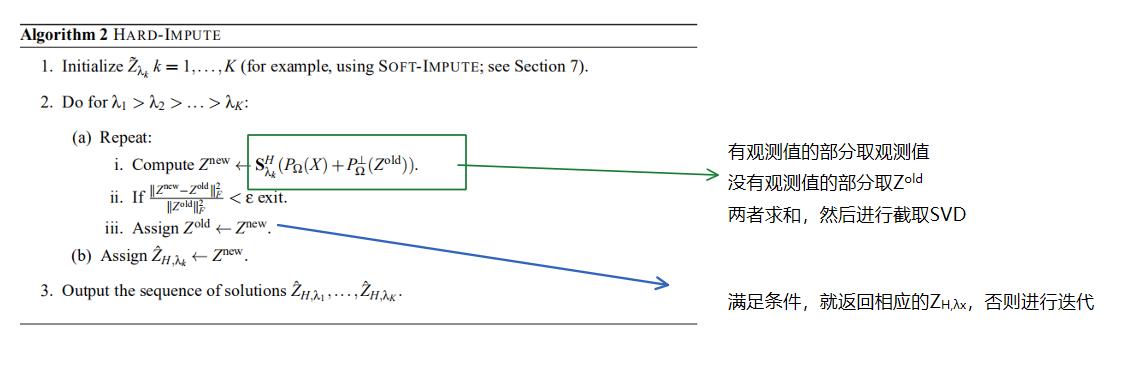
 这也就是这里提到的迭代算法

推荐系统笔记：基于SVD的协同过滤_UQI-LIUWJ的博客-CSDN博客_基于svd的协同过滤