自动驾驶 11-3: 根据 LIDAR 数据进行位姿估计 Pose Estimation from LIDAR Data

Posted 2022-02-04 AI架构师易筋

既然你已经学会了如何翻译， 旋转和缩放点云， 是时候谈谈我们该如何做 实际使用这些操作 用真实的点云 估计自动驾驶汽车的运动。

我们这样做的方式 一般是通过解决某事 称为点集配准问题， 这是最重要的问题之一 在计算机视觉和模式识别方面。

在这个视频结束时， 你将能够描述点集 注册问题以及如何 它可以用于状态估计， 描述和实现迭代最近点 或用于点集配准的 ICP 算法， 并了解一些常见的使用陷阱 用于自动驾驶汽车状态估计的 ICP。

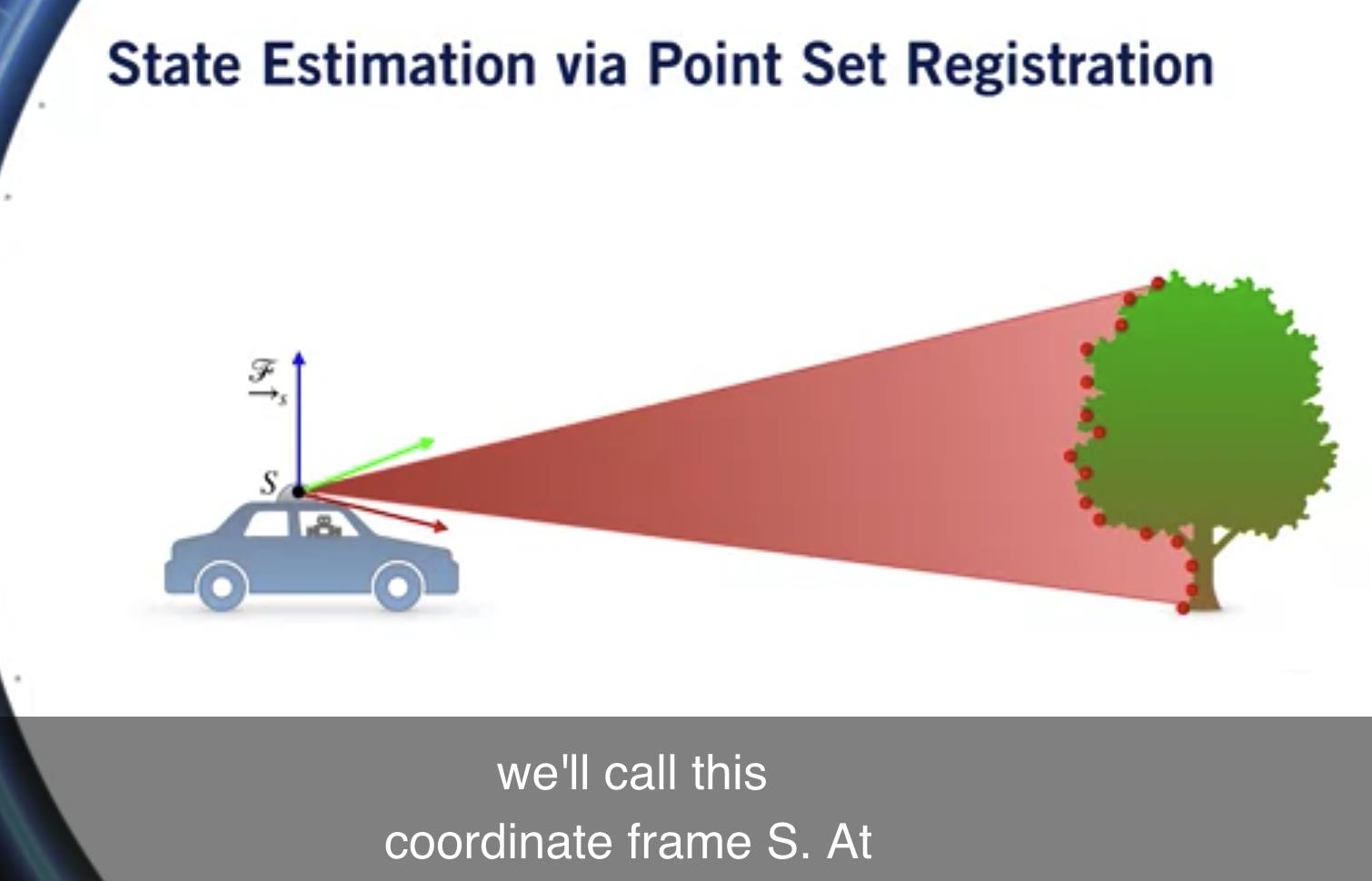
让我们回到我们的例子来探讨这个问题 一辆自动驾驶汽车观察 来自安装在车顶上的激光雷达的一棵树。

在时间 t 等于一个说， 激光雷达返回一个点云 像以前一样遵循树的轮廓。

每个点的坐标 在点云中给出 相对于姿势 扫描时的激光雷达， 我们称这个坐标系为 S。

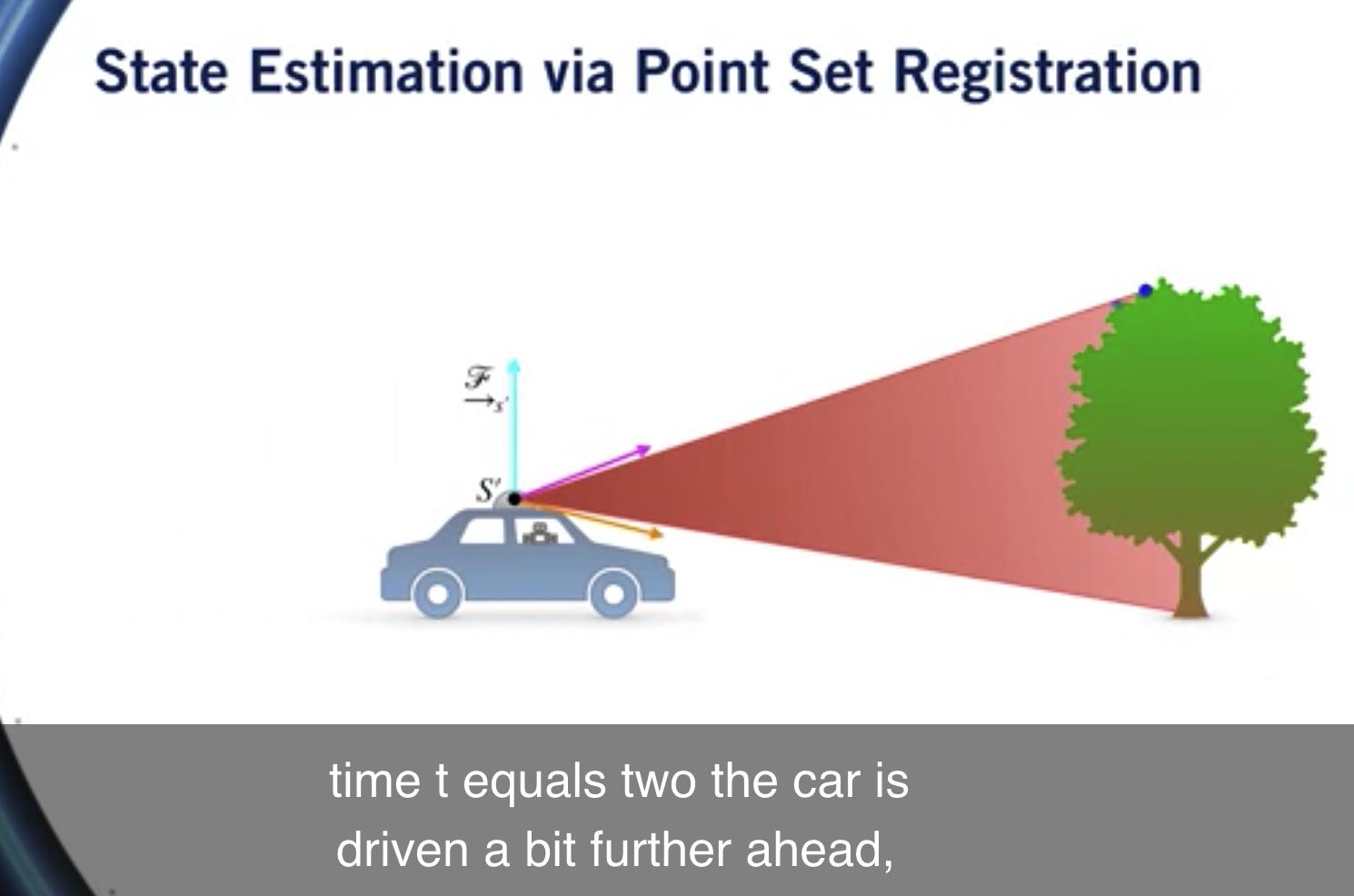
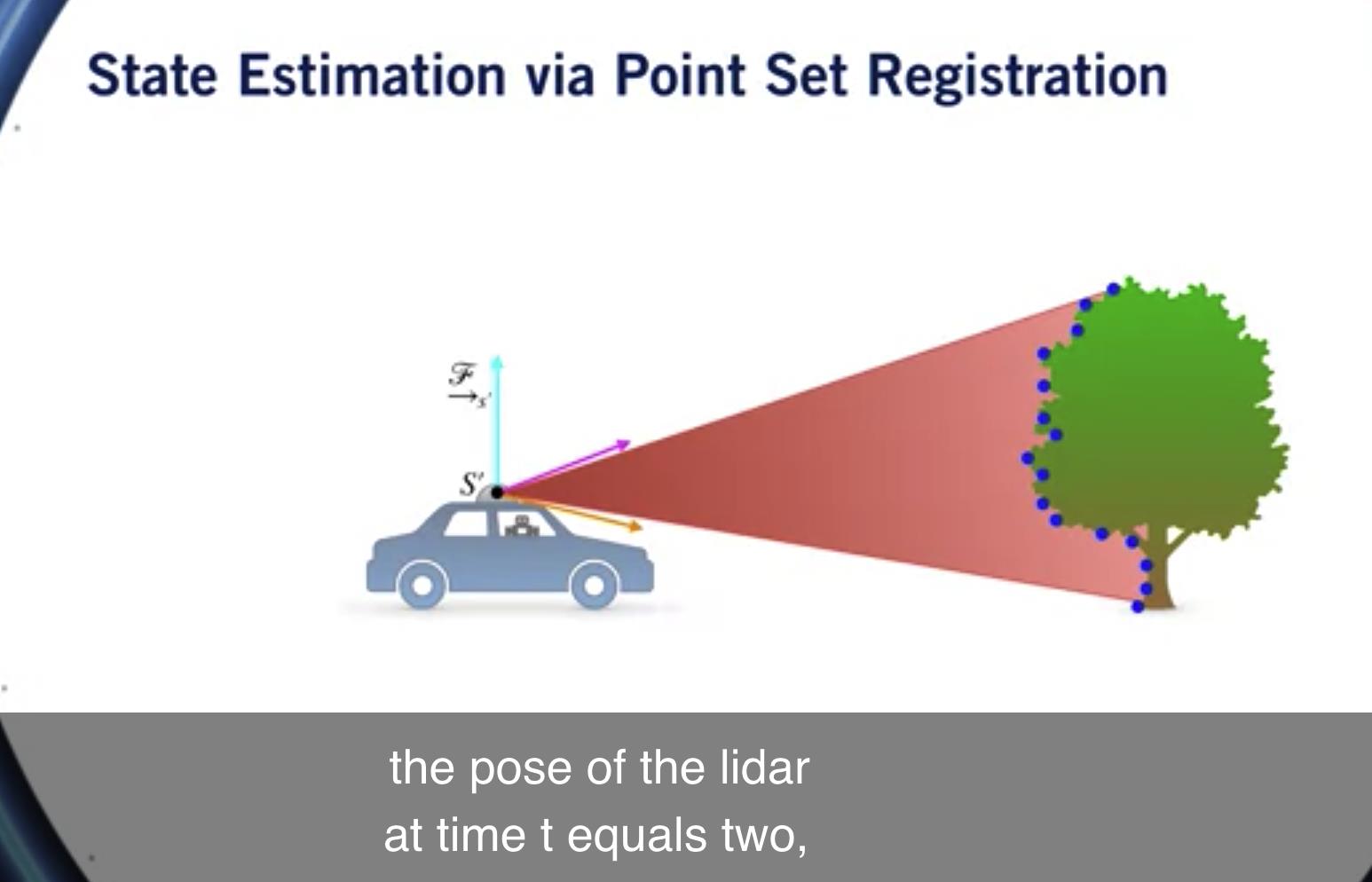
在 时间 t 等于 2 汽车向前行驶了一点， 但激光雷达仍然可以看到树 并返回第二个点云 其坐标再次相对于 激光雷达在时间 t 的位姿等于 2， 我们称这个坐标系为 S 素数。

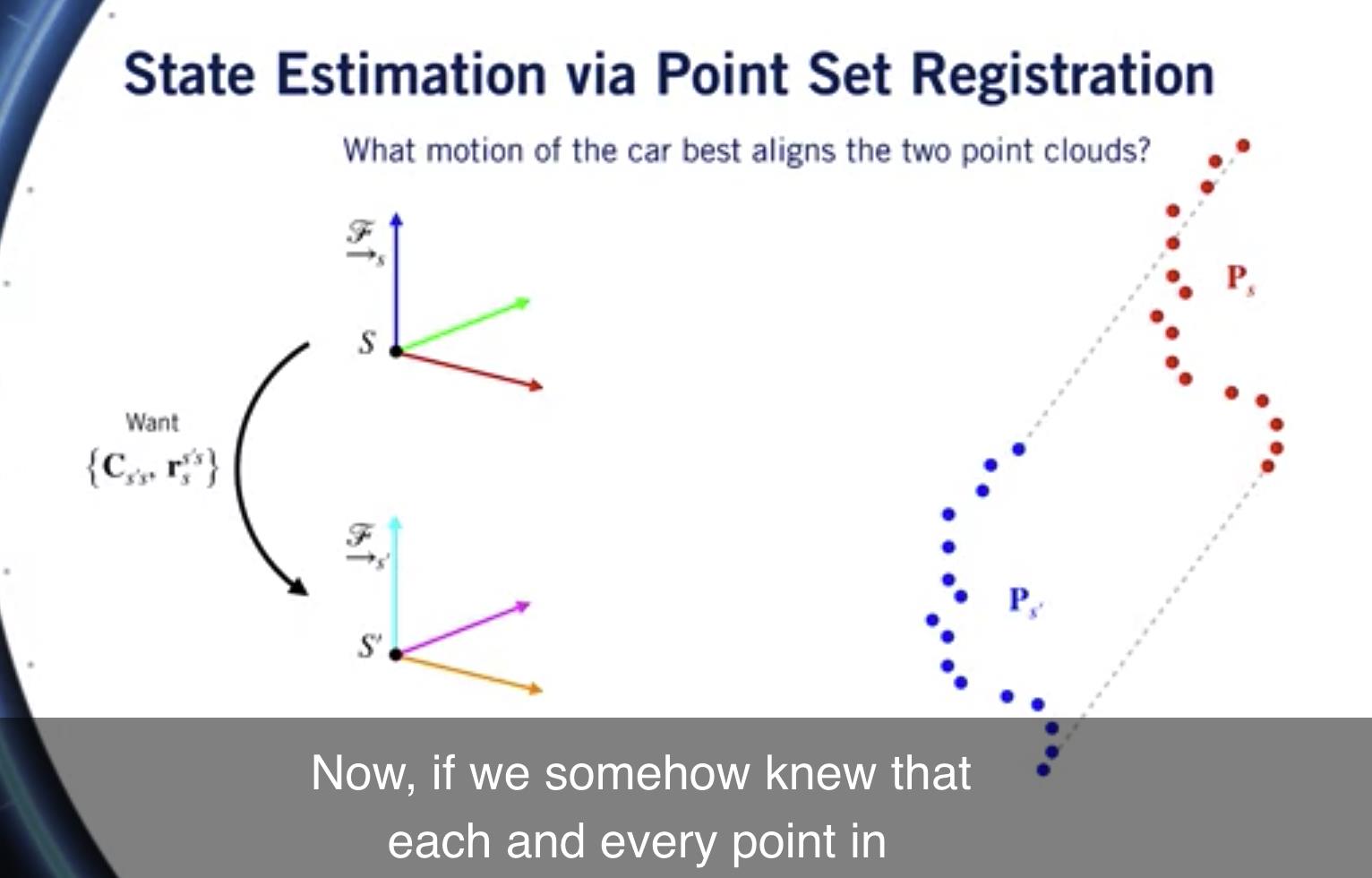
现在，点集注册问题说， 给定两个不同坐标系中的 2 个点云， 并且知道它们对应于 或包含世界上相同的对象， 我们将如何对齐它们以确定传感器如何 必须在两次扫描之间移动？

更具体地说，我们想弄清楚 出最优翻译和 之间的最佳旋转 两个传感器参考框架 最小化两个点云之间的距离。

我们将很快描述距离的含义。

为了简单起见， 我们将假装我们有一个理想的激光雷达传感器 一次测量整个点云， 这样我们就可以忽略运动失真的影响。

现在，如果我们以某种方式知道 第二个点云对应于 第一个点云中的特定点， 我们提前知道 哪个点对应哪个， 我们可以轻松解决这个问题。

我们所要做的就是找到翻译和 将每个点与其双胞胎对齐的旋转。

在这个例子中，我们理想的旋转矩阵 将是单位矩阵， 那根本不是旋转， 理想的翻译是 沿着汽车前进的方向。

问题是，一般来说，我们 不知道哪些点相互对应。

在计算机视觉课程中， 您将了解特征匹配 这是确定的一种方法 使用cameraData的点之间的对应关系。

但现在让我们考虑一下如何解决 这个问题不知 任何通信提前。

最流行的算法 解决这类问题称为 迭代最近点算法或简称ICP。

ICP背后的基本直觉是这样的， 当我们找到最佳平移和旋转时， 或者如果我们事先知道一些关于他们的事情， 我们用它们来改造 一个点云进入另一个点云的坐标系， 真正的点对 相互对应将是 最接近每个的 欧几里得意义上的其他。

这是有道理的，如果你考虑 我们的激光雷达传感器的简化案例 扫描完全相同的点 只是从两个不同的角度。

在这种情况下，有一个一对一 两次扫描中的点之间的映射， 而且这个映射完全 由传感器的运动决定。

所以，这是我们发现的理想情况 最好的平移和旋转， 但是如果我们没有怎么办 最佳平移和旋转， 我们如何决定哪些点实际上是在一起的？

好吧，对于 ICP，我们使用一个简单的启发式算法， 并说对于一朵云中的每个点， 对应点的最佳候选者 另一个云是重点 现在最接近它。

这里的想法是，这种启发式 应该给我们的通信 让我们做下一个猜测 对于平移和旋转， 这比我们目前的猜测要好一点。

随着我们的猜测越来越好， 我们的通信也应该 越来越好，直到我们 最终收敛到最优运动 和最佳对应关系。

这种迭代优化方案使用 最接近点启发式是 ICP 得名的地方。

重要的是要注意这个词 最接近意味着我们将找到点 之后靠得很近 仅应用帧到帧转换。

也就是说，因为车辆是 搬家几乎从来不是这样 激光束会击中 完全相同的表面点两次。

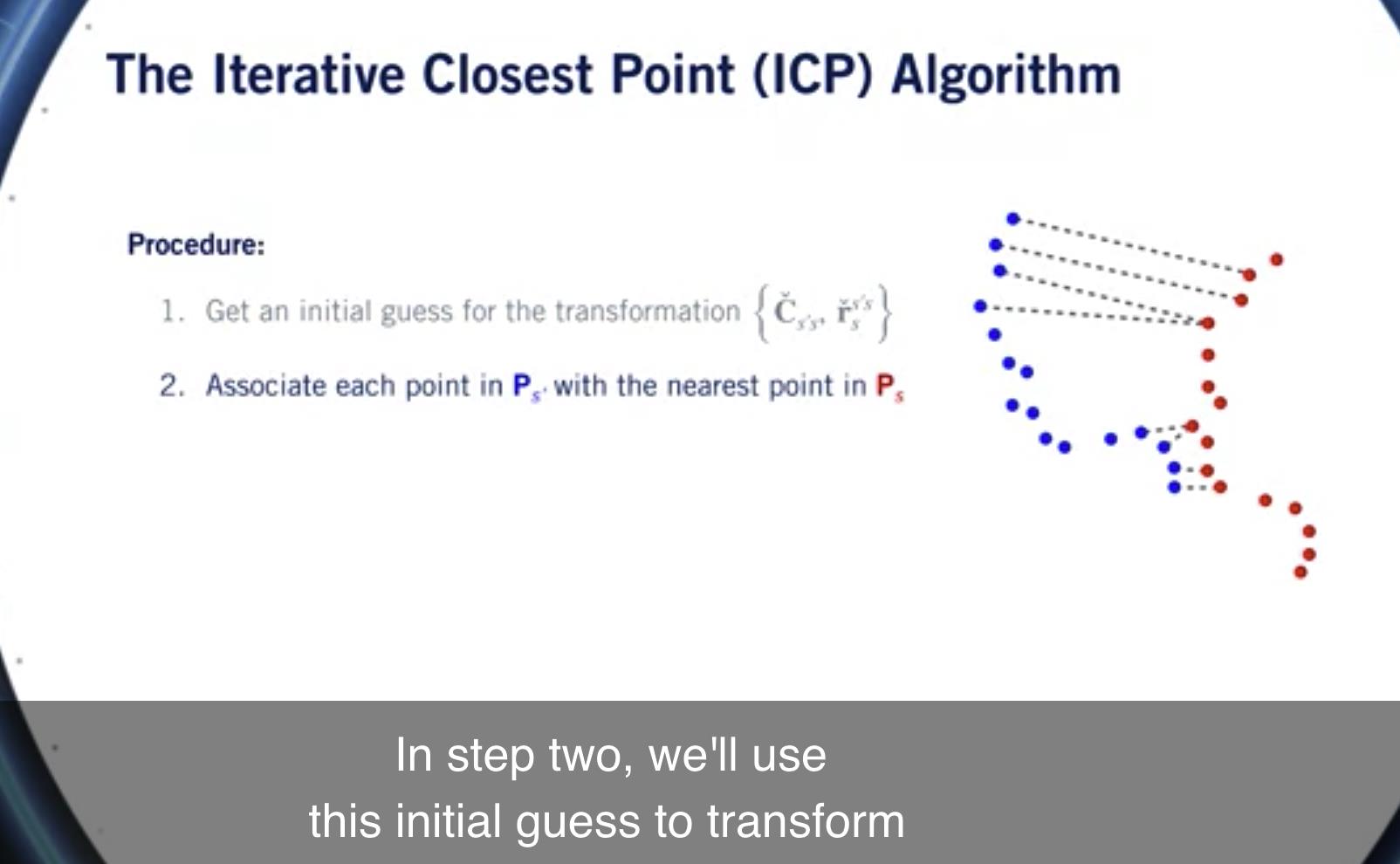
那么，让我们谈谈ICP算法中的步骤。

首先也是最重要的是我们 需要对转换进行初步猜测。

我们需要这个，因为无法保证 最近点启发式将 实际上收敛到最佳解决方案。

很容易陷入局部最小值 在这些迭代优化方案中。

所以，我们需要一个好的开始猜测。

现在，最初的猜测可能来自多个来源。

最常见的来源之一 自动驾驶等机器人应用 是一个运动模型， 可以由 IMU 提供 我们在上一个模块中看到或通过 车轮里程计或非常简单的东西 比如恒速甚至零速模型。

运动模型需要多复杂才能给我们 一个很好的初步猜测 取决于汽车行驶的顺畅程度。

如果汽车相对缓慢地移动 激光雷达传感器的扫描速率， 甚至可以使用 最后一个已知的姿势作为初始猜测。

对于我们的示例，假设我们使用 一个非常嘈杂的 IMU 和 情感模型提供初始猜测。

模型告诉我们传感器翻译了 向前一点，也向上倾斜。

在第二步中，我们将使用这个初始猜测来转换 中点的坐标 一朵云进入另一朵云的参考系， 然后匹配每个点 第二朵云到第一朵云中最近的点。

在这里，我们展示了 前四分和后四分。

请注意，没有什么能阻止两个点 与一朵云相关联 另一朵云中的同一点。

第三步是把所有的 那些匹配点并找到转换 最小化总和 对应点之间的平方距离。

我们稍后会讨论这一步背后的数学原理， 但你可以把它想象成包装 每对匹配点周围都有一条松紧带， 然后放手等待系统 找到它的最低能量配置。

与相关的平移和旋转 这种最小能量配置 是最优解。

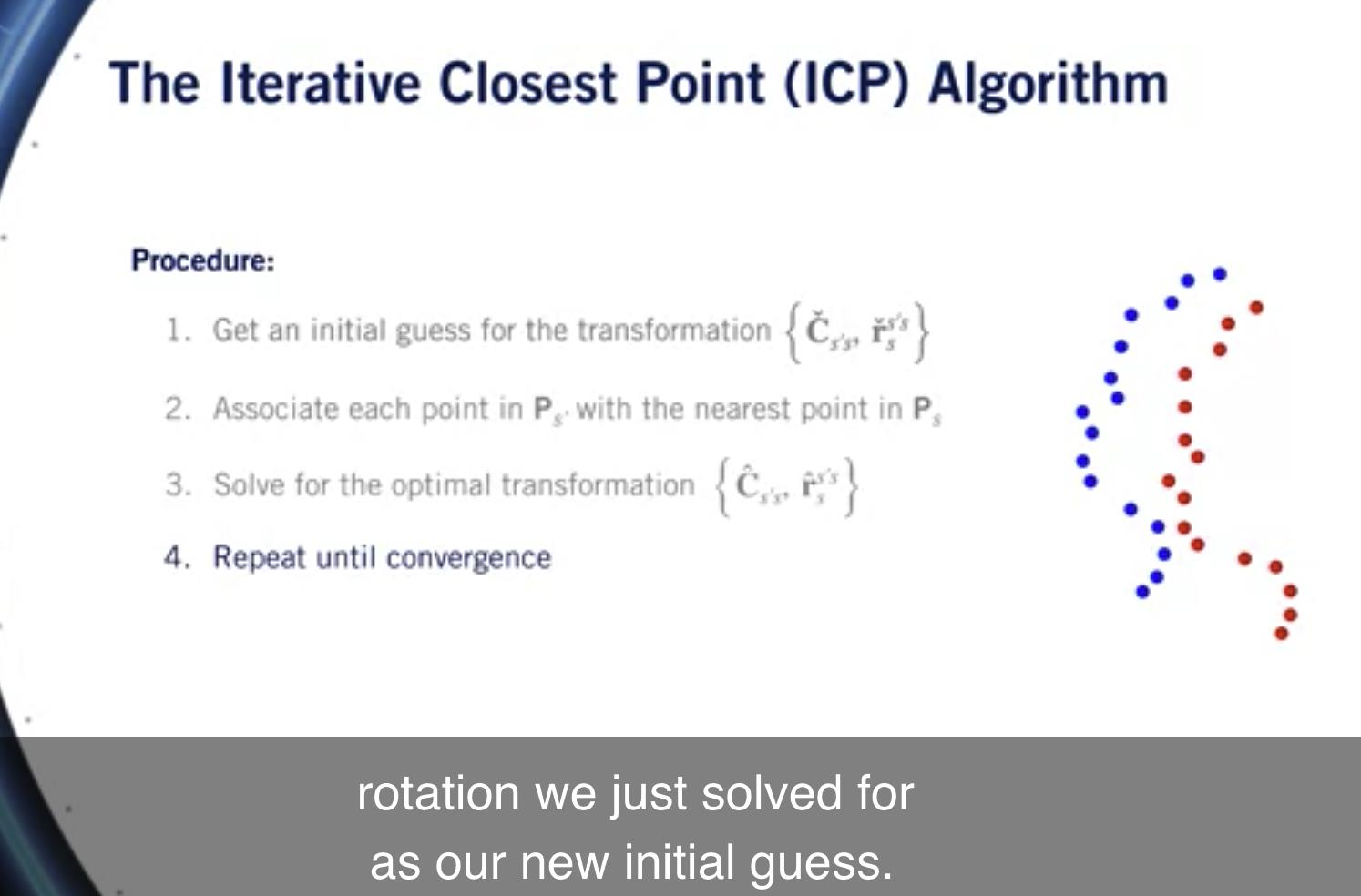
然后，我们使用翻译和重复该过程 我们刚刚解决的旋转作为我们新的初始猜测。

我们继续前进，直到优化收敛。

所以在下一次迭代中， 我们使用新的平移和旋转来变换 点云，然后找到最接近的匹配， 求解最优变换， 并继续前进，直到我们到达 多次迭代后最优。

我们如何实际解决 第三步的最优转换？

也许你已经猜到我们将使用 我们最喜欢的工具，最小二乘法。

我们的目标是找到旋转和 最能对齐两个点云的平移。

具体来说，您希望最小化 之间的平方欧几里得距离 每对匹配点， 这是损失函数之一 我们在这里定义的。

这个最小二乘问题有点多 比我们迄今为止遇到的复杂。

那是因为旋转矩阵 在损失函数内部。

原来是旋转矩阵 不要表现得像向量。

如果将两个向量相加， 你得到另一个向量。

但是如果你把两个旋转矩阵加在一起， 结果不一定是有效的旋转矩阵。

实际上，3D 旋转属于一种叫做 特殊正交群或 SO3。

在本课程中，我们不会深入研究这意味着什么， 但重要的是要记住 旋转需要特殊处理。

事实证明，有一个很好的封闭形式解决方案 这个最小二乘问题是 发现于 1960 年代。

我们不会在这里进行推导， 但好消息是 一个简单的四步算法 你可以按照来解决这个问题。

前两个步骤很简单。

首先，我们计算质心 每个点云通过采取 每个点坐标的平均值。

这就像计算 物理学中的质心。

其次，我们在一个三乘三矩阵上工作 捕捉两个点云的传播。

你可以把这个 W 矩阵想象成 您可能会在力学中遇到的惯性矩阵。

W矩阵是我们要使用的数量 估计最优旋转矩阵。

第三步实际上是寻找 最优旋转矩阵。

这一步是最复杂的， 它涉及采取一种叫做 W 矩阵的奇异值分解或 SVD。

如果您以前从未见过 SVD， 这一步可能看起来有点神奇。

让我们花点时间谈谈什么 奇异值分解确实如此。

SVD是一种分解方式 一个矩阵到两个酉矩阵的乘积， U 和 V，以及对角矩阵 S， 其非零条目称为 原始矩阵的奇异值。

有几种方法可以解释 SVD。

但对我们来说，最容易将 U 和 V 视为 旋转和 S 矩阵作为缩放矩阵。

因为我们正在处理刚性 在这个问题中的身体运动， 我们不希望在旋转估计中进行任何缩放， 所以我们将用一些东西替换 S 矩阵 像单位矩阵一样消除缩放。

我们选择的方式有一个技巧 新缩放矩阵的右下角条目。

事实证明，在某些情况下， SVD 会给我们 不是正确旋转的旋转矩阵。

也就是说，他们也有 围绕旋转轴的反射。

为了确保我们得到正确的旋转， 我们选择右下项为 U 和行列式的乘积 V.

这个数字将是 加一或减一，将抵消任何反射。

一旦我们有了这个，我们所要做的就是 将三个矩阵相乘。

这给了我们最佳的旋转矩阵。

现在，我们有了旋转估计， 最后一步是恢复翻译。

这部分非常简单，只有 涉及旋转的质心 一个点云进入参考框架 另一个，然后取差值 要查找的坐标向量 最好的翻译 对齐两个点云。

另一件重要的事情要考虑， 从安全的角度来看，当我们开始 在后面的模块中讨论传感器融合， 我们应该有多大的信心 ICP算法的输出。

有许多不同的方法可以 估计不确定性或 估计的运动参数的协方差。

一种准确且相对简单的方法 就是在这里使用这个等式。

这个表达式告诉我们协方差如何 估计的运动参数 与协方差有关 使用两个点云中的测量值 的某些二阶导数 最小二乘成本函数。

虽然它的表达式准确且计算速度快， 推导有点棘手 这些二阶导数，当有 一个约束量，如混合中的旋转矩阵。

出于我们的目的，我们通常会手动调音 ICP协方差矩阵给我们可接受的结果。 你现在已经看到了基本的 vanilla 算法 对于迭代最近点法， 但这不是解决问题的唯一方法。

其实这个算法是 只是 ICP 的一种变体，称为点对点 ICP， 它的名字来源于 我们的目标函数或 损失函数最小化距离 对应点对之间。

另一个流行的变种 在非结构化环境中运行良好，例如 城市或室内称为Point-to-plain ICP。

而不是最小化距离 在点对之间， 我们安装了许多飞机 第一个点云，然后最小化距离 在每个点之间 第二朵云和 它在第一朵云中最近的平面。

这些平面可以代表事物 如墙壁或路面。

该算法的挑战性部分是 实际上找出所有飞机的位置。

我们不会详细讨论如何做到这一点， 但您可以查看文档 点对平原ICP 点云库以获取更多信息。

现在，直到现在， 我们一直假设对象 我们的激光雷达看到的是 静止的。

如果他们搬家了怎么办？

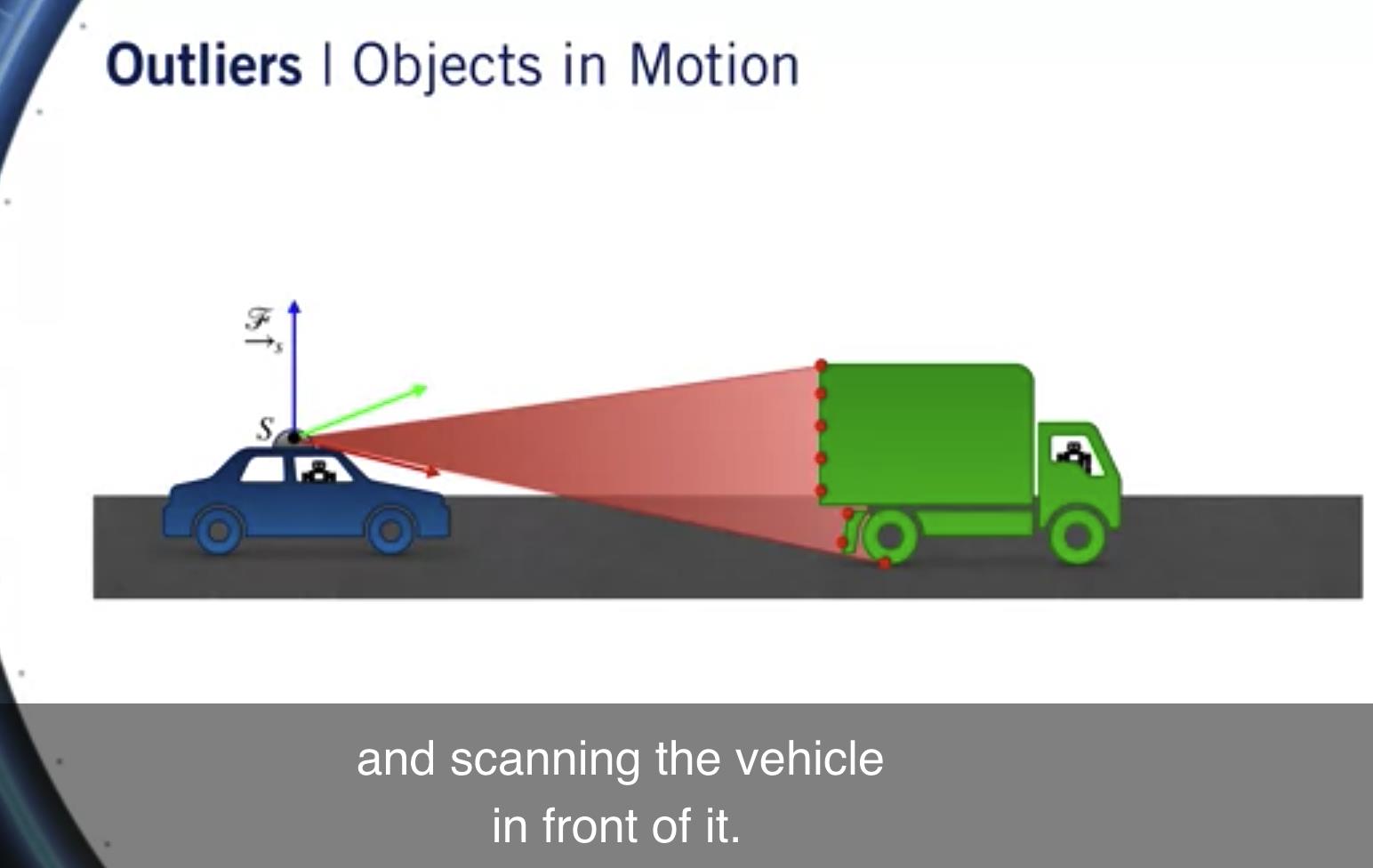
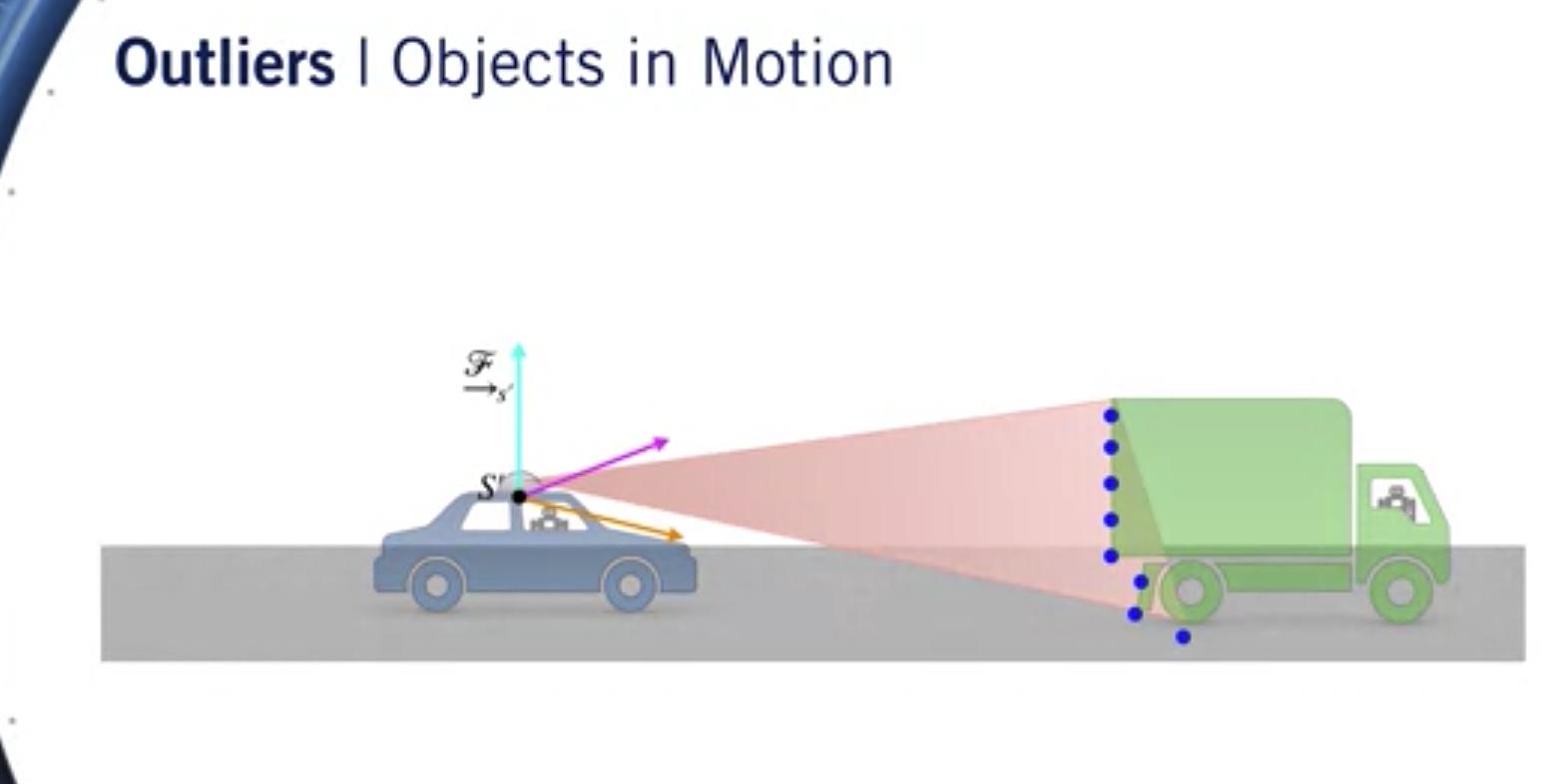
一个常见的例子是，如果我们的汽车正在驶入 在繁忙的高速公路上行驶 并扫描前面的车辆。

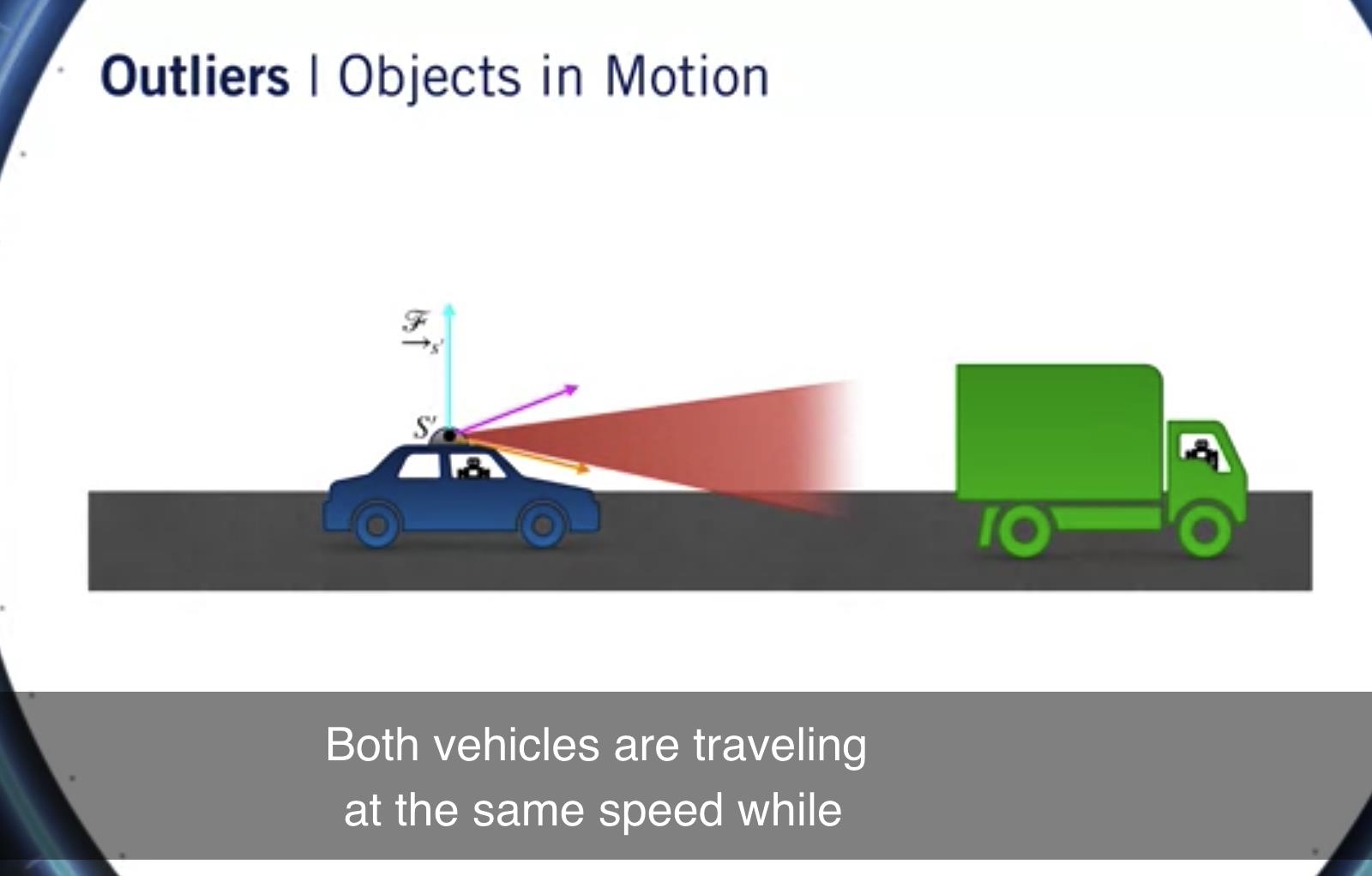
两辆车以相同的速度行驶，而 我们的自动驾驶车开得很开心 收集激光雷达数据点。

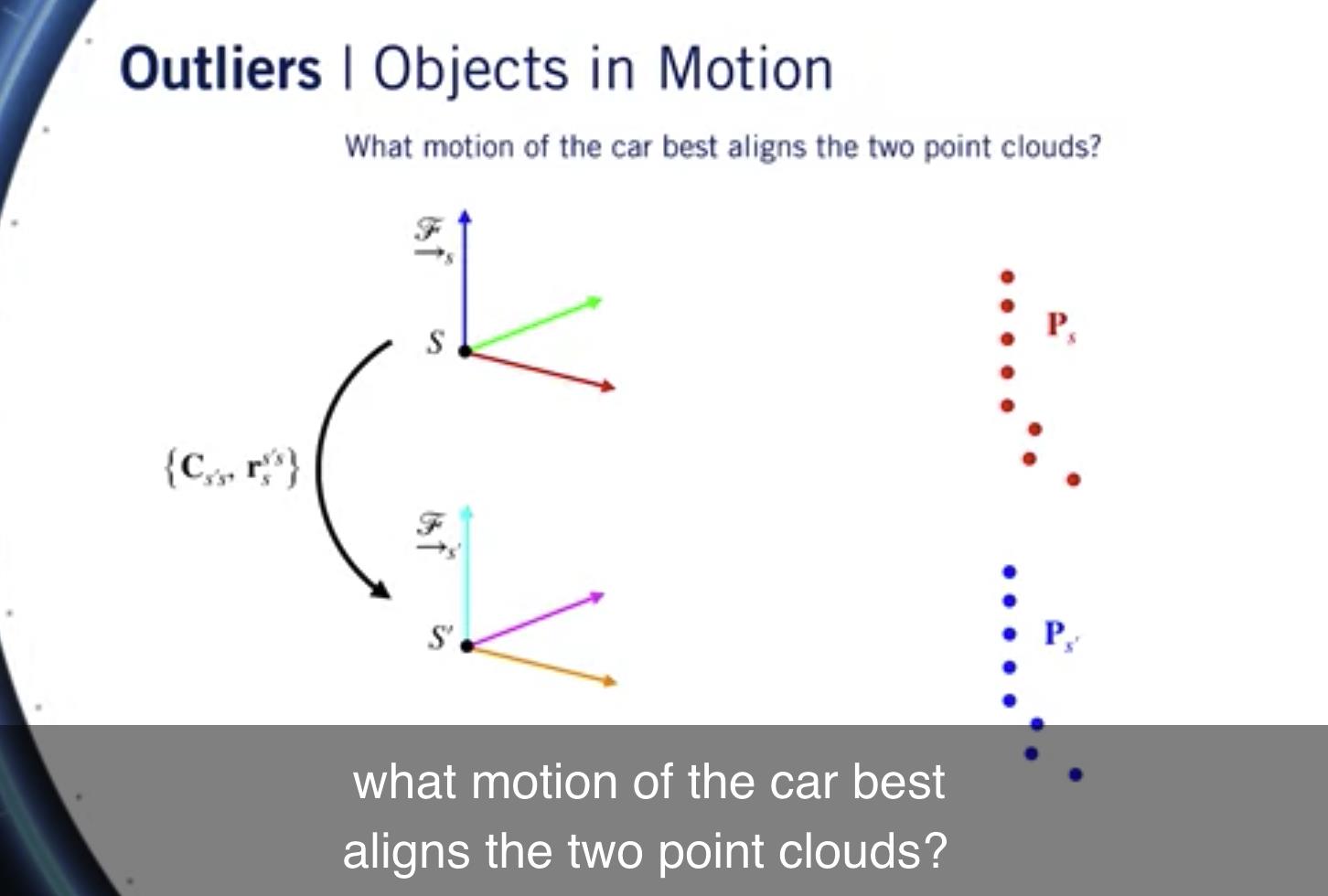
我们再次问自己， 汽车的哪种运动最能对齐两个点云？

我们得到的答案是我们根本没有搬家。

但是，当然，我们确实搬家了， 只是与我们前面的车辆无关。

这显然是一个人为的例子。

实际上，点云还包括 许多静止的物体，如道路， 建筑物和树木。

但天真地在移动的情况下使用 ICP 物体会倾向于拉动我们的运动 估计偏离真实运动。

所以我们需要小心排除或 减轻离群点的影响 违反了我们对静止世界的假设。

一种方法是融合 ICP 运动 GPS 和 INS 估计。

我们将在课程后面讨论如何做到这一点。

另一种选择是识别并忽略移动物体， 我们可以用一些计算机视觉来做 您将在下一课程中学习的技术。

但更简单的处理方法 像这样的异常值是 选择不同的损失函数 对它不太敏感 引起的大错误 异常值比我们的标准平方误差损失。

损失函数的类别 具有此属性的称为 稳健的损失函数或稳健的成本函数， 并且有几个可供选择。

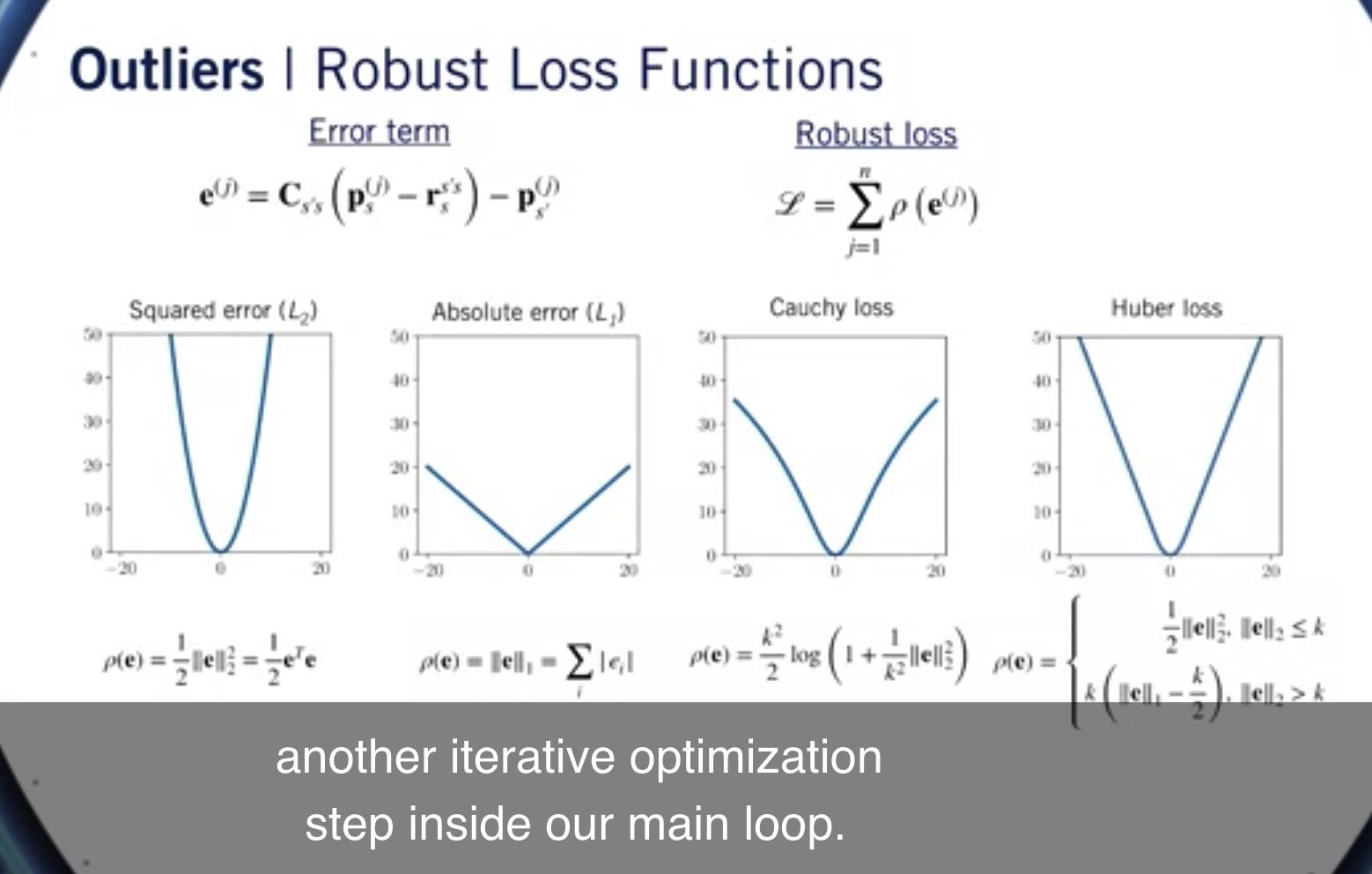
我们可以用数学方法写出来 通过推广我们的最小二乘 损失函数使得贡献 每个误差不仅仅是其大小的平方， 而是一些其他功能 rho。

鲁棒损失函数的一些流行选择 包括绝对误差或 L1 范数， 此处显示的 Cauchy 损失和 Huber 损失。

关键的区别在于 损失函数的斜率 不会随着误差变大而继续增加， 而是保持不变或逐渐减少。

强大的损失函数使 ICP 问题稍微困难一些，因为我们可以 不再导出一个很好的封闭形式解决方案 对于点云对齐步骤， 这意味着我们需要添加 我们主循环中的另一个迭代优化步骤。

然而，好处不能衡量增加的复杂性。

回顾一下，迭代最近点 或者ICP算法是一种判断方法 自动驾驶汽车的运动 对齐来自激光雷达或其他传感器的点云。

ICP通过迭代工作 最小化欧几里得距离 每个点云中的相邻点 这就是算法得名的地方。

移动物体可能是 ICP 的一个问题，因为它们 违反静止世界假设 ICP所基于的。

像这样的异常值测量 可以通过一个数字来缓解 包括鲁棒损失函数在内的技术， 分配较少的权重 比通常的平方误差损失大的误差。

让我们回顾一下我们在本模块中学到的内容。

激光雷达或光检测和 测距是一种测量方式 通过时间观察距离 激光脉冲的飞行。

2D 和 3D 激光雷达传感器可以 扫描汽车周围的大片环境， 以及从返回的点的集合 每次扫描都存储为点云， 可以使用 标准空间操作，例如 如平移、旋转和缩放。

这些操作是重要的组成部分 迭代最近点或 ICP 算法， 这是一种常用的使用技术 激光雷达定位自动驾驶汽车。

在下一个模块中， 我们将讨论一些实际的方面 状态估计并讨论我们如何使用 激光雷达和 ICP 与其他传感器如 IMU 和 GPS 获取 准确可靠的车辆状态估计。

补充阅读：来自激光雷达数据的姿态估计

要了解有关从 LIDAR 数据进行姿态估计的更多信息，请查看以下资源：

• 阅读Timothy D. Barfoot, State Estimation for Robotics (2016)（免费提供）的第 8 章第 1.3 节。

• 阅读有关点集注册和ICP的维基百科文章。

• 检查来自罗马大学“La Sapienza”（现在在苏黎世联邦理工学院）的 Andrea Censi 的一种方法，以产生ICP 协方差的精确封闭形式估计。

• 阅读关于LIDAR 和 Inertial Fusion for Pose Estimation by Non-linear Optimization的研究论文，可在 arXiv 上免费获取。

• 回顾Yang Chen 和 Gerard Medioni (1991)以及Paul Besl 和 Neil McKay (1992)的原始论文，它们首先描述了迭代最近点 (ICP) 算法（的变体）。

参考

https://www.coursera.org/learn/state-estimation-localization-self-driving-cars/lecture/XE9kZ/lesson-3-pose-estimation-from-lidar-data