图神经网络

Posted 2022-02-03 小葵花幼儿园园长

图神经网络

• • • • 为什么用图表示数据
  • 图的知识
  • • • 1. 如何去表示一张图：
      • 2. 图的性质：
  • Graph embedding
  • • • GNN与network embedding（图嵌入）
      • GNN与Graph Kernel

为什么用图表示数据

深度学习在许多领域的成功部分归功于快速发展的计算资源(如GPU)、大训练数据的可用性，以及深度学习从欧几里得数据（如图像、文本和视频）中提取潜在表示的有效性。以图像数据为例，我们可以将图像表示为欧几里得空间中的规则网格。卷积神经网络(CNN)能够利用图像数据的移位不变性、局部连通性和组合性。因此，CNNs可以提取局部有意义的特征，并与整个数据集共享，用于各种图像分析。

虽然深度学习有效地捕获了欧几里得数据的隐藏模式，但数据以图形形式表示的应用越来越多。例如，在电子商务中，以图形为基础的学习系统可以利用用户与产品之间的互动，作出高度准确的推荐；在化学中，分子被建模为图形，他们的生物活性需要被识别为药物发现；在引文网络中，论文通过引文相互链接，需要被分类到不同的组中。

图数据的复杂性给现有的机器学习算法带来了重大挑战。由于图可能是不规则的，一个图可能有大小不等的无序节点，而来自图的节点可能有不同数量的邻居，这导致一些重要的操作(比如卷积)在图像域中容易计算，但很难应用到图域中。此外，现有机器学习算法的一个核心假设是实例是相互独立的。这个假设不再适用于图形数据，因为每个实例（节点）通过各种类型的链接（比如引用、友谊和交互）与其他实例（节点）相关联。

因此，人们对扩展图形数据的深度学习方法越来越感兴趣。受CNNs、RNNs和深度学习带来进展，过去几年来，为了处理复杂的图形数据，对重要操作（如卷积操作等）的新概括和定义得到了迅速的发展。例如，图卷积可以从二维卷积推广。如下图所示，图像可以认为是像素由相邻像素连接的图的一种特殊情况。与2D卷积类似，我们可以通过取节点邻域信息的加权平均值来进行图形卷积。

图的知识

1. 如何去表示一张图：

邻接矩阵的方法

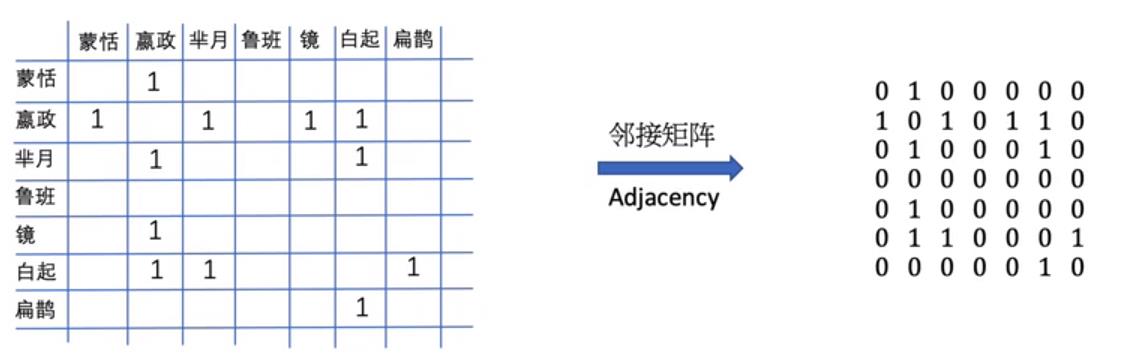
2. 图的性质：

度（degree）

无向图：连接边的数量
有向图：分为出度和入度

连通图、连通分量

对于一个无向图，如果任意节点i能够通过一些边到达节点j，则称之为连通图。

连通分量：无向图G的一个极大连通子图称之为G的一个连通分量（或连通分支）。

度中心性

度中心性 = 某节点的度/（总结点数-1）

中介中心性Betweenness Centrality

连接中心性Closeness

Graph embedding

one-hot向量丢失了节点之间的信息

GNN与network embedding（图嵌入）

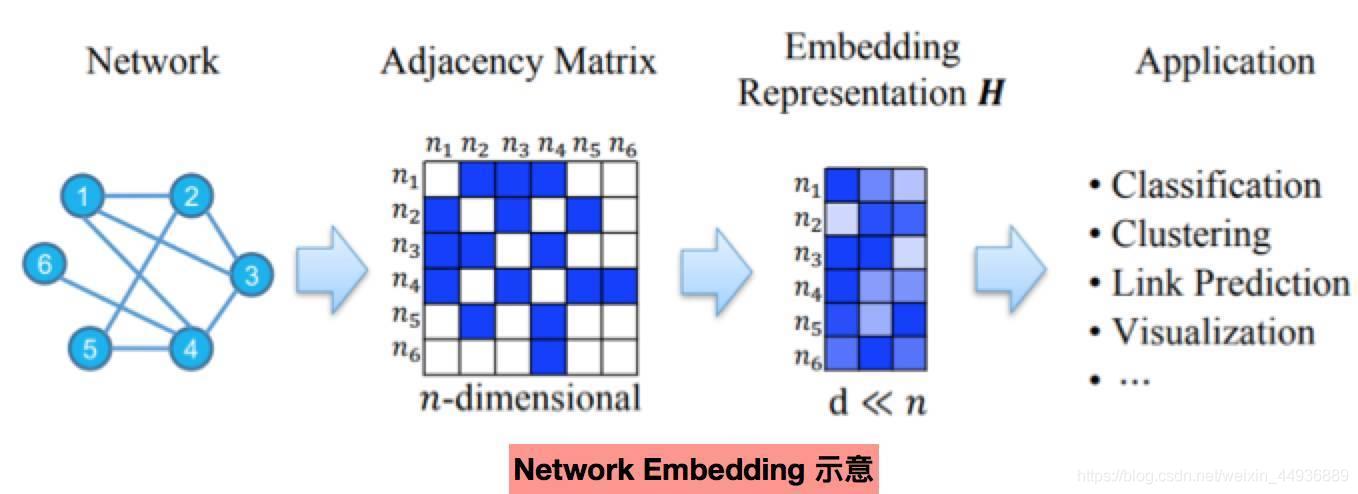
图嵌入：用邻接矩阵来表示图，进行学习得到低微表示，用于后续图像和数据分析任务，如分类、聚类等。

GNN与网络嵌入的主要区别在于，GMM是针对各种任务而设计的一组神经网络模型，而网络嵌入涵盖了针对同一任务的各种方法。因此，GNNs可以通过一个图形自动编码器框架来解决网络嵌入问题。另一方面，网络嵌入还包含其他非深度学习方法，如矩阵分解、随机游走等。

GNN与Graph Kernel

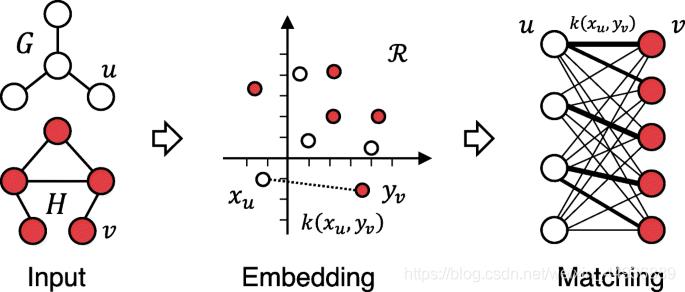
Graph Kernel历来是解决图分类问题的主要技术。这些方法使用一个核函数来度量图对之间的相似性，那么这样基于核的算法（如支持向量机）就可以用于图的监督学习。与GNN类似，Graph Kernel可以通过映射函数将图或节点嵌入到向量空间中。不同的是，这个映射函数是确定性的，而不是可学习的。由于Graph Kernel方法采用两两相似度计算，因此存在较大的计算瓶颈。一方面，GNN直接根据所提取的图表示进行图分类，因此比Graph Kernel方法效率高得多。