B树B+树和B*树

Posted 2022-01-27 Moua

Hash、AVL树、红黑树等结构适用于内查找，当数据量比较大内存中无法加载时，这些数据结构就很难高效的查找。这时，就需要B树来解决。

举个例子：

我们熟悉的mysql数据库是将数据保存在一个个的table中，再将一个个的table保存在硬盘中的。每一个table都是一个二维结构，即行和列。如果业务比较大的时候，一个数据库中可能会存在很多的table，每个table有很多的行和列。在MySQL数据库中每一行是一个表项，表示的是同一事务的信息，如果要在table中查找某个数据时我们可以将每个数据的primary key加载到内存，在使用查找算法进行查找：

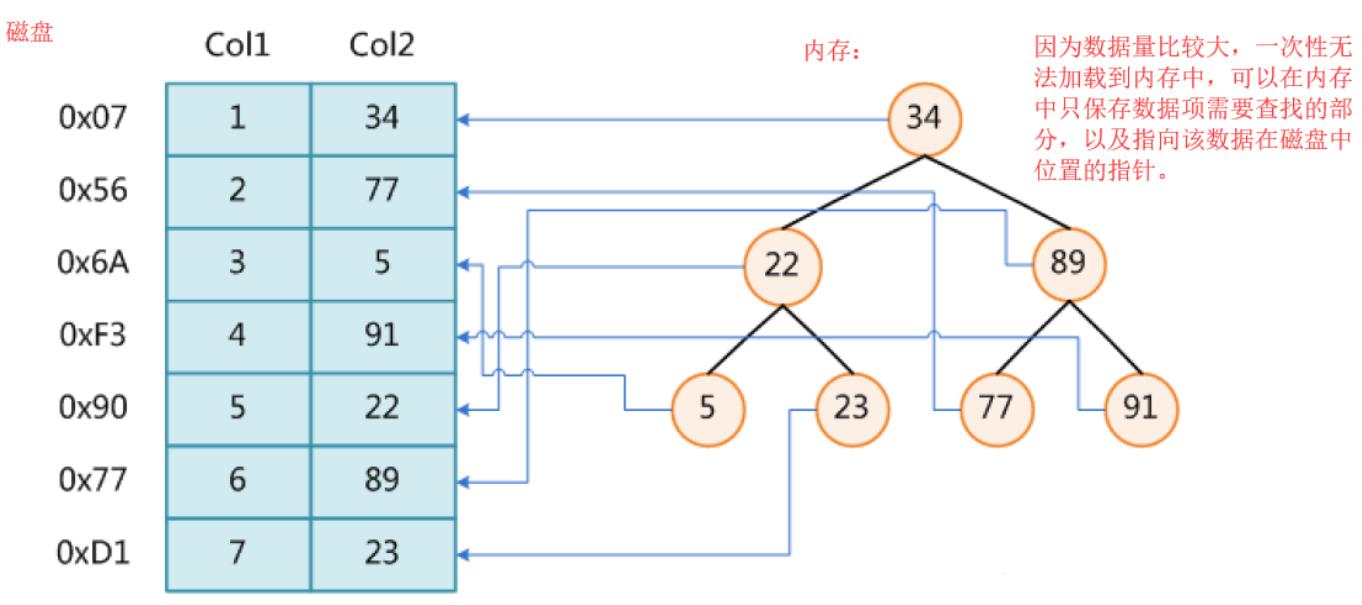
hash：查找的时间复杂度为O(1)，但是数据库中有时候需要进行排序，而hash无法快速的排序。

AVL数/红黑树：查找时间复杂度log(N)，数据有序，看似不错。但是，在磁盘中查找数据，还是要求尽可能减少IO次数提高效率，而AVL数和红黑树的高度太高。

B树、B+树：具有搜索树的特点且树的高度比AVL树和红黑树都要低，堪称完美。

那么，什么是B树呢？

从创建一颗B树来理解B树的性质：

以三叉树为例，插入节点创建B树，节点结构如下：

注意：为了演示方便，采用第二种结构，每次满了后就需要立即进行分裂。 

以序列53, 139, 75, 49, 145, 36, 101构建B树过程如下：

第一步：依次插入53 239 75

注意：插入数据后，每一个节点中的数据是有序的。 

第二步：我们要创建的是M叉的B树（M=3），上图所示节点中有三个键值时，孩子节点的个数为4了，因此需要进行分裂，分裂规则如下：

• 找到需要分裂节点的中间位置
• 创建两个新节点，将节点中的一半数据搬到新节点中，该节点作为原来节点的兄弟节点
• 将中间节点搬到另一个新的节点，该新节点作为另外两个的父节点

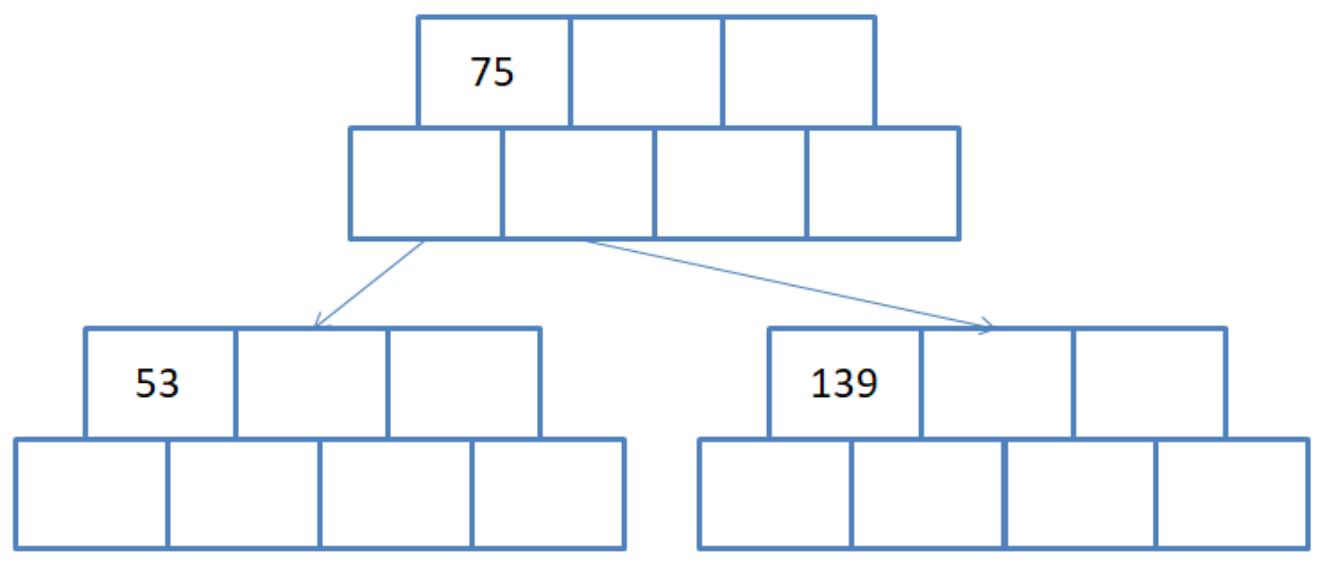
第三步：插入49 145...为了方便后序查找，每个节点中的数据都是有序的，插入后如下：

注意：找到插入位置后，按照插入排序的思想进行插入。插入完成后在检测是否满足B树性质。

第四步：插入36 101，并进行分裂

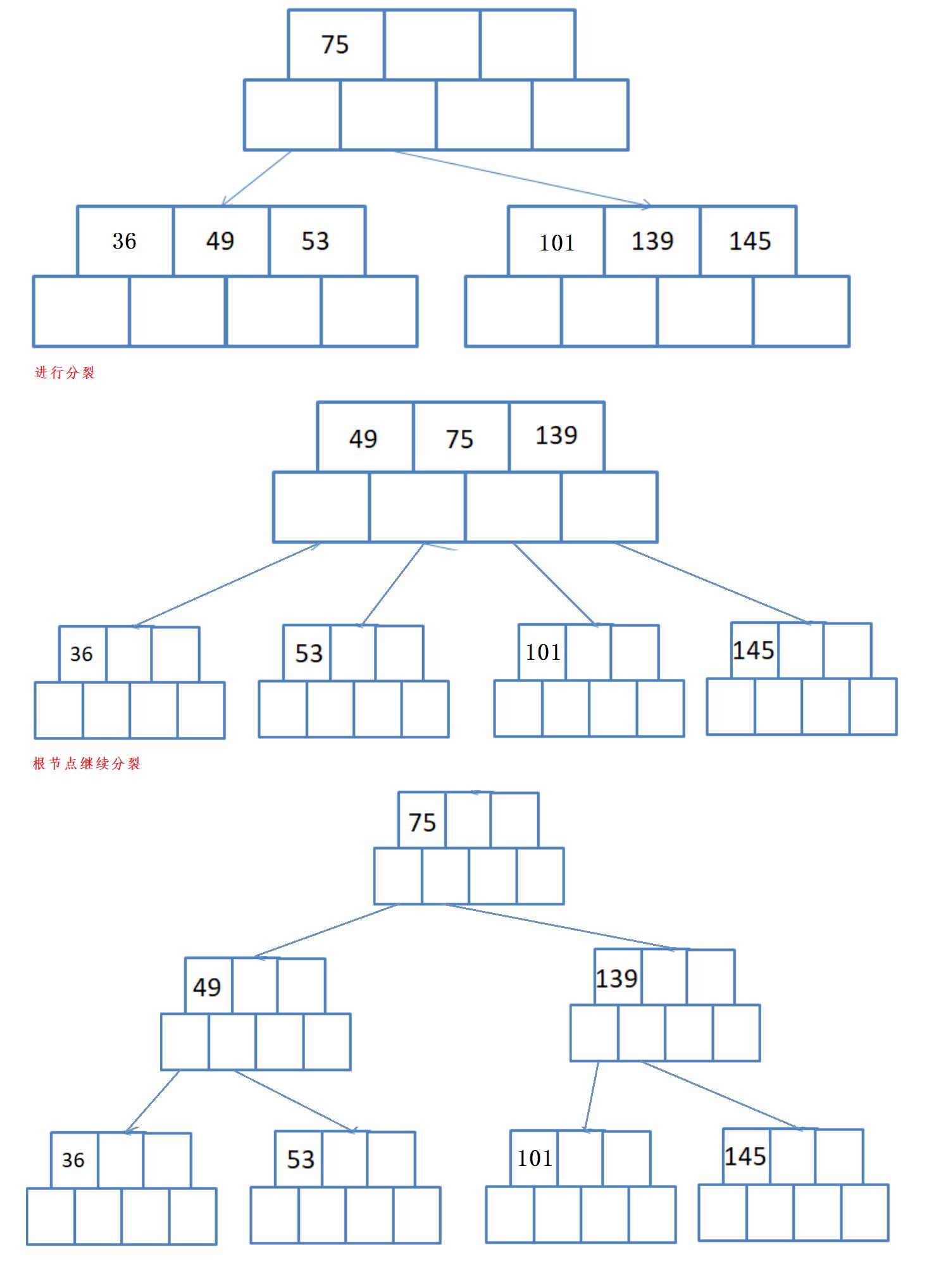
插入过程总结：

• 如果树为空，直接插入新节点，插入的新节点为树的根节点
• 树为非空，找待插入元素的位置（可以向AVL树那样找，因为B树也满足根节点的左孩子比他小右孩子比他大）。
• 按照插入排序的思想，将待插入节点插入到节点中（注意：需要保证插入后数据有序）。
• 检测是否需要进行分裂（M叉B树最多有M个孩子节点，由此可以推出最多有M-1个键值）。

分裂过程总结：

• 申请两个新节点，一个作为父节点，一个作为兄弟节点。
• 找到待分裂节点的中间节点
• 中间节点拷贝到新节点，该新节点作为B树的新的根节点。
• 右边一半数据拷贝到另一个新的节点，该新节点作为原来节点的兄弟节点。

根据插入过程总结B树的性质： 

• 根节点至少有两个孩子节点：根节点一定是由一个节点分裂而来的，一个节点分裂后有三部分，即两个孩子节点一个父节点，父节点必然至少有两个孩子节点。
• 每个非根节点的节点个数为M/2~M个：M叉树每个节点最多有M个孩子，当键值数为M时需要进行分裂，此时孩子节点最少为：M/2。
• 每个非根节点的键值数为M/2-1~M-1：可以理解成M-1个节点可以将一个线段分成M段。在这里M-1个键值刚好有M个孩子节点。
• 所有叶子节点都在同一层
• 每个节点中的键值都是有序的，且每个节点中键值的个数比孩子节点的个数总是少1个。

性能分析：

对于一颗有N个节点的M叉，需要进行log(M-1)N ~ log(M/2-1)N次比较可以定位到节点，定位到节点后在进行二分查找，log(M)就可以找到具体节点。

B+树

B+树是B树的变形，也是一颗多叉搜索树：

• 根节点至少有两个孩子节点
• 每个节点的孩子节点个数和键值个数相等（不同于B树）
• 它的每个节点不存具体的值，每个节点存储的是到某一区间的路径
• 所有关键字都存储在叶子节点中，为每一个叶子节点增加一个指针将所有叶子节点链接在一起。

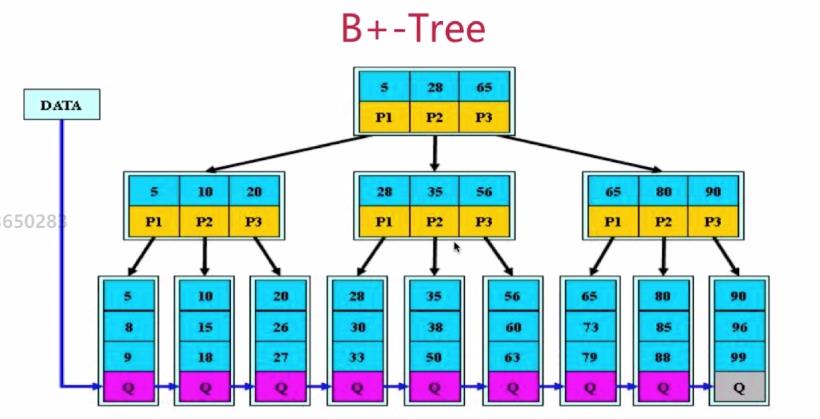
B*树

 B*树是B+树的变形，在非根和非叶子节点增加一个指向兄弟节点的指针：