如何获得扬声器完美的单位冲激响应？

Posted 2023-03-09 卓晴

• 扬声器的单位冲激响应信号建模

扬声器的单位冲激响应

 

01 单位冲激响应

---

一、前言

  在短片“ 扬声器敲击信号 ”中，使用改锥敲击的方法来获得扬声器的单位冲激响应信号。 但由于受的敲击的影响， 所获得的单位冲激响应波形并不完美。 敲击不同的部位和力度，所采集到的音圈电压波形相差很大。 例如这是另外一次敲击对应的波形。 这是小心翼翼敲击扬声器中心所产生的衰减振荡的信号波形。  看似比较完美，但实际上前面5毫秒的波形是敲击所造成的强迫相应。 下面准备通过使用电源激励的方式， 来获得扬声器比较完美的单位冲激响应信号。

二、直流电数据

1、测量方法

  对于待测动圈式扬声器， 使用一台直流稳压电源， 输出直流3V电压施加在扬声器上。 利用开关控制电流的通断。 一开始的时候通电， 扬声器流过一个直流电流。 将开关断开， 电流出现一个阶跃变化。 利用示波器测量测量扬声器震动的电压信号。

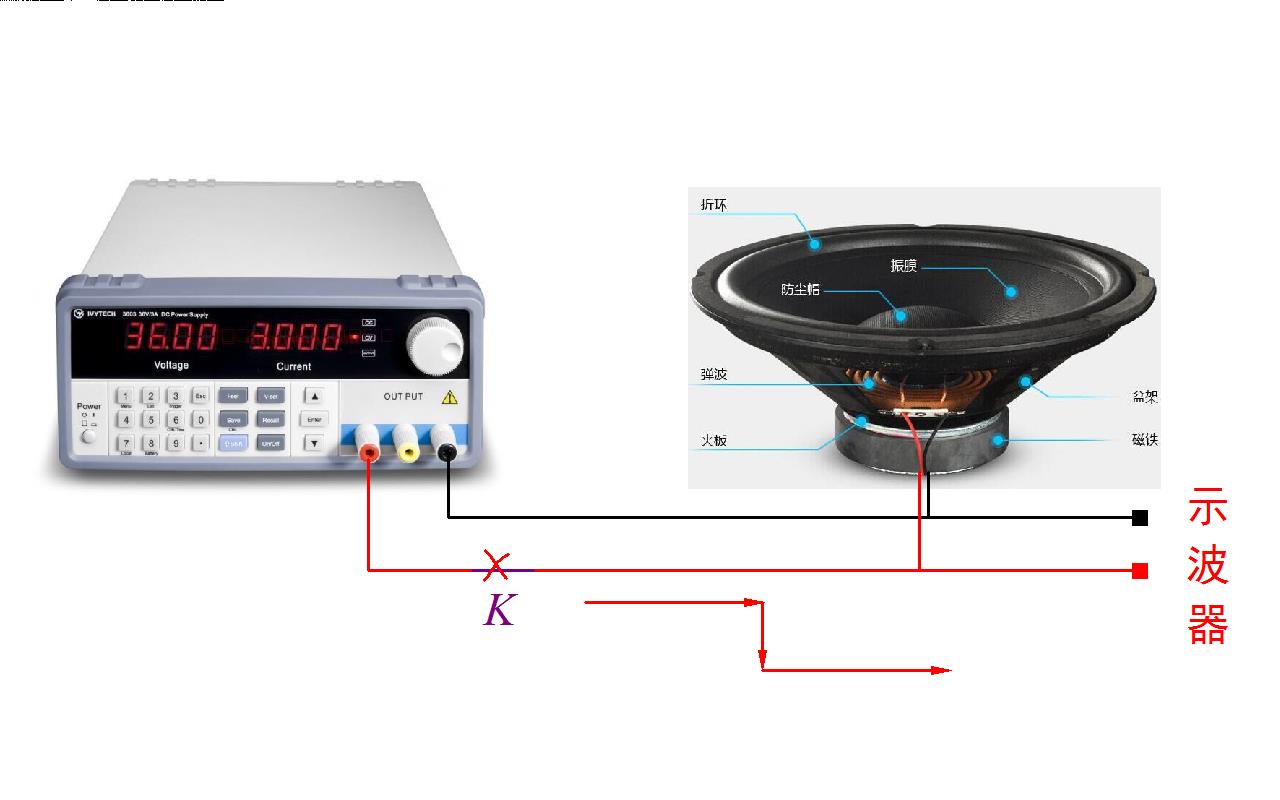
  由于扬声器音频线圈输出电压正比于运动速度， 也就是正比于线圈位置变量的导数。 阶跃电压激励后的震动信号与振膜的冲激响应是相同的。 由于没有敲击过程，所以可以获得比较完美的单位冲激响应。

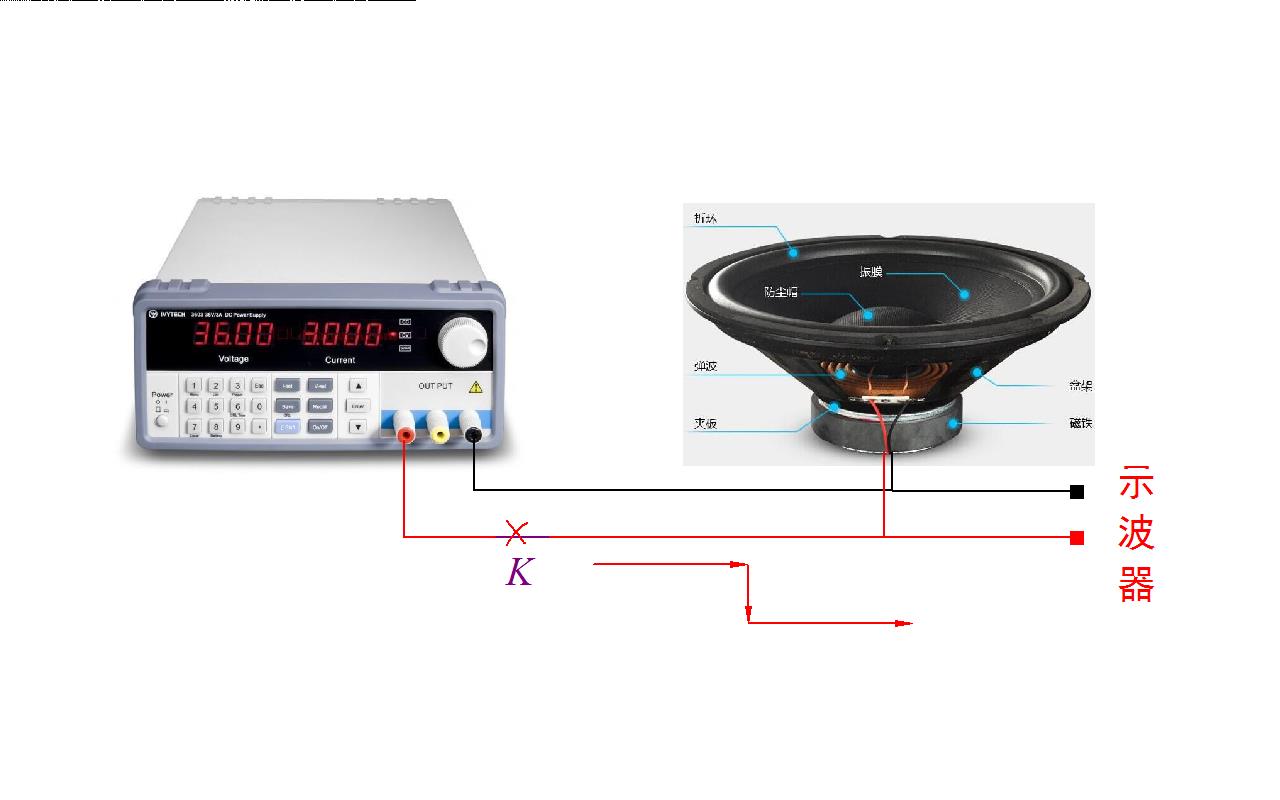
  下面展示一下测量的实际过程。  

（1）读取数据波形程序

from headm import *
from tsmodule.tsvisa        import *
mso24open()
x,y = mso24read(1)
tspsave('wave1', x=x, y=y)
plt.plot(x, y)
plt.xlabel("Time(s)")
plt.ylabel("Voltage(V)")
plt.grid(True)
plt.tight_layout()
plt.show()

（2）曲线拟合程序

from headm import *
from scipy.optimize        import curve_fit
x, y = tspload('wave1', 'x', 'y')
printf(len(x), len(y))
AVERAGE_NUM = 50
DATA_LENGTH = len(x)//AVERAGE_NUM
xx = array([sum(x[i*AVERAGE_NUM:i*AVERAGE_NUM+AVERAGE_NUM])/AVERAGE_NUM*1e3 for i in range(DATA_LENGTH)])
yy = array([sum(y[i*AVERAGE_NUM:i*AVERAGE_NUM+AVERAGE_NUM])/AVERAGE_NUM for i in range(DATA_LENGTH)])
c = where(xx>0.5)
xxx = xx[c]/1000
yyy = yy[c]
tspsave('wave11', xxx=xxx, yyy=yyy)
'''
plt.plot(xxx, yyy)
plt.xlabel("Time(s)")
plt.ylabel("Voltage(V)")
plt.grid(True)
plt.tight_layout()
plt.show()
'''
def fun(x,a,b,c,d,e):
    return a*exp(-b*x)*sin(c*x+d)+e
param = (1, 50, 2*pi*150, 0, 0)
param, conv = curve_fit(fun, xxx, yyy, p0=param)
printf(param)
ysim = fun(xxx, *param)
plt.plot(xxx, yyy, linewidth=3, label='Origin')
plt.plot(xxx, ysim, label='Fit')
plt.xlabel("Time(s)")
plt.ylabel("Voltage(V)")
plt.grid(True)
plt.legend(loc="upper right")
plt.tight_layout()
plt.show()

2、测量结果

  这是测量得到的一次震动结果，看起来非常完美。 这是利用之前实验的Python程序， 获得该指数衰减振荡波形参数。 其中包括有五个参数。 参数C对应着振荡角频率。 可以计算出扬声器纸盆自由振荡频率为158.3赫兹。 这个频率更加接近于实际波形过零点对应的振荡频率。

▲ 图1.3.1 采集到的一次数据波形

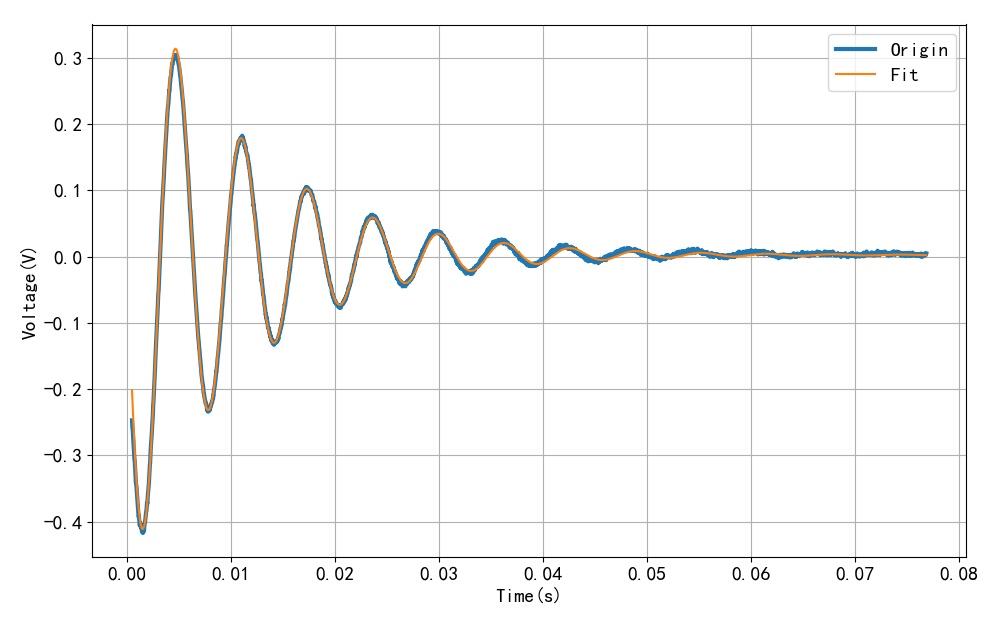
▲ 对滤波后的波形进行滤波拟合后的结果

$$y\left(t\right)=a\cdot \exp \left(-bt\right)\cdot \sin \left(c\cdot t+d\right)+e$$

a=-4.76475410e-01 
b=8.99951149e+01
c=9.94697547e+02
d=-4.15701647e-02
e=2.45613284e-03

3、大扬声器测量结果

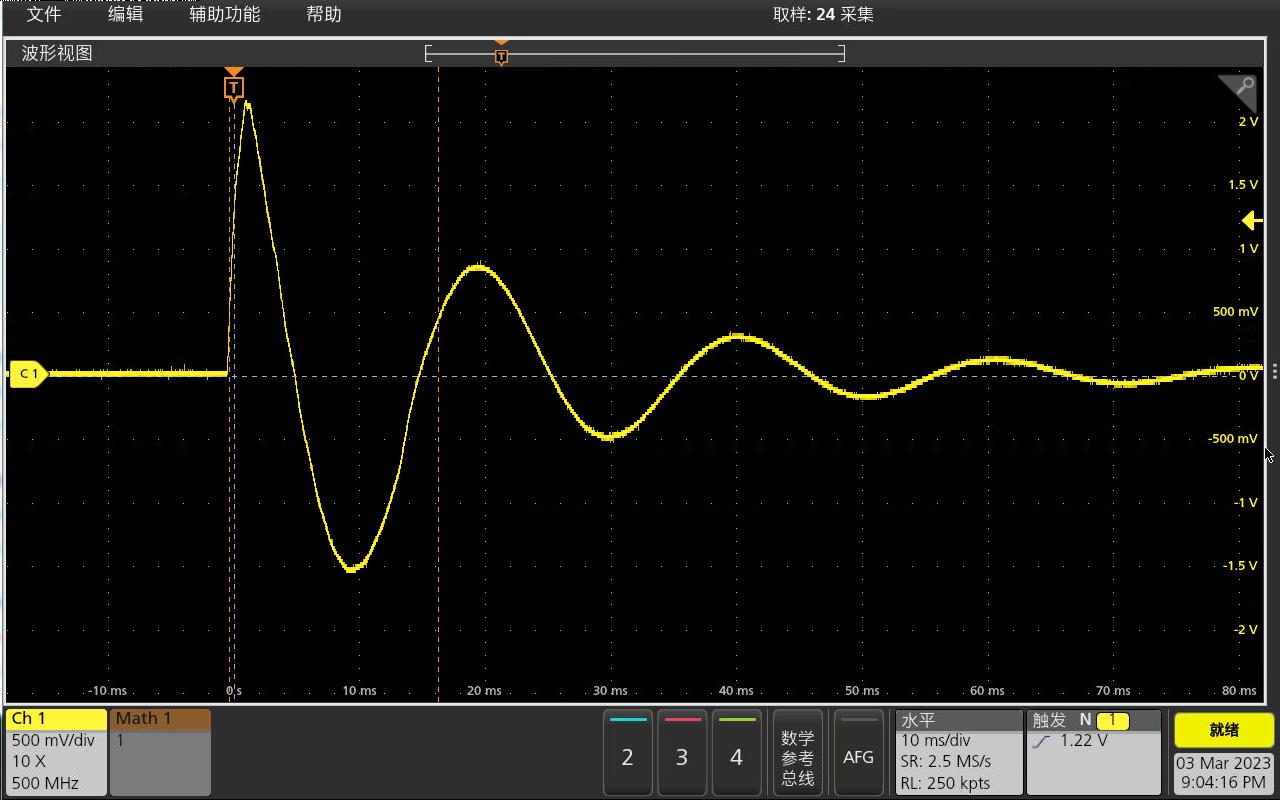
  下面更换一个大型的扬声器， 同样利用阶跃电压测量得到它对应的单位冲激响应。 利用联网的MSO24示波器， 读取它测量得到的电压波形。 利用函数拟合方法， 可以获得该信号衰减振荡参数。 可以看到它所对应的振荡角频率比小型扬声器小了三倍左右。

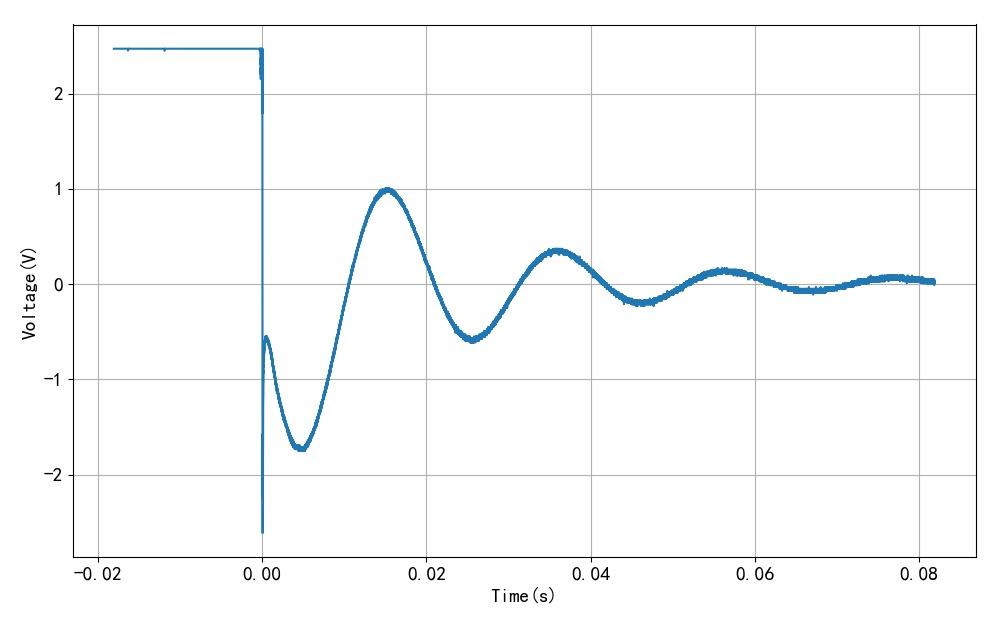
▲ 图1.3.3 大扬声器测量结果

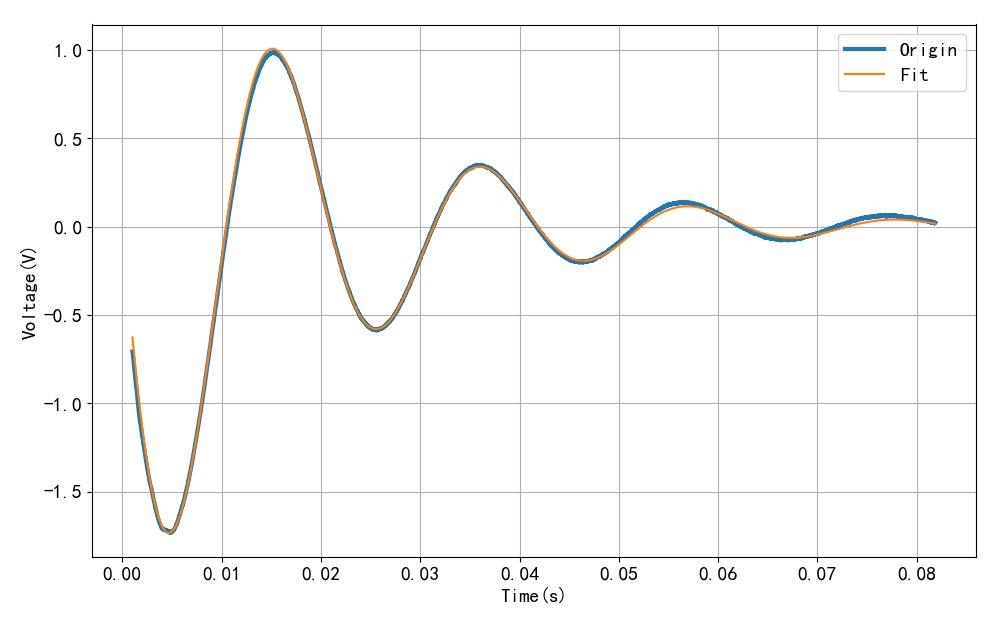
▲ 图1.3.4 拟合数据结果

  衰减振荡波形函数拟合后的参数为：

a=2.24774883e+00 
b=5.22678402e+01 
c=3.00658559e+02 
d=3.13728636e+00
e=2.69832694e-03

三、敲击大喇叭

  为了对比， 下面通过敲击测量扬声器的冲击信号。可以看到所能够获得的波形不太完整。 这是另外一次敲击的波形， 效果有所改进。 尽量使得敲击短促，可以减少敲击的影响。 下面多试几次， 争取尽可能获得比较完美的衰减振荡波形。

▲ 图1.4.1 敲击扬声器所获得到波形
  这是一次比较完美的敲击波形。 可以看到前面部分的波形明显受到敲击的影响， 不太像自由振动的样子。 后面这部分则呈现出比较光滑的自由二阶震动的波形模样。 通过曲线拟合， 整体效果还是不错的。 这说明大扬声器使用直接敲击也可以同样获得比较精确的单位冲激响应信号。

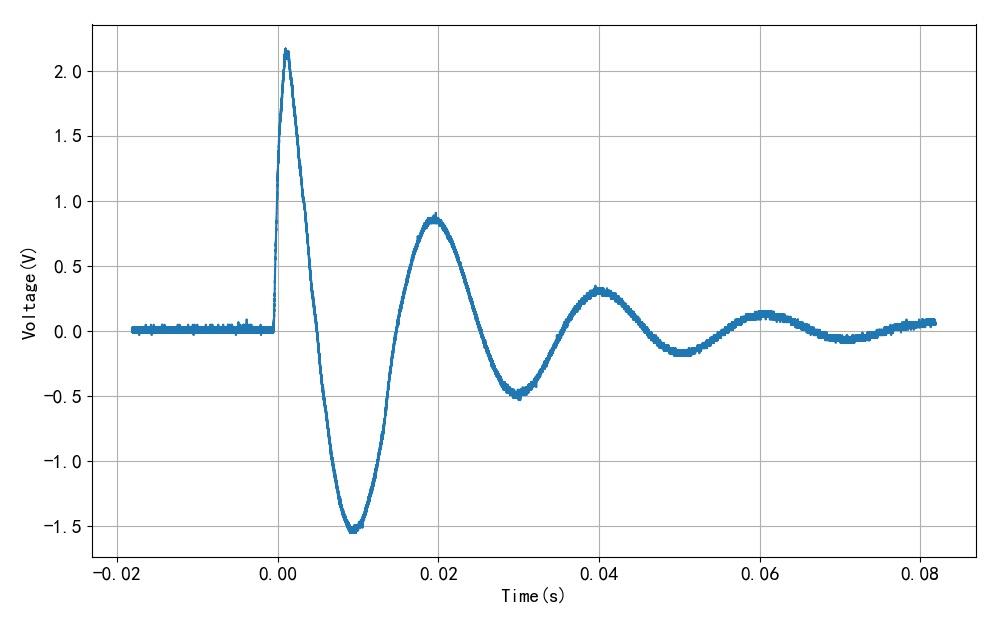
▲ 图1.4.2 敲击大喇叭对应的波形

▲ 图1.4.3 拟合后的曲线

 

※ 总  结 ※

---

  本文通过给扬声器施加阶跃电压， 获得了扬声器的单位冲激响应。 这种方法不受敲击的影响，所得到的单位冲激响应接近于完美。

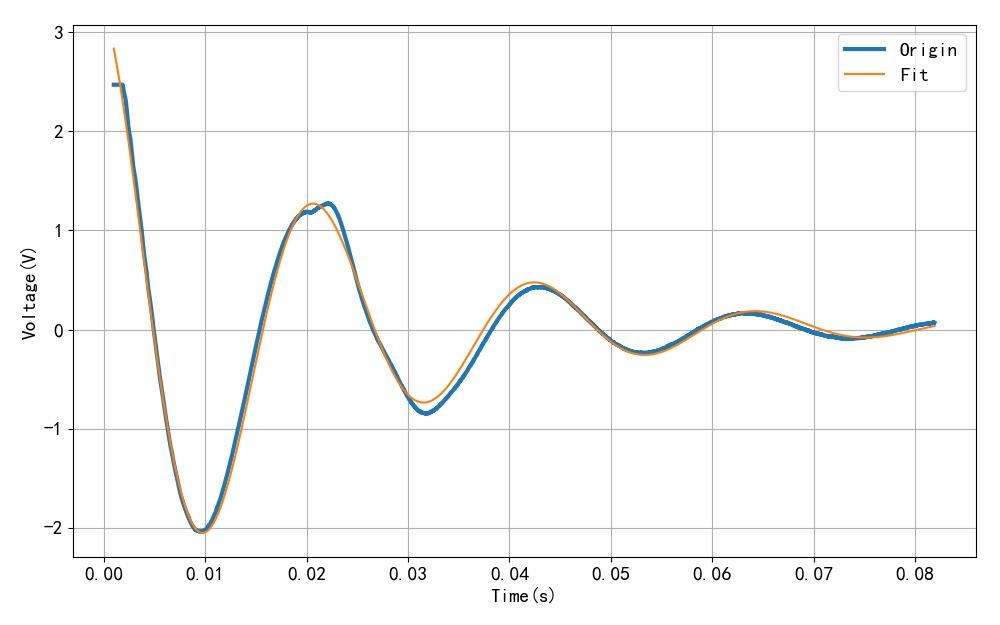
▲ 图2.1 大型扬声器敲击后的波形以及拟合参数

---

■ 相关文献链接:

• 扬声器的单位冲激响应信号建模

● 相关图表链接:

• 图1.3.1 采集到的一次数据波形
• 对滤波后的波形进行滤波拟合后的结果
• 图1.3.3 大扬声器测量结果
• 图1.3.4 拟合数据结果
• 图1.4.1 敲击扬声器所获得到波形
• 图1.4.2 敲击大喇叭对应的波形
• 图1.4.3 拟合后的曲线
• 图2.1 大型扬声器敲击后的波形以及拟合参数