论文笔记:Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文笔记:Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks相关的知识,希望对你有一定的参考价值。
1 Intro
- 多元时间序列通常假定变量之间是有关联的
- 每个变量不仅仅由自己的历史信息,还由其他变量决定
- 但现有方法并不能很有效地挖掘变量之间的关系
- 统计模型(VAR、高斯过程GP等)
- 假设变量之间有着线性依赖关系
- 统计模型的复杂度是变量规模的二次方
- 同时变量规模大的时候,会导致过拟合
- 深度学习模型(LSTNet,TPA-LSTM等)
- 论文笔记:Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks_UQI-LIUWJ的博客-CSDN博客
- 他们虽然也在一定程度上建模了变量之间的关系(使用卷积、使用attention等),但并没有显示地建模变量间的关系
- ——>缺乏一定的可解释性
- 基于图的模型
- GNN可以使得图中的每个点能看到他邻居的信息
- 目前的模型会将时间序列+已知的图结构作为输入,进行预测以得到输出
- 但是这类方法会有如下的挑战
- 未知的图结构
- 现有的基于graph的方法依赖于实现已经确定的图结构,但是很多时候多元时间序列并没有显式的图结构
- 图结构学习
- 有的问题中,即使图结构是知道的,但是已知的图结构大多是基于邻接矩阵的,这并不是一个最佳的表示时间序列各变量之间关系的方法
- ——>图结构应该在训练的时候被更新。
- 未知的图结构
- 统计模型(VAR、高斯过程GP等)
- 这篇论文希望解决上述的两个基于图的模型中的挑战

- 挑战1——>论文提出了一种新的图结构学习方法,能够基于数据提取出稀疏邻接矩阵
- 挑战2——>在端到端的模型中,同时建模时间序列、学习图结构
2 问题定义
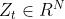 ——t时刻的多元时间序列 value值
——t时刻的多元时间序列 value值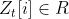 ——t时刻第i个变量的value值
——t时刻第i个变量的value值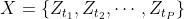
- 目前是预测
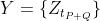 (单步),或者
(单步),或者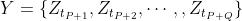 (多步)
(多步) - 如果有D-1个辅助变量的话,可以合成新的输入
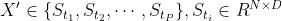
3 模型

3.1 图学习
- 使用如下方法学习单向图
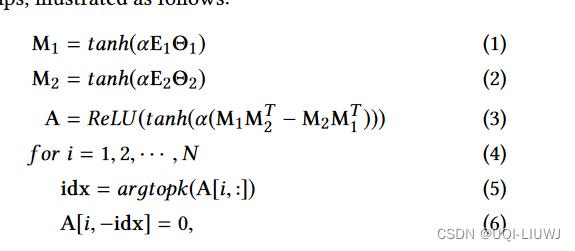
- E1,E2是随机初始化的点embedding,他们会在训练的过程中不断更新
- Θ1,Θ2是模型的参数
- α是一个超参数,控制激活函数的饱和度
- 公式3 决定了模型是单向图,不对称的:如果Auv是正的,那么它的对角元素Avu肯定是0
- 公式5~6 只选最近的k个邻居,其他的边权重设置为0
- -idx我理解是不在idx中的索引部分
3.2 图卷积模块
- 由两个mix-hop propagation 模块组成,分别表示流入和流出点的信息
- 网络的流入信息是由两个mix-hop 模块的输出加和得到的
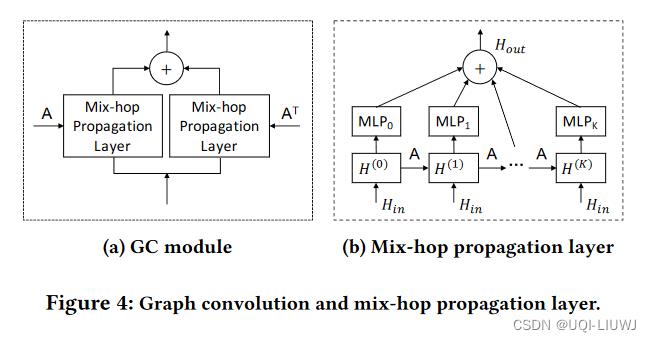
- 网络的流入信息是由两个mix-hop 模块的输出加和得到的
3.2.1 Mix-hop Propagation Layer
-
包含两步
-
信息传递
-

-
其中β是一个超参数,控制保留点原始数据的比例
- Hin是从上一层得到的隐藏状态
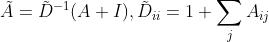
- 递归地传递点信息
-
- 使用β的原因是,防止GNN过渡平滑(所有的点都平滑收敛到很相近的状态)
- ——>保留一部分点的原始状态
- ——>使得propagation能同时保持本地性&探索点的邻居
-
-
信息选择
-
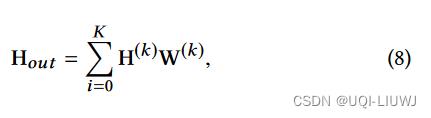
- Hout是当前层的输出
- K表示propagation的深度
- 参数矩阵W是用来选择需要的
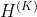
-
-
3.2.2 我的疑问(欢迎评论区赐教)
- 我不太理解这边为什那么需要A和A^T的mix-hop
- 首先,如果A表示流入的information,A^T表示流出的information,那么净流入的information应该是A的mix-hop输出减去A^T的mix-hop输出才对
- 其实,同时使用A和A^T来进行propagation,可以近似等价于使用A+A^T来进行propagation,那就又变成了一个bi-direction的邻接矩阵了。但论文说他需要的是uni-direction的邻接矩阵,有点矛盾?
3.3 时间卷积模块

- 使用空洞卷积,以获取high-level的时间特征
- 一个时间卷积模块也是由两个dilated inception layer组成的,其中右边的是一个门空(激活函数是sigmoid)
3.4 训练方法
- 如果图很大的话,邻接矩阵的搭建将会很占内存——>一个瓶颈
- 论文在每个迭代过程中,随机将点分成若干个组,让算法对每个子图学习图结构
- 比如我们分成了s个组,那么时间和空间复杂度将从O(N^2)降至

- 比如我们分成了s个组,那么时间和空间复杂度将从O(N^2)降至
4 实验部分
4.1 数据集
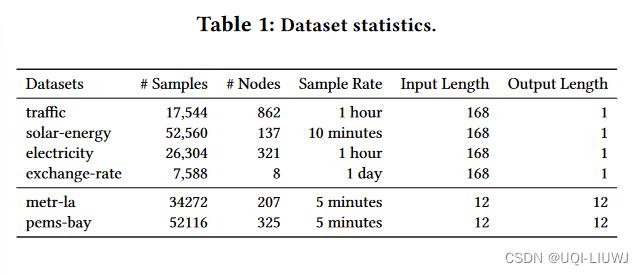
4.2 实验结果

4.3 构建的图(实例)

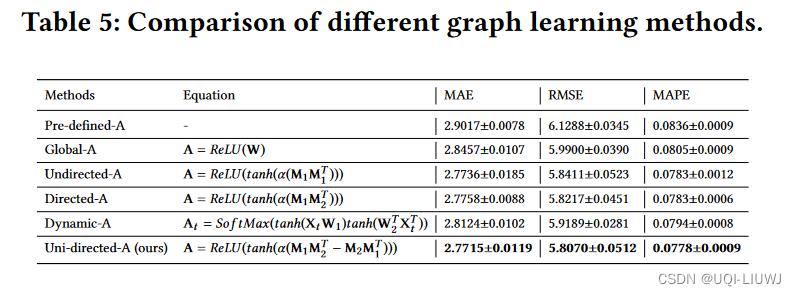
4.4 不同graph learning方法汇总
以上是关于论文笔记:Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks的主要内容,如果未能解决你的问题,请参考以下文章