Unity3D空间和变换

Posted 2023-03-04 little_fat_sheep

1 空间

1.1 左右手坐标系及其法则

1.1.1 左右手坐标系

左手坐标系与右手坐标系

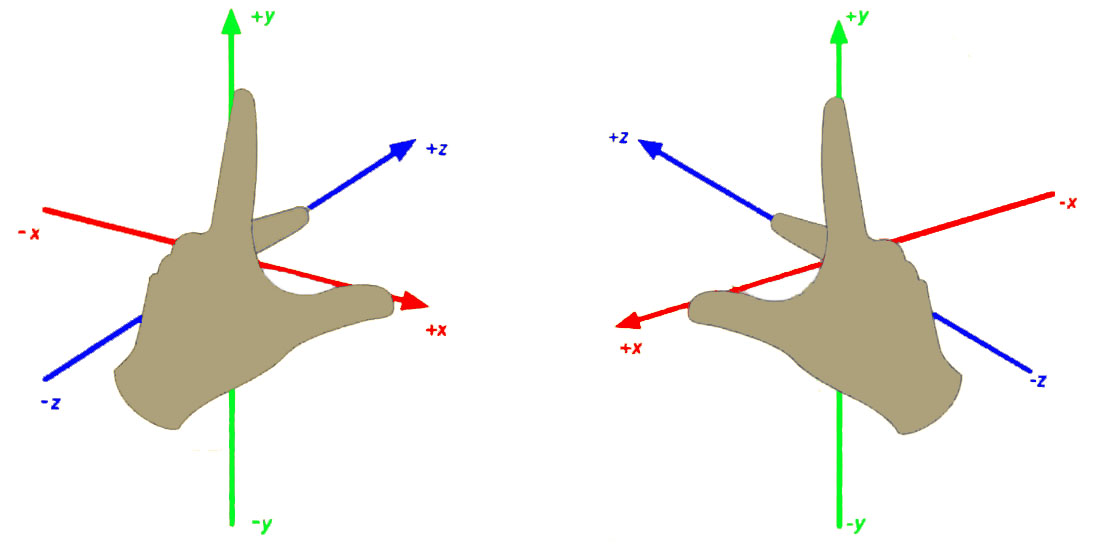
        Unity 局部空间、世界空间、裁剪空间、屏幕空间都采用左手坐标系，只有观察空间采用右手坐标系。

        左右手坐标系除了坐标系朝向（旋向性）不同，还存在以下差异： 

• 左手坐标系下旋转正方向的定义遵循左手法则，右手坐标系下旋转正方向的定义遵循右手法则；
• 左手坐标系下向量叉乘遵循左手法则，右手坐标系下向量叉乘遵循右手法则。

1.1.2 左右手法则

        左手坐标系和右手坐标系下旋转正方形定义： 

左手旋转法则与右手旋转法则

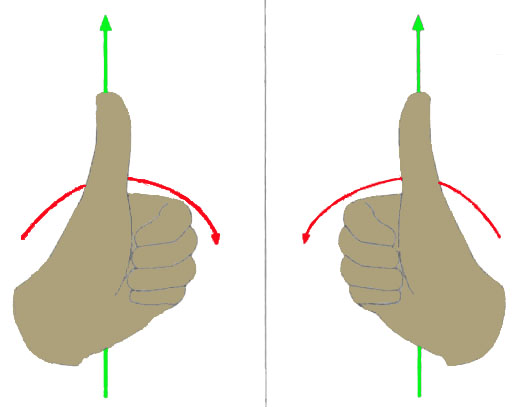
         左手坐标系和右手坐标系下向量叉乘方向定义： 

左手叉乘法则与右手叉乘法则

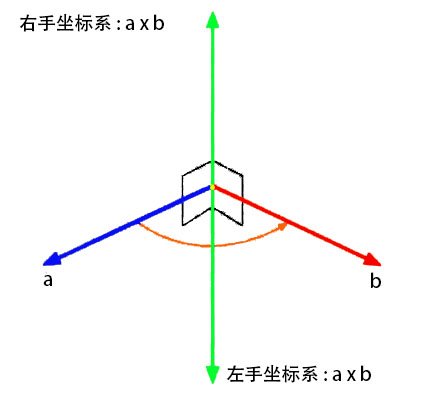
1.2 四维空间

        在三维空间中，将向量 u 变换到向量 v，如果该变换是一个线性变换，一般可以使用一个不依赖于 u、v 的 3x3 的矩阵描述，即 A·u=v，其中 A 是描述该线性变换的变换矩阵。但是，并不是所有线性变换都能使用 3x3 矩阵描述，如：平移变换和对称变换，对于这些变换，需要将空间扩展到四维空间中，再使用 4x4 矩阵描述。

        Unity 模型变换主要有平移、旋转、缩放、对称，其中旋转和缩放变换可以使用 3x3 矩阵描述，平移和对称变换必须使用 4x4 矩阵描述，为了统一描述这些变换，将三维空间扩展到四维空间中，扩展方法如下：

• 三维空间中的坐标原点 [0, 0, 0]' 映射到四维空间中的 [0, 0, 0, 1]' 点；
• 三维空间中的 x、y、z 轴正方向单位向量 [1, 0, 0]'、[0, 1, 0]'、[0, 0, 1]' 分别映射到四维空间中的 [1, 0, 0, 0]'、 [0, 1, 0, 0]'、 [0, 0, 1, 0]' 向量；
• 新添加的 w 轴 正方向单位向量为 [0, 0, 0, 1]'。

        注意：三维空间中的原点 [0, 0, 0]' 并没有映射到四维空间中的原点 [0, 0, 0, 0]，而是映射到 [0, 0, 0, 1]。

         由以上空间映射关系可知：

• 三维空间中的任意点 [x, y, z]'，对应的四维空间坐标为：[x, y, z, 1]'；
• 三维空间中的任意向量 [x, y, z]'，对应的四维空间坐标为：[x, y, z, 0]'。

1.3 Unity 空间

1.3.1 Unity 空间变换过程

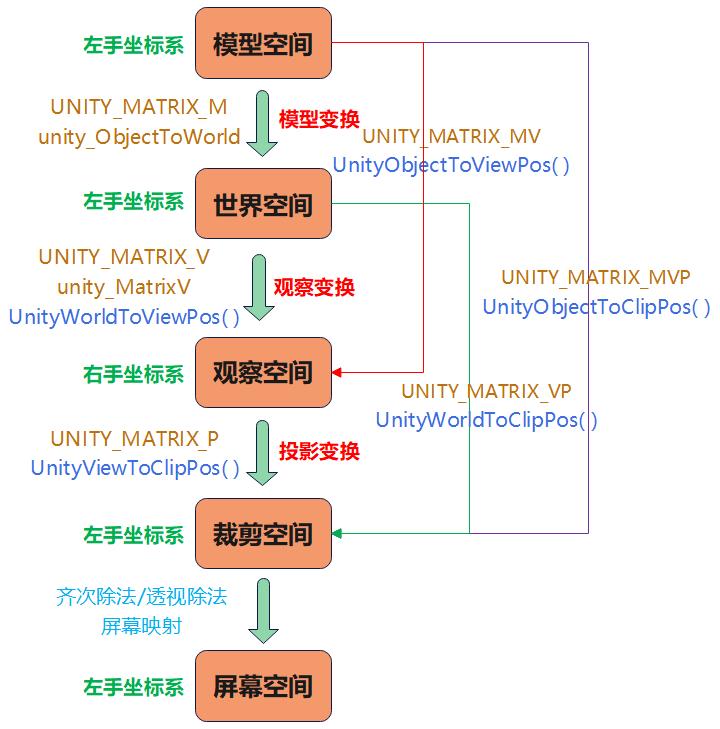
• 从模型空间到裁剪空间的变换过程在顶点着色器中完成，顶点着色器输入模型局部坐标，输出裁剪空间中的坐标； 
• 从裁剪空间到屏幕空间的变换过程由系统控制，用户不能控制该阶段变换。

1.3.2 Unity 空间变换示意图

模型空间、世界空间、 观察空间

观察空间

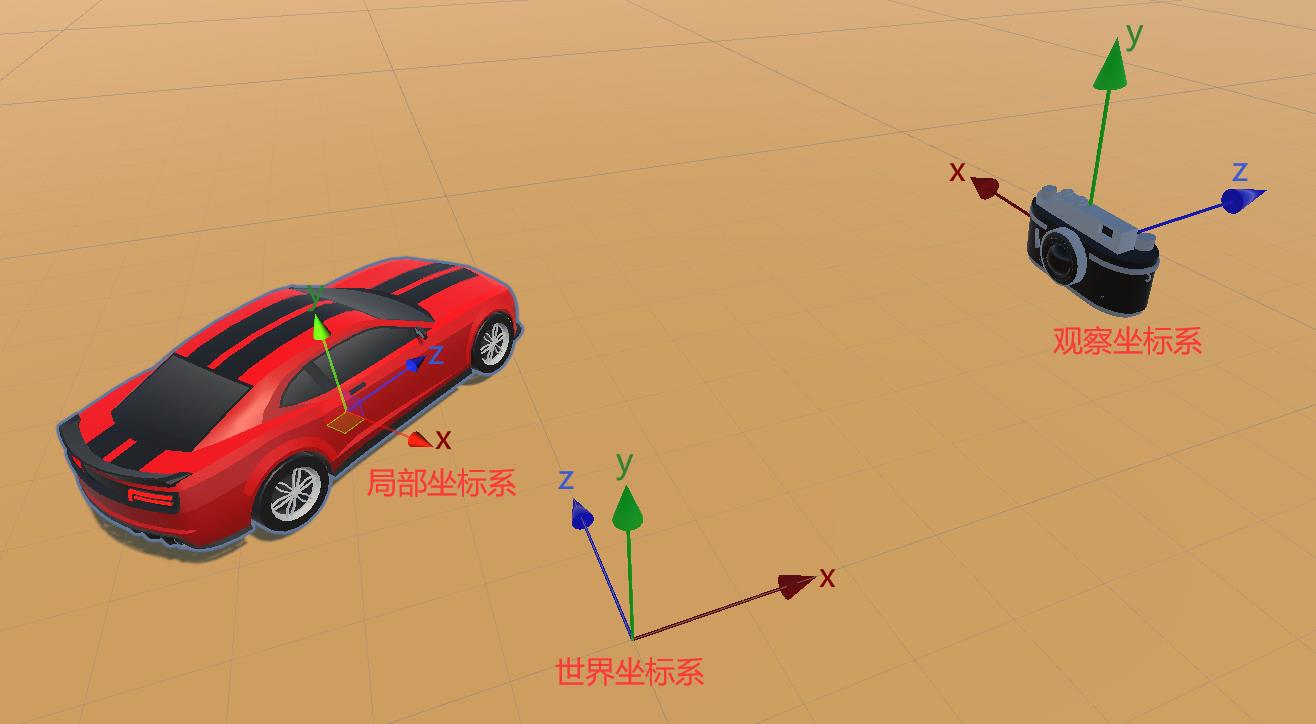
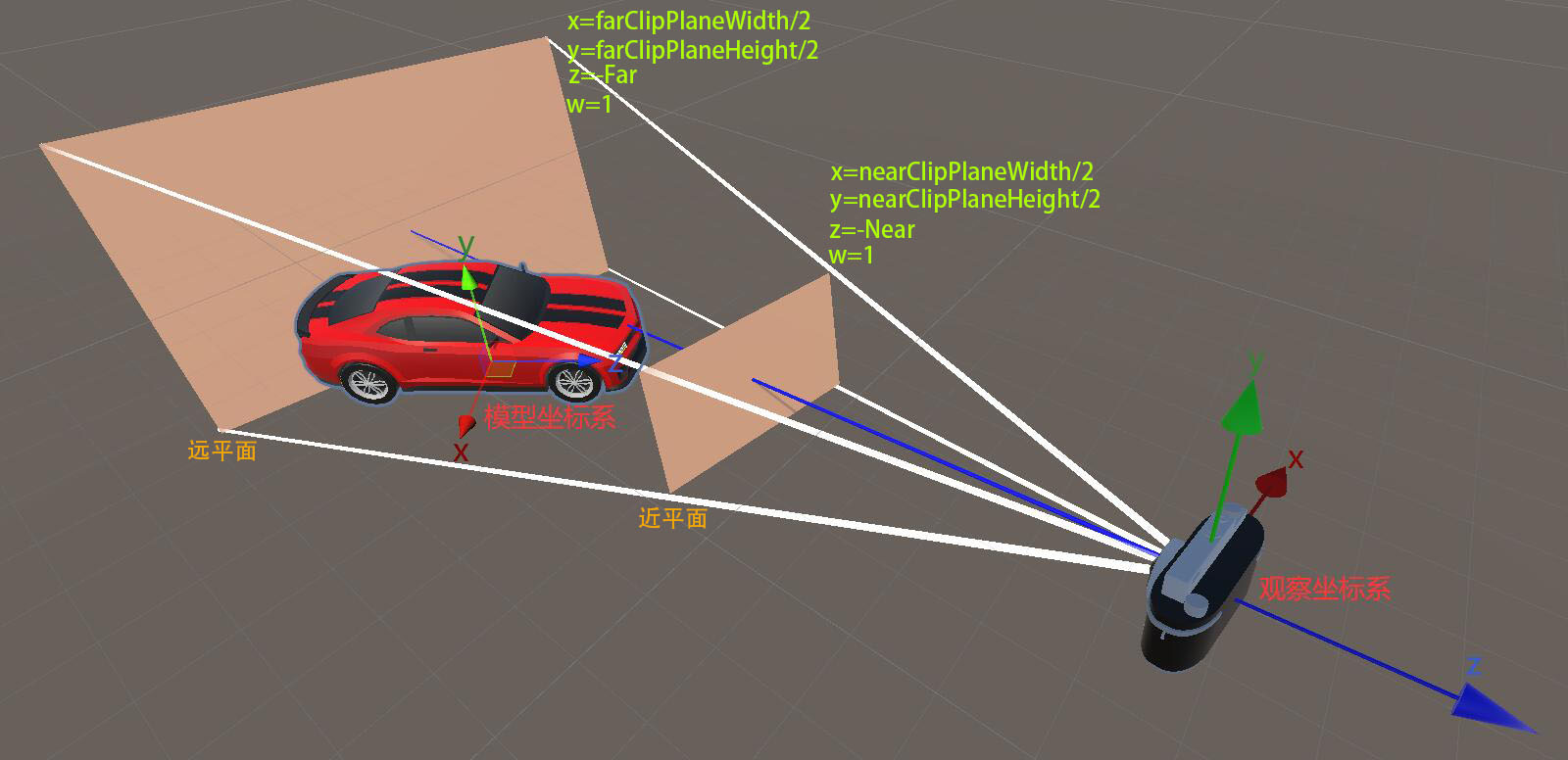
        说明：近平面和远平面间棱台称为视锥体，表示可见区域范围，视锥体以外的顶点数据将被裁剪丢弃。 

裁剪空间

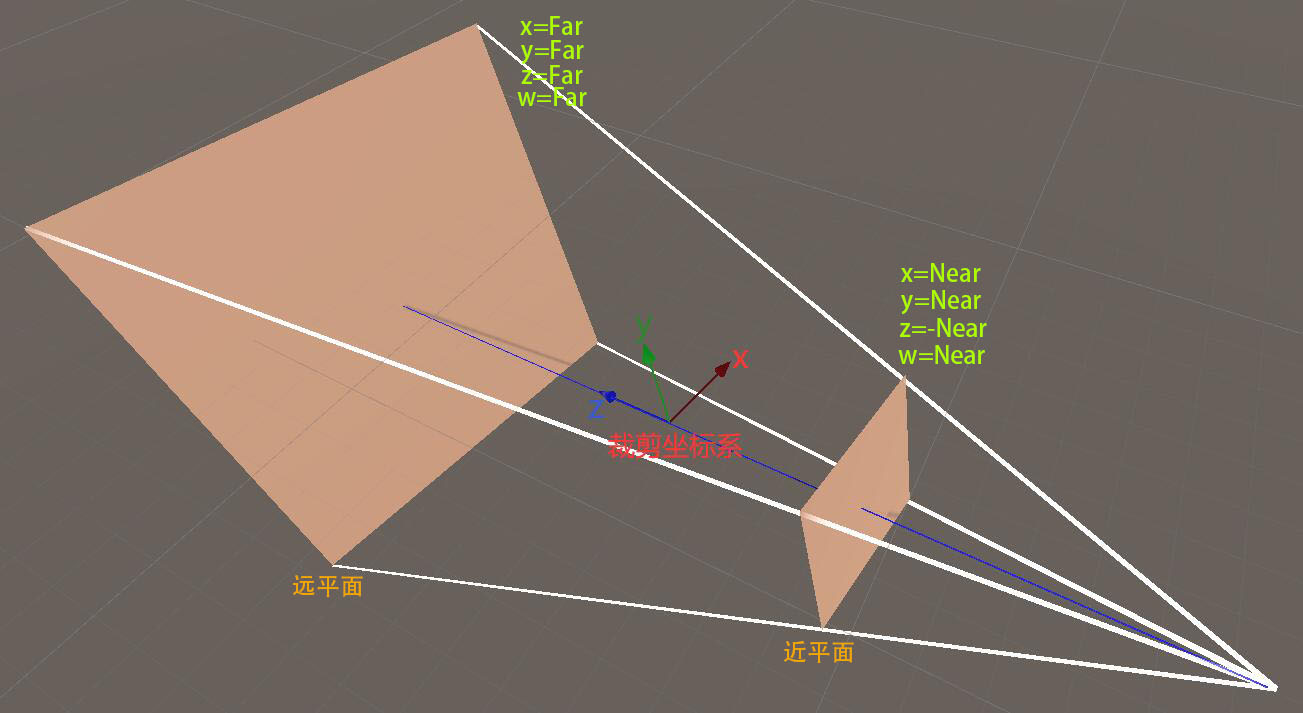
        说明：裁剪空间中的点满足条件：-w < x < w，-w < y < w，-w < z < w，不满足该条件的点将被踢出掉；将满足条件的点 x、y、z 坐标除以 w（齐次除法、透视除法），就会得到归一化设备空间，该空间中的点满足条件：-1 < x < 1，-1 < y < 1，-1 < z < 1。

屏幕空间

2 变换

2.1 模型变换

2.1.1 平移变换

        对于任意点 [x, y, z, 1]'，将其平移 [a, b, c, 0]'，可以使用以下矩阵运算描述平移变换：

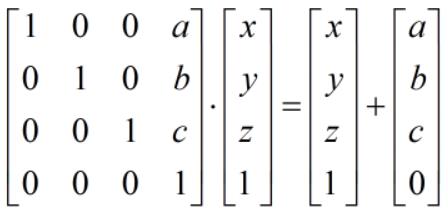
         对于任意向量 [x, y, z, 0]'，将其平移 [a, b, c, 0]'，平移后仍然是 [x, y, z, 0]，如下：

2.1.2 旋转变换

        绕 x 轴旋转 α 度，对应的旋转矩阵如下：

        绕 y 轴旋转 α 度，对应的旋转矩阵如下：

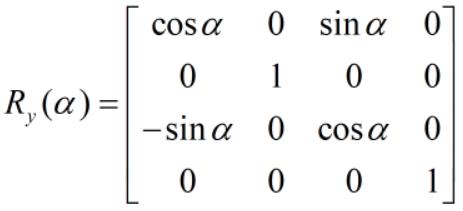
        绕 z 轴旋转 α 度，对应的旋转矩阵如下：

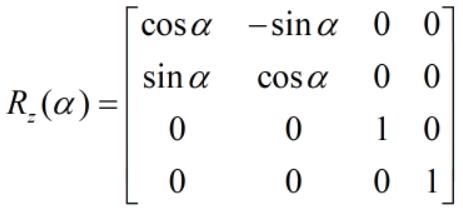
         当旋转角度为 [α, β, γ]' 时，对应的复合旋转矩阵为：

2.1.3 缩放变换

        对于缩放系数 [kx, ky, kz]'，对应的缩放矩阵如下：

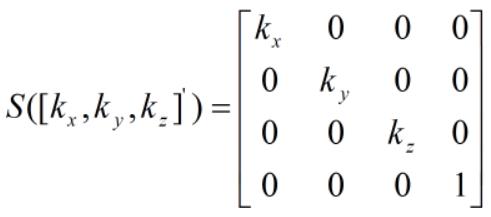
         当 kx = ky = kz 时，该缩放变换称为统一缩放（uniform scale），否则称为非统一缩放（nonuniform scale）。

2.1.4 对称变换

        对于任意点 [x, y, z, 1]'，关于点 [a, b, c, 1]' 对称的点，可以使用以下矩阵运算描述对称变换：

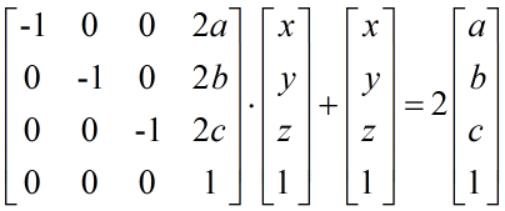
2.2 观察变换

        将世界坐标系按照 1.2 节映射方法扩展到四维空间中，假设 x、y、z、w 轴正方向的的单位向量分别为 e1、e2、e3、e4，相机在世界坐标系下的坐标为 [a, b, c, 1]'，其向右、向上、向前方向的单位向量分别为：r、u、f，则向量 r、u、-f、e4 在一组基向量 e1, e2, e3, e4 下的表示如下：（f 取负是因为观察坐标系是右手坐标系，其 z 轴的正方向与相机的前方方向相反）

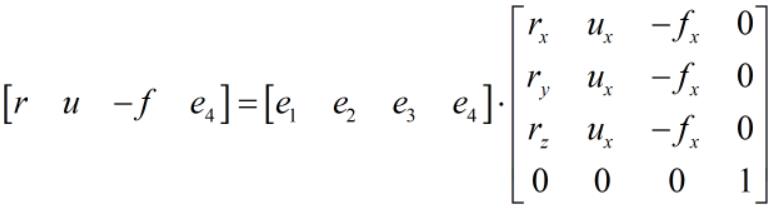
         由于向量 r、u、-f、e4 两两垂直，并且都是单位向量，因此由这 4 个向量组成的矩阵是正交矩阵，即 A-1 = A'。由此可知，向量 e1, e2, e3, e4 在一组基向量 r、u、-f、e4 下的表示如下：

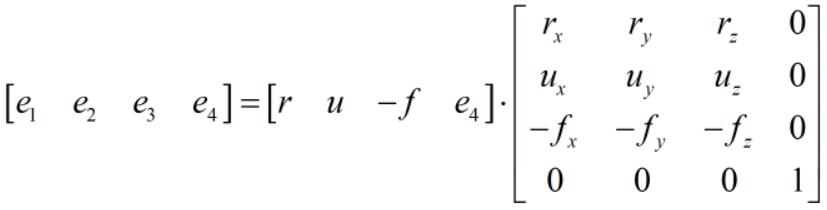
         右侧的矩阵就是坐标轴的旋转变换矩阵，另外还需要进行坐标原点的平移变换，由 1.2.1 节平移变换矩阵可知，观察变换矩阵如下：

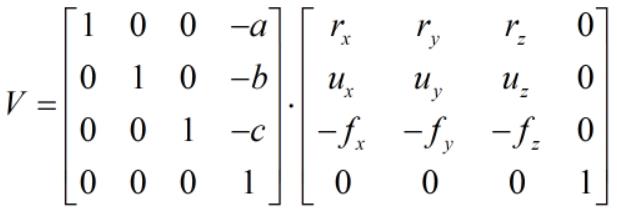
2.3 投影变换

2.3.1 透视投影

        1）透视投影相机参数

        Unity 提供给用户调整透视投影矩阵的参数如下： 

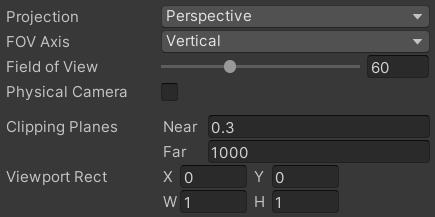
• Near：近平面距离相机的距离；
• Far：远平面距离相机的距离；
• Field of View：视锥体在竖直方向上的张角（以下简称 FOV）；
• Viewport Rect：视口起点和宽高（左下角为原点，向右宽度增加，向上高度增加）

        根据 Near、Far、FOV 的值，可以计算近平面和远平面高度分别为：

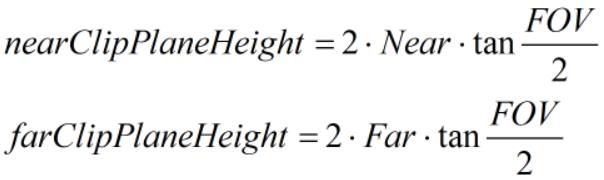
         近平面和远平面的宽度由相机（或屏幕）宽高比决定，假设相机（或屏幕）宽高比为 Aspect，则近平面和远平面的宽度计算如下：

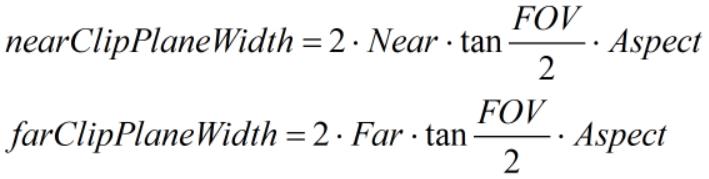
        2）透视投影矩阵推导

        投影的目的是：将模型顶点投影到近平面上，如下，将观察坐标系下的任意顶点 [x0, y0, z0]' 投影到近平面上，投影后的坐标为 [x1, y1, z1]’（z1 = -Near）。

         根据三角形相似原理，存在以下函数关系：

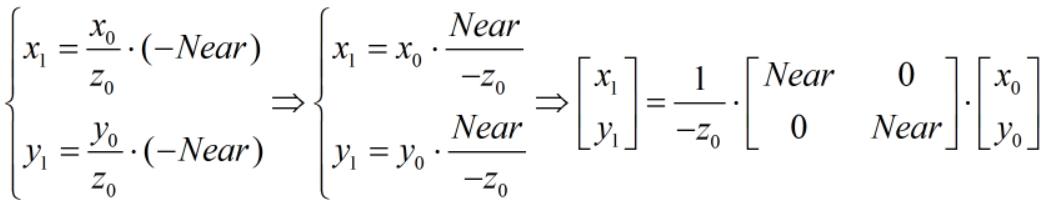
        为了方便后续进行屏幕映射，需要将 [x1, y1]' 进行标准化，即将 x1、y1 映射到区间 [-1, 1]，当前 -nearClipPlaneWidth / 2 ≤ x1 ≤ nearClipPlaneWidth / 2，-nearClipPlaneHeight / 2 ≤ y1 ≤ nearClipPlaneHeight / 2，假设归一化后的坐标为 [x2, y2]，因此存在以下关系：

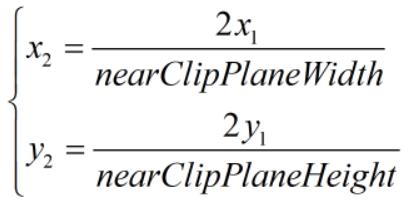
         将 x1、y1、nearClipPlaneWidth、nearClipPlaneHeight 使用 x0、y0、z0、Aspect、FOV 替换得：

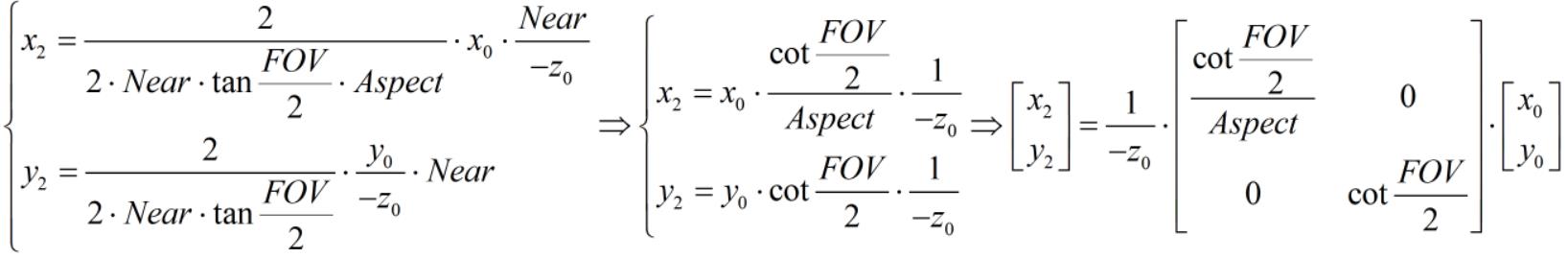
         x2、y2 已标准化，但是当前 -Far ≤ z0 ≤ -Near，我们期望将 z0 也标准化，假设标准化后的变量为 z2，则 -1 ≤ z2 ≤ 1。x2 与 x0、y2 与 y0 的关系式中，都存在 (-1 / z0)，我们期望 z2 与 z0 的关系式中也存在 (-1 / z0)，因此，我们假设 z2 与 z0 的关系如下：

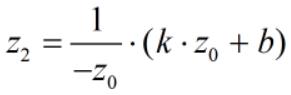
         将 [-Far, 1]'、[-Near, -1]' 代入求解得：（注意：这里不能代入 [-Far, -1]'、[-Near, 1]'，因为裁剪坐标系的 z 轴和 观察坐标系的 z 轴方向相反）

         将 k、b 代入 z2 与 z0 的关系式中得：

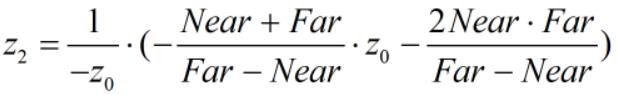
         整理 x2、y2、z2 与 x0、y0、z0 的关系如下：

         由于 z0 是变量，在矩阵前面乘以 (-1 / z0)，使得透视变换不是线性变换，因此我们将原本的透视变换拆分为以下两步：

• 对 [x0, y0, z0, 1]' 左乘透视矩阵；
• 将第一步的结果除以 (-z0)。

         为保证透视变换的线性性质，我们将第二步变换移到屏幕映射中处理，并将其定义为齐次除法（或透视除法），而将第一步变换作为透视变换，其对应的矩阵如下：

        说明：P(4, 3) 定义为 -1 是为了将观察坐标系中顶点的深度信息 (-z) 传递给下一步（齐次除法或透视除法）处理（用 w 存储，即 w = -z），避免深度信息丢失。经透视变换后，顶点坐标的 x、y、z 分量将约束在 [z, -z] 区间，即 [-w, w]，在该区间外的顶点将被丢弃。

        经过透视变换后，观察空间和裁剪空间视锥体的对比如下：

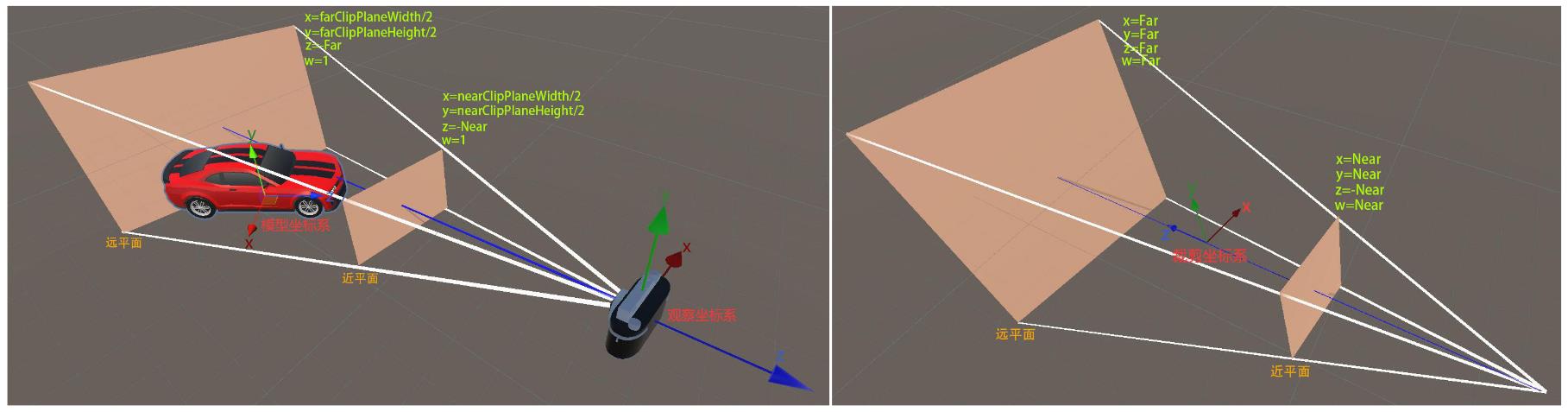
2.3.2 正交投影

        1）正交投影相机参数

        Unity 提供给用户调整正交投影矩阵的参数如下： 

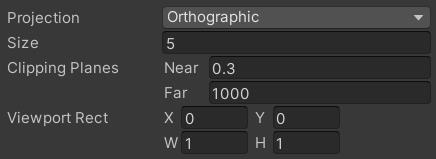
• Size：视锥体在竖直方向上的高度的一半；
• Near：近平面距离相机的距离；
• Far：远平面距离相机的距离；
• Viewport Rect：视口起点和宽高（左下角为原点，向右宽度增加，向上高度增加）

        2）正交投影矩阵推导

        投影的目的是：将模型顶点投影到近平面上，如下，将观察坐标系下的任意顶点 [x0, y0, z0]' 投影到近平面上，投影后的坐标为 [x0, y0, -Near]‘。 

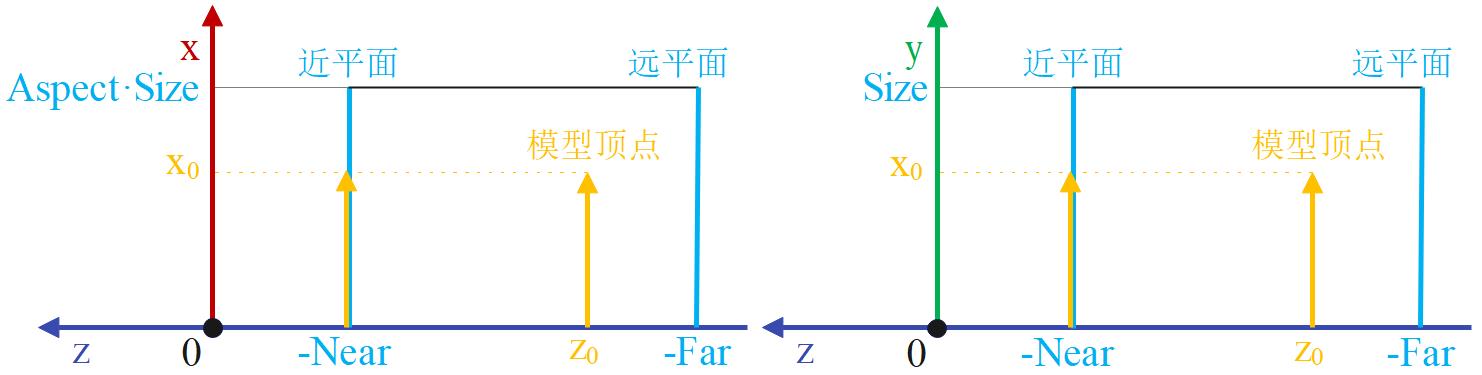
        为了方便后续进行屏幕映射，需要将 [x0, y0, z0]' 进行标准化，即将 x0、y0、z0 映射到区间 [-1, 1]，当前 -Aspect · Size ≤ x1 ≤ Aspect · Size，-Size ≤ y1 ≤ Size，-Far ≤ z0 ≤ -Near，假设归一化后的坐标为 [x1, y1, z1]'，因此存在以下关系：

         说明：正交投影变换后，w 分量的值仍然是 1，从而保证 [x1, y1, z1]' 经齐次除法（除以 w1）后，仍然是标准化坐标（即值域为 [-1, 1]），这样做的好处是：下游不用区分上游传递过来的数据是透视投影还是正交投影处理后的数据。经正交投影变换后，顶点坐标的 x、y、z 分量将约束在 [-1, 1] 区间，在该区间外的顶点将被丢弃。

        经过正交投影变换后，观察空间和裁剪空间视锥体的对比如下：

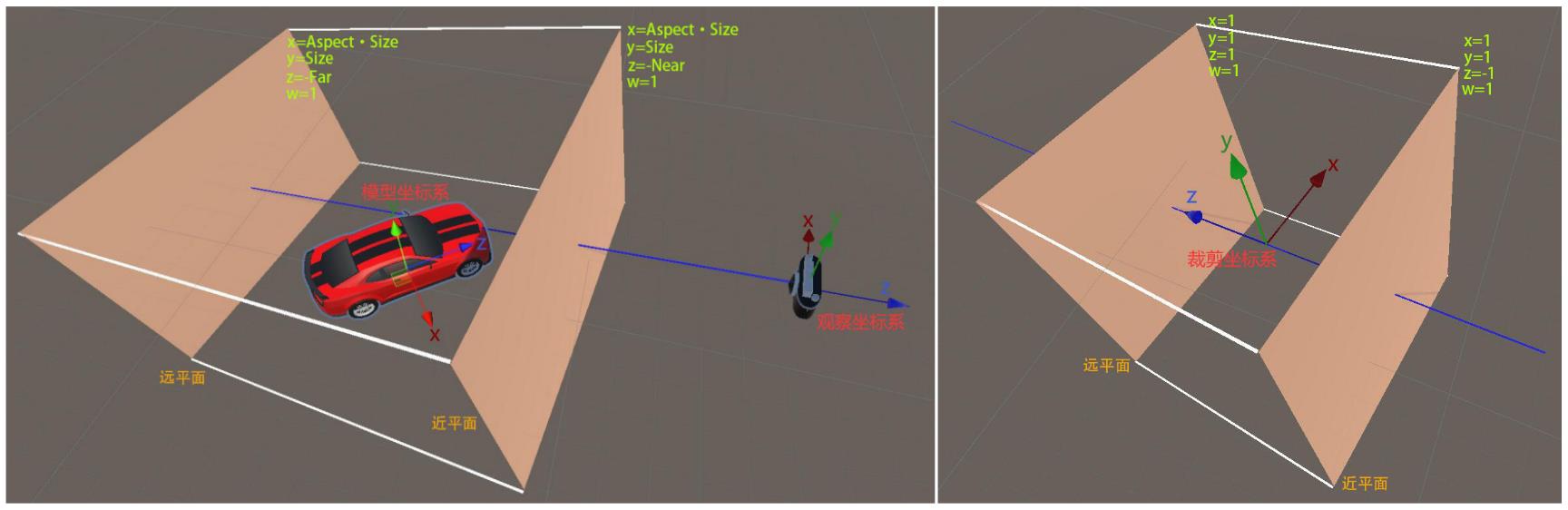
2.4 齐次除法和屏幕映射

2.4.1 齐次除法

        经透视投影或正交投影后，将坐标 [x, y, z, w] 中的 x、y、z 分量都除以其 w 分量的值，使得 x、y、z 都约束在 [-1, 1] 区间，该过程称为齐次除法（或透视除法），得到的坐标称为归一化的设备坐标（NDC）。

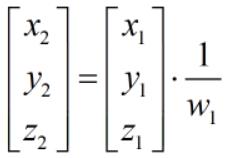
2.4.2 屏幕映射

        经齐次除法后，将坐标的 x、y 值映射到屏幕像素位置，该过程称为屏幕映射。映射前 x、y 的值域为 [-1, 1]，映射后 x 的值域为 [0, pixelWidth]，y 的值域为 [0, pixelHeight]，屏幕左下角坐标为 [0, 0]，右上角坐标为 [pixelWidth, pixelHeight]。屏幕映射公式如下：

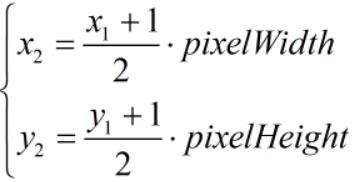
2.5 法线变换

        假设模型变换为 M，模型空间中某点法线向量为 n，如果模型变换中包含非统一缩放（即 x、y、z 的缩放系数不全相等）， 此时若按照 M · n 计算法线的世界坐标，就会出现变换后的法线与切面不垂直，如下图。

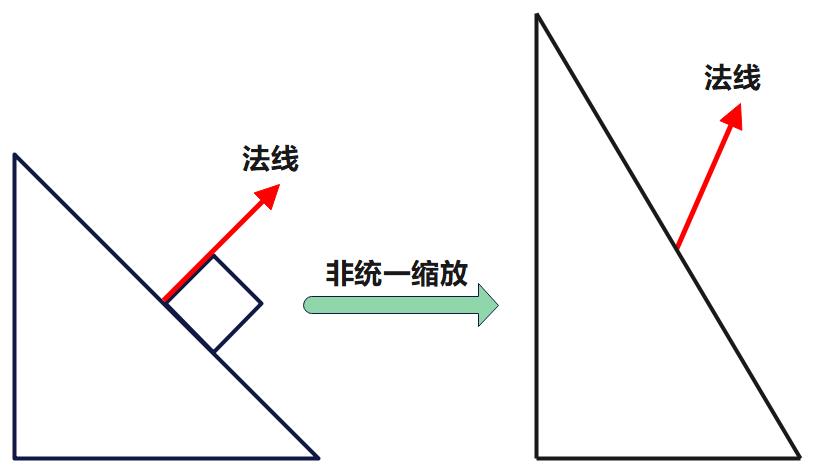
        法线由切线计算而来，在模型空间中 A 点的切线向量为 v1，法线向量为 n1，经过模型变换（矩阵 M）后，切线向量为 v2，法线向量为 n2，假设法线向量的变换矩阵为 G，因此存在以下关系： 

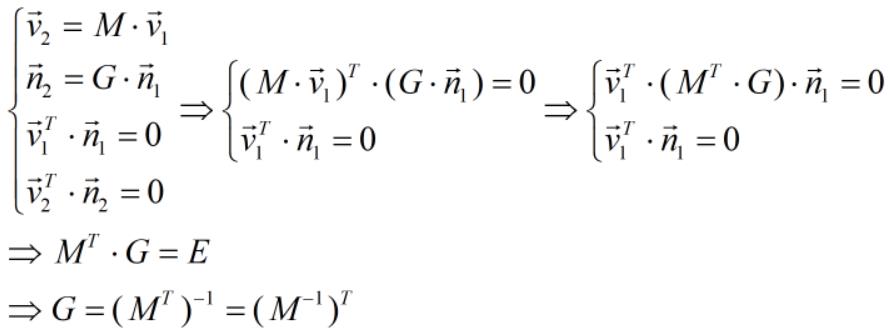
        Unity 中线性变换主要有平移、旋转、缩放，由于向量不受平移变换影响，因此，对于法线向量而言，只受旋转和缩放影响。

• 当 M 只包含旋转变换时，M 是正交矩阵，，因此 G = M；
• 当 M 只包含统一缩放变换时，M = k·E，因此 G = 1/k·E = 1/(k^2)·M，由于法线向量只需要方向，后面会进行归一化，因此可以简写 G = M；
• 当 M 只包含旋转变换和统一缩放变换时，G = 1/(k^2)·M，由于法线向量只需要方向，后面会进行归一化，因此可以简写 G = M；

        Unity 中法线变换源码如下：

        UnityCG.cginc

// 局部空间->世界空间
float3 UnityObjectToWorldNormal(float3 norm) 
#ifdef UNITY_ASSUME_UNIFORM_SCALING // 统一缩放(x、y、z分量缩放系数一致)
    return UnityObjectToWorldDir(norm); // normalize(mul((float3x3)unity_ObjectToWorld, norm))
#else
    return normalize(mul(norm, (float3x3)unity_WorldToObject)); // mul(IT_M, norm) => mul(norm, I_M)
#endif