02- 天池工业蒸汽量项目实战 (项目二)

Posted 2023-03-03 处女座_三月

• 忽略警告: warnings.filterwarnings("ignore")

import warnings
warnings.filterwarnings("ignore")

• 读取文件格式: pd.read_csv(train_data_file, sep='\\t')  # 注意sep 是 ',' , 还是'\\t'
• train_data.info()     # 查看是否存在空数据及数据类型
• train_data.describe()   # 查看数据分布
• 删除无关特征: train_data_drop = train_data.drop(['V5','V9','V11','V17','V22','V28'], axis=1)
• 获取特征相关性: train_corr = train_data_drop.corr()
• 同时删除训练数据和测试数据分布不均匀的特征:
  • train_data.drop(drop_col_kde,axis = 1,inplace=True)

• all_data.to_csv('./processed_zhengqi_data.csv',index=False)   # 保存数据
• 最大值最小值:  min_max_scaler.fit_transform(all_data[columns])

from sklearn import preprocessing 
min_max_scaler = preprocessing.MinMaxScaler()
all_data_normed = min_max_scaler.fit_transform(all_data[columns])  # 归一化
all_data_normed = pd.DataFrame(all_data_normed,columns=columns)  # 转换为dataframe

• 时间判定:   %%time

---

工业蒸汽量预测

项目描述

        经脱敏后的锅炉传感器采集的数据（采集频率是分钟级别），根据锅炉的工况，预测产生的蒸汽量。

        火力发电的基本原理是：燃料在燃烧时加热水生成蒸汽，蒸汽压力推动汽轮机旋转，然后汽轮机带动发电机旋转，产生电能。在这一系列的能量转化中，影响发电效率的核心是锅炉的燃烧效率，即燃料燃烧加热水产生高温高压蒸汽。锅炉的燃烧效率的影响因素很多，包括锅炉的可调参数，如燃烧给量，一二次风，引风，返料风，给水水量；以及锅炉的工况，比如锅炉床温、床压，炉膛温度、压力，过热器的温度等。

天池官网链接: 工业蒸汽量预测_学习赛_天池大赛-阿里云天池

第一部分 数据探索

1.1 导入数据探索工具包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats

1.2 加载数据

• csv是 txt 格式 .

train_data_file = "./zhengqi_train.txt"
test_data_file =  "./zhengqi_test.txt"

train_data = pd.read_csv(train_data_file, sep='\\t')
test_data = pd.read_csv(test_data_file, sep='\\t')
train_data.head()

1.3 查看数据集变量信息

1.3.1 查看数据集字段信息

test_data.head()   # 查看开始部分的数据信息

1.3.2 查看详细数据信息

测试集数据共有1925个样本，数据中有V0-V37共计38个特征变量，变量类型都为数值类型。

train_data.info()     # 查看数据详情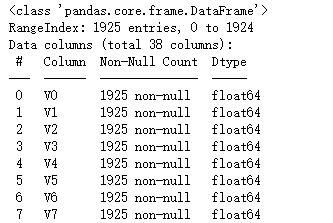

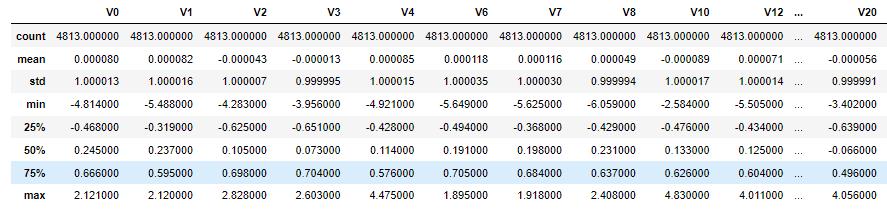
1.3.3 查看数据统计信息

train_data.describe()   # 查看数据分布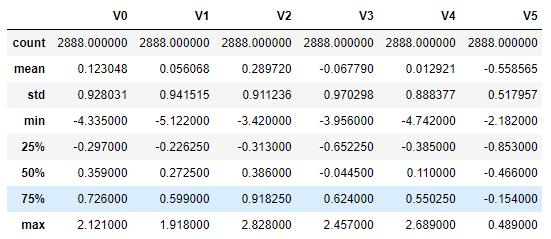

 

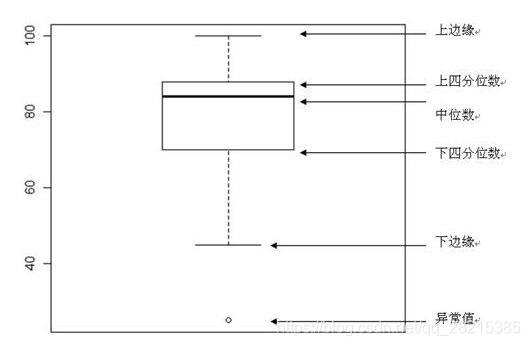
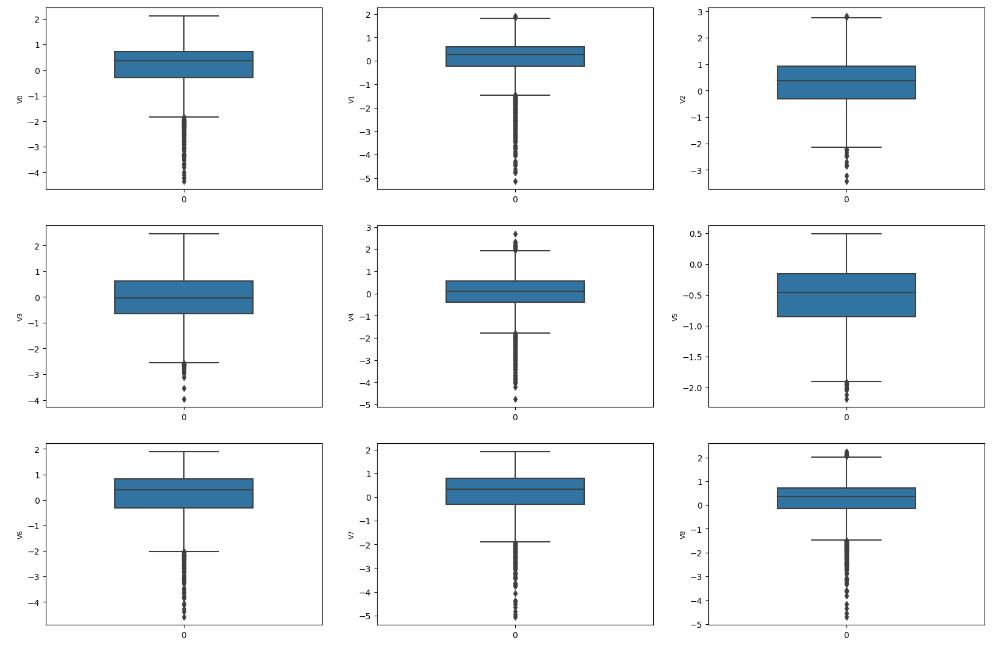
1.3.4 箱式图数据探索

fig = plt.figure(figsize=(6, 4))    # 指定绘图对象宽度和高度
sns.boxplot(train_data['V0'],width=0.5)
plt.savefig('./2-特征箱式图.jpg',dpi = 200)

# 画箱式图
column = train_data.columns.tolist()[:39]  # 列表头

fig = plt.figure(figsize=(20, 60))  # 指定绘图对象宽度和高度
for i in range(38):
    plt.subplot(13, 3, i + 1)       # 13行3列子图
    sns.boxplot(train_data[column[i]], width=0.5)  # 箱式图
    plt.ylabel(column[i], fontsize=8)

箱型图的作用:

• 直观明了地识别数据批中的异常值
• 利用箱线图判断数据批的偏态和尾重

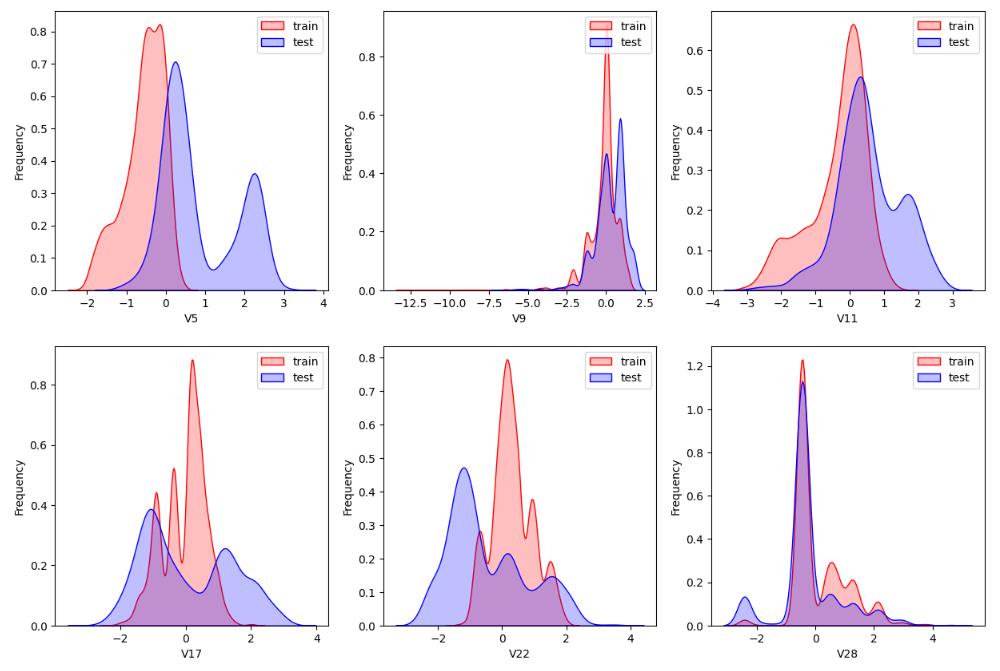
1.4 数据分布查看

• sns.kdeplot()  查看训练数据和测试数据的对比, 是否分布一致 .

dist_cols = 6
dist_rows = len(test_data.columns)//6 + 1

plt.figure(figsize=(4*dist_cols,4*dist_rows))

i=1
for col in test_data.columns:
    ax=plt.subplot(dist_rows,dist_cols,i)
    
    ax = sns.kdeplot(train_data[col], color="Red", shade=True)
    ax = sns.kdeplot(test_data[col], color="Blue", shade=True)
    
    ax.set_xlabel(col)
    ax.set_ylabel("Frequency")
    ax = ax.legend(["train","test"])
    i+=1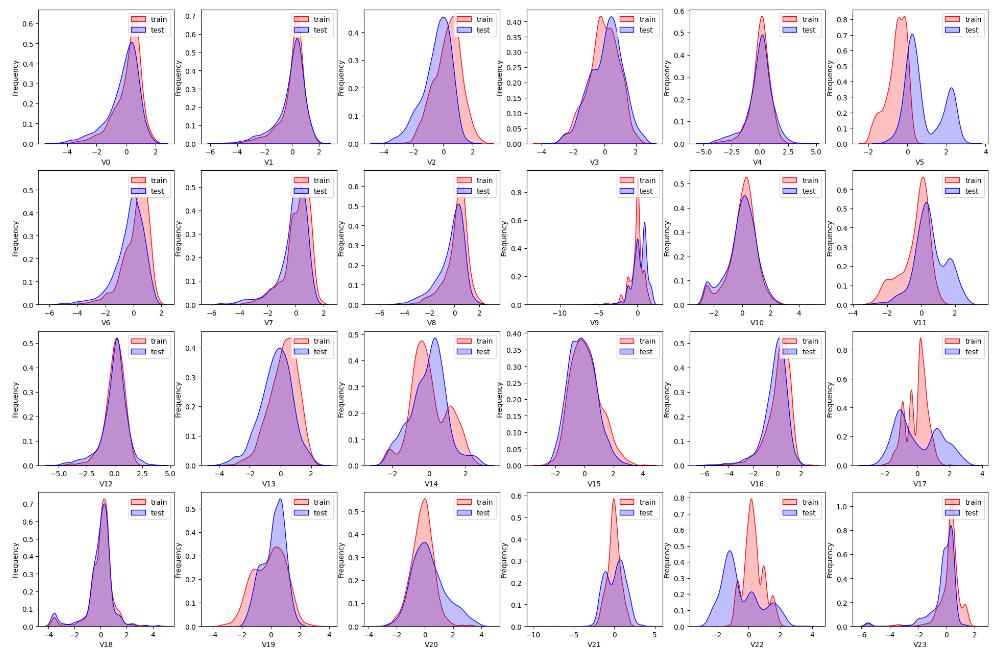

 查看指定特征(查看特征'V5', 'V17', 'V28', 'V22', 'V11', 'V9'数据的数据分布):

col = 3
row = 2
plt.figure(figsize=(5 * col,5 * row))
i=1
for c in ["V5","V9","V11","V17","V22","V28"]:
    ax = plt.subplot(row,col,i)
    ax = sns.kdeplot(train_data[c], color="Red", shade=True)
    ax = sns.kdeplot(test_data[c], color="Blue", shade=True)
    ax.set_xlabel(c)
    ax.set_ylabel("Frequency")
    ax = ax.legend(["train","test"])
    i+=1
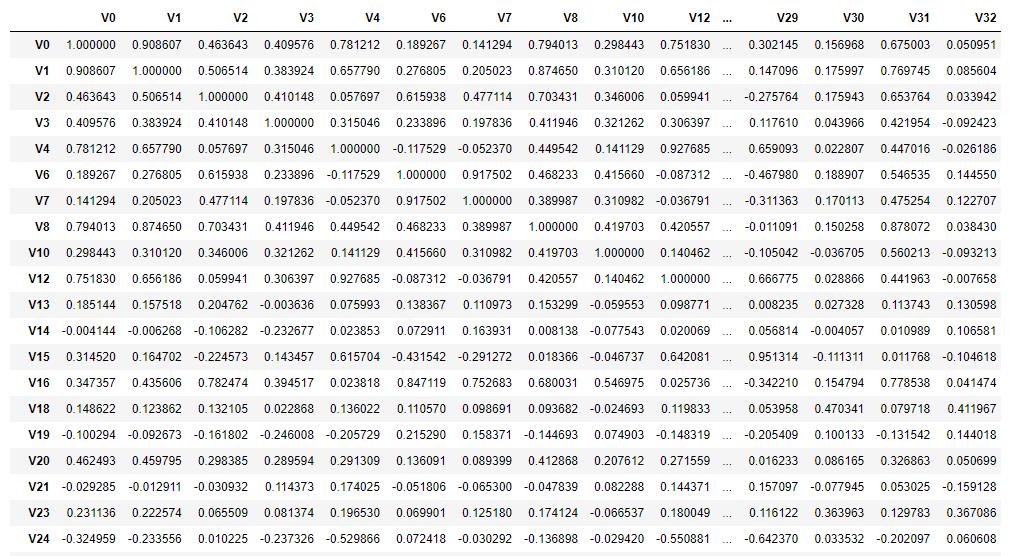
plt.savefig('./4-数据分布.jpg',dpi = 200)

 1.5 特征相关性

• train_corr = train_data_drop.corr()       # 求取数据的相关性系数

drop_col_kde = ['V5','V9','V11','V17','V22','V28']
train_data_drop = train_data.drop(drop_col_kde, axis=1)
train_corr = train_data_drop.corr()
train_corr

 1.5.1 热力图 (相关性显示)

• mask = np.zeros_like(mcorr, dtype=np.bool)     # 构造与mcorr同维数矩阵 为bool型
• mask[np.triu_indices_from(mask)] = True     # 角分线右侧为True,右上角设置为True
• g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, fmt='0.2f')   # 画热力图

plt.figure(figsize=(24, 20))  # 指定绘图对象宽度和高度
colnm = train_data_drop.columns.tolist()  # 列表头
# 相关系数矩阵，即给出了任意两个变量之间的相关系数
mcorr = train_data_drop.corr()

# 构造与mcorr同维数矩阵 为bool型
mask = np.zeros_like(mcorr, dtype=np.bool) # False

# 角分线右侧为True,右上角设置为True（戴面具，看不见）
mask[np.triu_indices_from(mask)] = True

# 设置colormap对象，表示颜色
cmap = sns.diverging_palette(220, 10, as_cmap=True)

# 热力图（看两两相似度）
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')  
plt.savefig('./5-特征相关性.jpg',dpi = 400)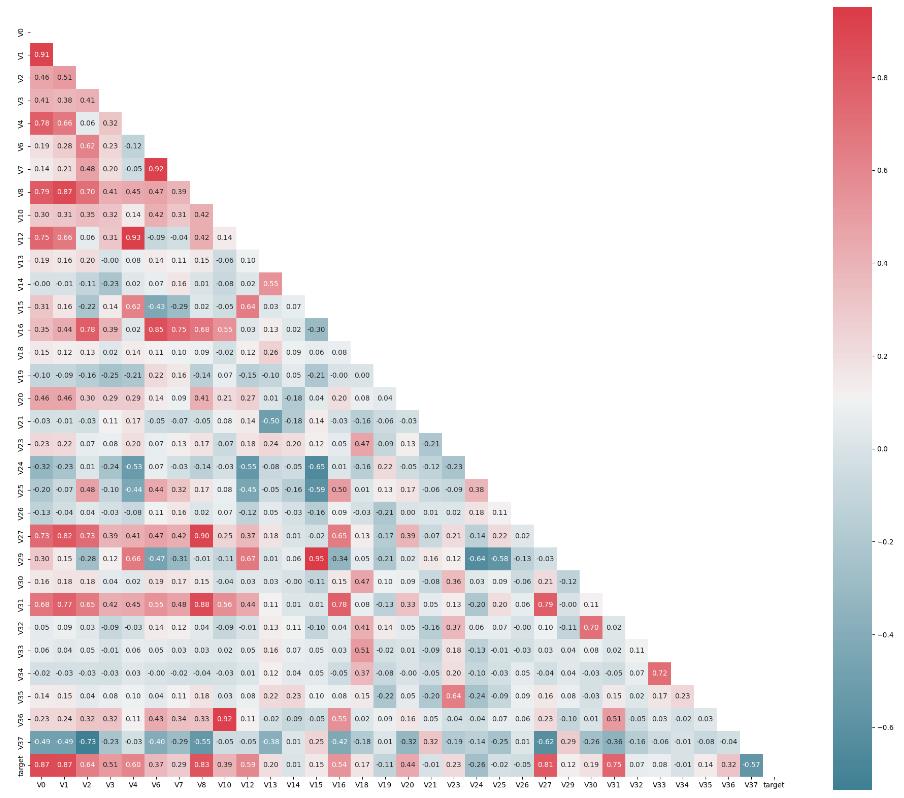

1.6 特征筛选

1.6.1 根据数据分布进行特征删除

• 根据数据分布判定是否删除 , 根据前方的显示图对比

# 删除训练数据和预测数据 分布不均匀，不够正太分布的特征
train_data.drop(drop_col_kde,axis = 1,inplace=True)
test_data.drop(drop_col_kde,axis = 1,inplace= True)
train_data.head()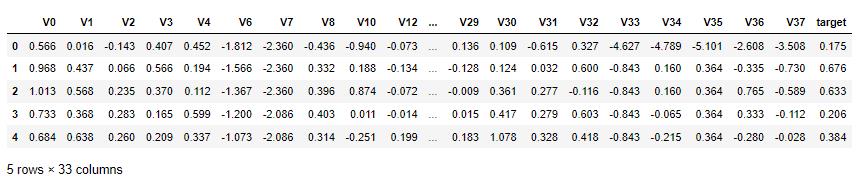

 1.6.2 根据相关性系数进行特征筛选

• cond = mcorr[ 'target' ].abs() < 0.1     # 根据相关性判定
• drop_col_corr = mcorr.index[ cond ]

cond = mcorr['target'].abs() < 0.1
drop_col_corr = mcorr.index[cond]
display(drop_col_corr)  # ['V14', 'V21', 'V25', 'V26', 'V32', 'V33', 'V34']
# 删除
train_data.drop(drop_col_corr,axis = 1,inplace=True)
test_data.drop(drop_col_corr,axis = 1,inplace=True)
train_data.head()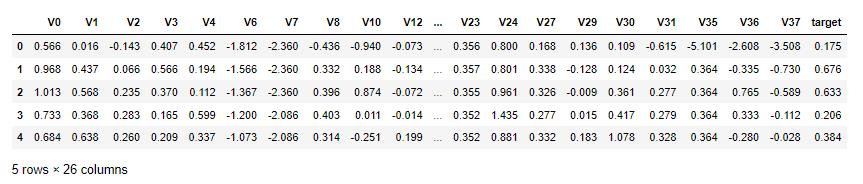

 1.7 数据保存

• train_data[ 'label' ] = 'train'     # 添加标签
• data.to_csv(./data.csv, index=False)

train_data['label'] = 'train'
test_data['label'] = 'test'
all_data = pd.concat([train_data,test_data])
all_data.to_csv('./processed_zhengqi_data.csv',index=False)
all_data.head()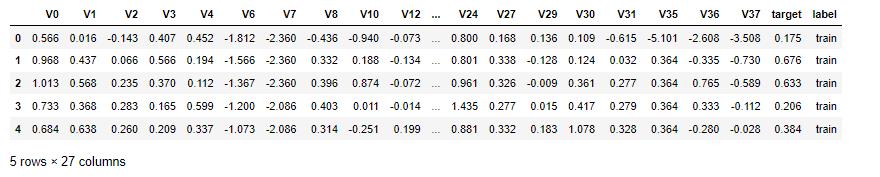

---

第二部分 特征工程

2.1 导入数据分析工具包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
from sklearn import preprocessing 
import warnings
warnings.filterwarnings("ignore")

2.2 数据加载

all_data = pd.read_csv('./processed_zhengqi_data.csv')
all_data.head()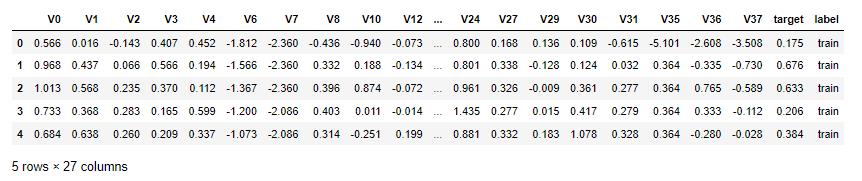

2.3 最大值最小值归一化

2.3.1 归一化之前数据查看

# 特征归一化
columns=list(all_data.columns)
# 删除标签列索引
columns.remove('label')
# 删除目标值
columns.remove('target')
all_data[columns].describe()

2.3.2 sklearn自带方法最大值最小值归一化

# 导包
from sklearn import preprocessing 
min_max_scaler = preprocessing.MinMaxScaler()
# 处理完后，数据变换为Numpy数组
all_data_normed = min_max_scaler.fit_transform(all_data[columns])
all_data_normed = pd.DataFrame(all_data_normed,columns=columns)
all_data_normed.describe()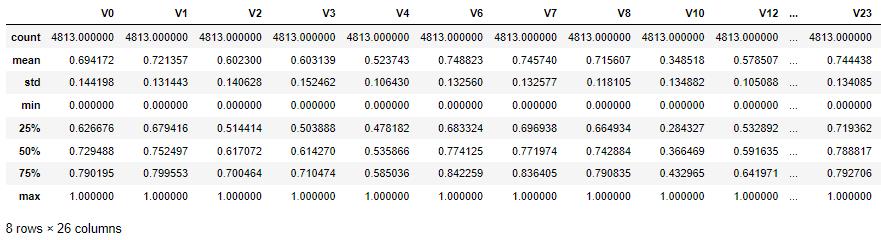

 2.3.3 数据正态化操作（Box-Cox变换）

查看特征变量‘V0’的数据分布直方图、并绘制Q-Q图（概率图）查看数据是否近似于正态分布、特征目标值相关性 .

skew函数计算数据集的偏度：

• skew = 0，正态分布
• skew > 0，偏移了右边
• skew < 0，偏移了左边

查看所有特征原始的直方图、Q-Q图、特征目标值散点图

# 获取训练数据
cond = all_data['label'] == 'train'
train_data = all_data[cond]
train_data.drop(labels='label',axis = 1,inplace=True)

fcols = 3
columns = list(train_data.columns)
columns.remove('target')
frows = len(columns)
plt.figure(figsize=(4*fcols,4*frows))
i=0
for col in columns:
    feature = train_data[[col, 'target']]
        
    i+=1
    plt.subplot(frows,fcols,i)
    sns.distplot(feature[col] , fit=stats.norm);
    plt.title(col)
    plt.xlabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(feature[col], plot=plt)
    plt.title('skew='+':.4f'.format(stats.skew(feature[col])))
    plt.xlabel('')
    plt.ylabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(feature[col], feature['target'],'.',alpha=0.5)
    plt.title('corr='+':.2f'.format(np.corrcoef(feature[col],
                                                  feature['target'])[0][1]))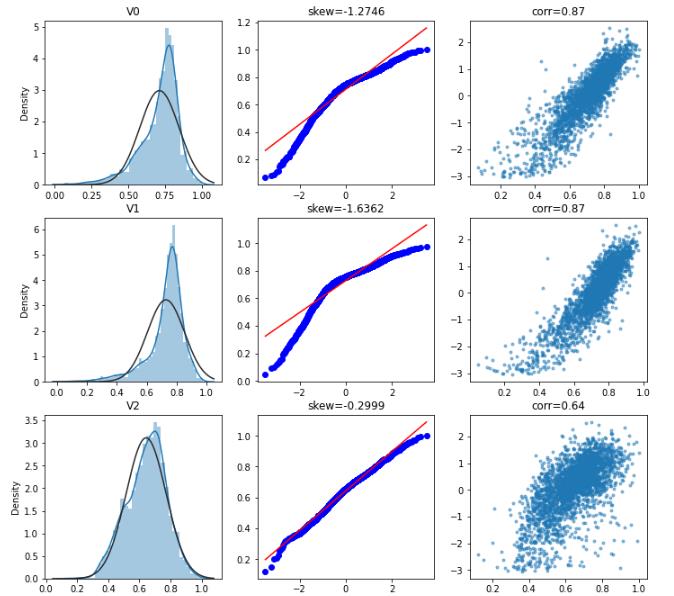

对特征，进行Box-Cox变换，Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性，对许多实际数据都是行之有效的 .

# 绘图显示Box-Cox变换对数据分布影响
fcols = 6
columns = list(train_data.columns)
columns.remove('target')
frows = len(columns)
plt.figure(figsize=(4*fcols,4*frows))
i=0
def norm_min_max(feature):
    return (feature-feature.min())/(feature.max()-feature.min())

for col in columns:
    feature = train_data[[col, 'target']].dropna()

    i+=1
    plt.subplot(frows,fcols,i)
    sns.distplot(feature[col] , fit=stats.norm);
    plt.title(col+' raw')
    plt.xlabel('')

    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(feature[col], plot=plt)
    plt.title('skew='+':.4f'.format(stats.skew(feature[col])))
    plt.xlabel('')
    plt.ylabel('')

    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(feature[col], feature['target'],'.',alpha=0.5)
    plt.title('corr='+':.2f'.format(np.corrcoef(feature[col],
                                                  feature['target'])[0][1]))
    
    # Box-Cox转变，视图可视化
    i+=1
    plt.subplot(frows,fcols,i)
    trans_feature, lambda_feature = stats.boxcox(feature[col].dropna()+1)
    trans_feature = norm_min_max(trans_feature)      
    sns.distplot(trans_feature , fit=stats.norm);
    plt.title(col+' Tramsformed')
    plt.xlabel('')

    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(trans_feature, plot=plt)
    plt.title('skew='+':.4f'.format(stats.skew(trans_feature)))
    plt.xlabel('')
    plt.ylabel('')

    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(trans_feature, feature['target'],'.',alpha=0.5)
    plt.title('corr='+':.2f'.format(np.corrcoef(trans_feature,
                                                  feature['target'])[0][1]))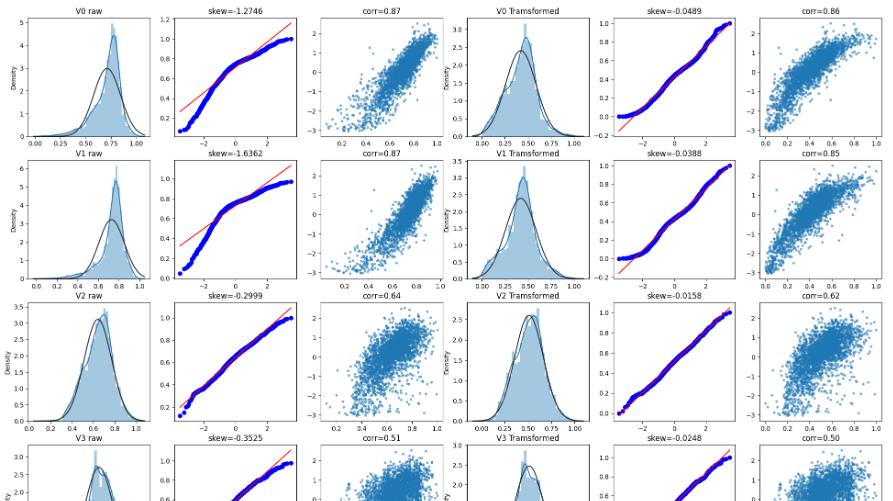

 从回归结果可见，经过Box-Cox变换数据分布，更加正态化，所以进行Box-Cox变换很有必要
Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法，是统计建模中常用的一种数据变换，用于连续的响应变量不满足正态分布的情况
Box-Cox变换的一般形式为:

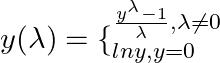
# 进行Box-Cox变换
columns=list(all_data.columns)
# 删除标签列索引
columns.remove('label')
# 删除目标值
columns.remove('target')
for col in columns:   
    # transform column
    all_data.loc[:,col], _ = stats.boxcox(all_data.loc[:,col]+1)

2.4 定义数据获取方法

from sklearn.model_selection import train_test_split
def get_train_data():
    train_data = all_data[all_data["label"]=="train"]
    # 数据拆分：训练数据和验证数据
    y = train_data.target
    X = train_data.drop(["label","target"],axis=1)
    return X,y
# 提取训练和验证数据
def split_train_data():
    train_data = all_data[all_data["label"]=="train"]
    # 数据拆分：训练数据和验证数据
    y = train_data.target
    X = train_data.drop(["label","target"],axis=1)
    X_train,X_valid,y_train,y_valid=train_test_split(X,y,test_size=0.2)
    return X_train,X_valid,y_train,y_valid

# 提取预测数据
def get_test_data():
    # 参数drop = True，表示将原来的行索引，直接删除
    test_data = all_data[all_data["label"]=="test"].reset_index(drop=True)
    return test_data.drop(["label","target"],axis=1)

2.5 异常值过滤

# 基于模型预测的异常值检测
from sklearn.metrics import mean_squared_error

def find_outliers(model, X, y, sigma = 3):
    # 模型训练
    model.fit(X,y)
    y_pred = pd.Series(model.predict(X), index=y.index)
    
    # 计算预测值和真实值之差
    resid = y - y_pred
    mean_resid = resid.mean()
    std_resid = resid.std()
    
    # 异常值计算
    z = (resid - mean_resid)/std_resid # Z-score归一化 
    outliers = z[abs(z)>sigma].index # 正太分布异常值过滤：3σ法则
    
    # 输出模型评价
    print('R2=',model.score(X,y))
    print("mse=",mean_squared_error(y,y_pred))
    print('---------------------------------------')

    # 残差数据
    print('mean of residuals:',mean_resid)
    print('std of residuals:',std_resid)
    print('---------------------------------------')
    
    # 异常值点
    print(len(outliers),'outliers:')
    print(outliers.tolist())

    # 数据可视化
    # 真实值预测值散点图
    plt.figure(figsize=(15,5))
    ax_131 = plt.subplot(1,3,1)
    plt.plot(y,y_pred,'.')
    plt.plot(y.loc[outliers],y_pred.loc[outliers],'ro')
    plt.legend(['Accepted','Outlier'])
    plt.xlabel('y')
    plt.ylabel('y_pred');
    
    # 真实值和残差散点图
    ax_132=plt.subplot(1,3,2)
    plt.plot(y,y-y_pred,'.')
    plt.plot(y.loc[outliers],y.loc[outliers]-y_pred.loc[outliers],'ro')
    plt.legend(['Accepted','Outlier'])
    plt.xlabel('y')
    plt.ylabel('y - y_pred');

    # 直方图
    ax_133=plt.subplot(1,3,3)
    z.plot.hist(bins=50,ax=ax_133)
    z.loc[outliers].plot.hist(color='r',bins=50,ax=ax_133)
    plt.legend(['Accepted','Outlier'])
    plt.xlabel('z')
    
    plt.savefig('outliers.png',dpi = 200)
    
    return outliers

2.5.1 岭回归算法查找异常值

# 获取训练数据
from sklearn.linear_model import Ridge
X_train, y_train = get_train_data()

# 使用岭回归查找异常值
outliers1 = find_outliers(Ridge(), X_train, y_train)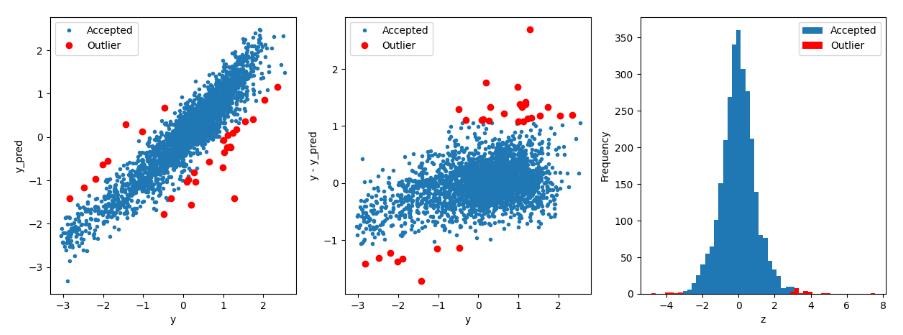

 2.5.2 套索回归算法查找异常值

# 获取训练数据
from sklearn.linear_model import Lasso
X_train, y_train = get_train_data()
# 使用岭回归查找异常值
outliers2 = find_outliers(Lasso(), X_train, y_train)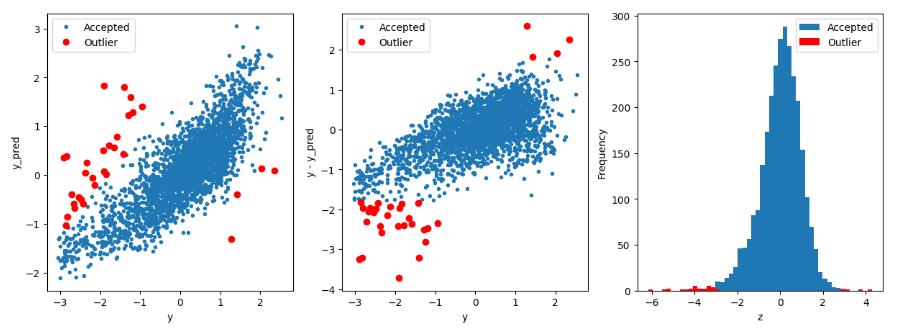

 2.5.3 支持向量机SVR算法查找异常值

# 获取训练数据
from sklearn.svm import SVR
X_train, y_train = get_train_data()

# 使用岭回归查找异常值
outliers3 = find_outliers(SVR(), X_train, y_train)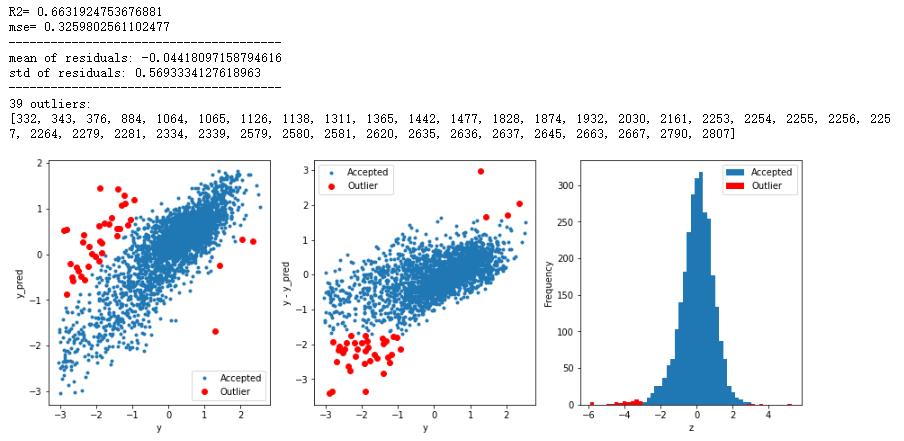

 2.5.4 Xgboost算法查找异常值

# 获取训练数据
from xgboost import XGBRegressor
X_train, y_train = get_train_data()
# 使用岭回归查找异常值
outliers4 = find_outliers(XGBRegressor(), X_train, y_train)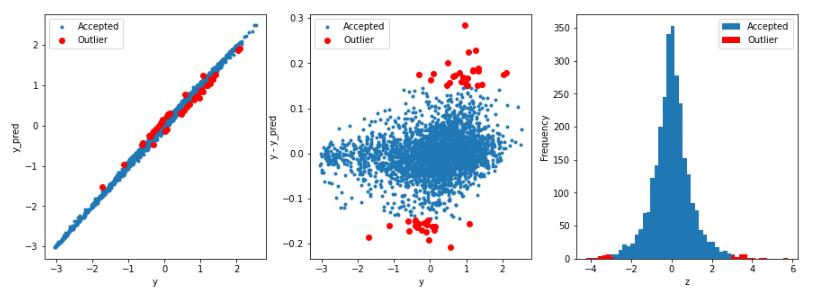

2.5.5 过滤异常值

outliers12 = np.union1d(outliers1,outliers2)
outliers34 = np.union1d(outliers3,outliers4)
outliers = np.union1d(outliers12,outliers34)
display(outliers)
# 过滤异常值
all_data = all_data.drop(labels=outliers)
all_data.to_csv('./processed_zhengqi_data2.csv',index=False)
all_data.shape

 

2.6 多重共线性

2.6.1 查看原数据方差膨胀因子

# 安装相应库 pip install statsmodels
# 多重共线性方差膨胀因子
from statsmodels.stats.outliers_influence import variance_inflation_factor
#多重共线性
X_train,y_train = get_train_data()
X_train = np.matrix(X_train)
VIF_list=[round(variance_inflation_factor(X_train, i),
                2) for i in range(X_train.shape[1])]
print(VIF_list)

2.6.2 PCA降维

from sklearn.decomposition import PCA
pca = PCA(n_components = 22,whiten=True)

X_train,y_train = get_train_data()
X_train_pca = np.matrix(pca.fit_transform(X_train))
VIF_pca_list=[round(variance_inflation_factor(X_train_pca,
                    i),2) for i in range(X_train_pca.shape[1])]
print(VIF_pca_list)
# 数据保存
np.savez('./train_data_pca',X_train = X_train_pca,y_train = y_train)

X_test = get_test_data()
X_test_pca = pca.transform(X_test)

# 查看数据
display(X_test_pca)
# 数据保存
np.savez('./test_data_pca',X_test = X_test_pca)

2.7 模型初验

2.7.1 导入相关库

from sklearn.linear_model import LinearRegression     # 线性回归
from sklearn.neighbors import KNeighborsRegressor     # K近邻回归
from sklearn.tree import DecisionTreeRegressor        # 决策树回归
from sklearn.ensemble import RandomForestRegressor    # 随机森林回归
from sklearn.svm import SVR   # 支持向量回归
import lightgbm as lgb        # lightGbm模型
from sklearn.ensemble import GradientBoostingRegressor

from sklearn.model_selection import train_test_split  # 切分数据
from sklearn.metrics import mean_squared_error        # 评价指标

2.7.2 切分训练数据和线下验证数据

# 采用 pca 保留16维特征的数据
train_data = np.load('./train_data_pca.npz')['X_train']
target_data = np.load('./train_data_pca.npz')['y_train']

# 切分数据 训练数据80% 验证数据20%
X_train,X_valid,y_train,y_valid=train_test_split(train_data,target_data,
                                                               test_size=0.2)

2.7.3 多元线性回归模型

clf = LinearRegression()
clf.fit(X_train, y_train)
score = mean_squared_error(y_valid, clf.predict(X_valid))
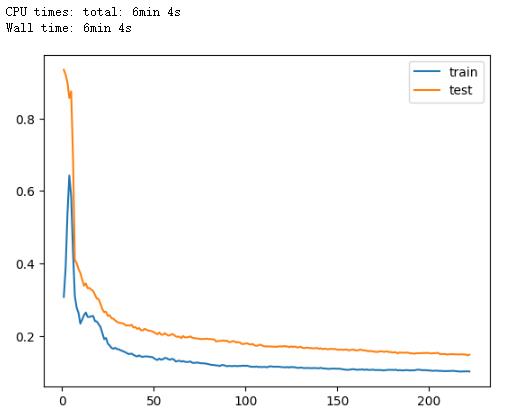
print("LinearRegression:   ", score)    # LinearRegression:    0.10432848181938673

2.7.4 训练数据验证数据评估可视化

def plot_learning_curve(model, X_train, X_valid, y_train, y_valid):
    '绘制学习曲线：只需要传入算法(或实例对象)、X_train、X_valid、y_train、y_valid'
    train_score = []
    valid_score = []
    
    for i in range(10, len(X_train)+1, 10):
        model.fit(X_train[:i], y_train[:i])
        # 训练数据评估
        y_train_predict = model.predict(X_train[:i])
        train_score.append(mean_squared_error(y_train[:i], y_train_predict))
        
        # 验证数据评估
        y_valid_predict = model.predict(X_valid)
        valid_score.append(mean_squared_error(y_valid, y_valid_predict))
    
    # 可视化
    plt.plot([i for i in range(1, len(train_score)+1)],
            train_score, label="train")
    plt.plot([i for i in range(1, len(valid_score)+1)],
            valid_score, label="test")
    plt.legend()

plot_learning_curve(LinearRegression(), X_train, X_valid, y_train, y_valid)
plt.savefig('./9-多元线性回归训练验证数据评估对比.png',dpi = 200)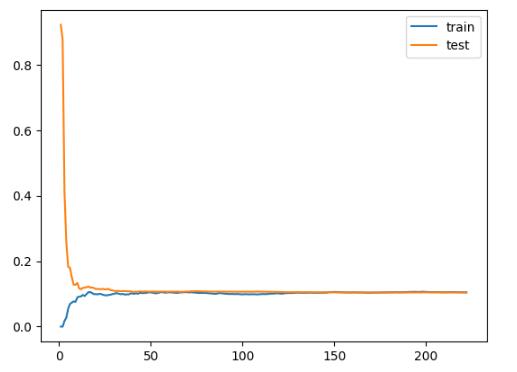

2.7.5 K近邻回归

for i in range(3,20):
    clf = KNeighborsRegressor(n_neighbors=i) # 最近三个
    clf.fit(X_train, y_train)
    score = mean_squared_error(y_valid, clf.predict(X_valid))
    print("KNeighborsRegressor:   ", score)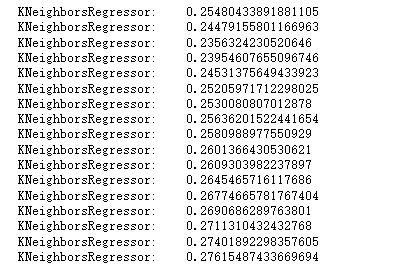

2.7.6 决策树回归

clf = DecisionTreeRegressor() 
clf.fit(X_train, y_train)
score = mean_squared_error(y_valid, clf.predict(X_valid))
print("DecisionTreeRegressor:",score)  # DecisionTreeRegressor: 0.2640828671454219

2.7.7 随机森林回归

clf = RandomForestRegressor(n_estimators=200, # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',# 构建树时，特征筛选量
                            min_samples_leaf=10,# 是叶节点所需的最小样本数
                            min_samples_split=40,# 是分割所需的最小样本数
                            criterion='squared_error')
clf.fit(X_train, y_train)
score = mean_squared_error(y_valid, clf.predict(X_valid))
print("RandomForestRegressor: ", score)    # RandomForestRegressor: 0.14848566312

%%time
clf = RandomForestRegressor(n_estimators=200,        # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',   # 构建树时，特征筛选量
                            min_samples_leaf=10,     # 是叶节点所需的最小样本数
                            min_samples_split=40,    # 是分割所需的最小样本数
                            criterion='squared_error')
plot_learning_curve(clf, X_train, X_valid, y_train, y_valid)

2.7.8 SVR支持向量机

clf1 = SVR(kernel='rbf',C = 1,gamma=0.01,tol = 0.0001,epsilon=0.3)
clf1.fit(X_train, y_train)
score = mean_squared_error(y_valid, clf1.predict(X_valid))
print("支持向量机高斯核函数:   ", score)      # 0.09906820170848413
clf2 = SVR(kernel='poly')
clf2.fit(X_train, y_train)
score = mean_squared_error(y_valid, clf2.predict(X_valid))
print("支持向量机多项式核函数:   ", score)    # 0.23220958170673037

C：表示错误项的惩罚系数C越大，即对分错样本的惩罚程度越大，因此在训练样本中准确率越高，但是泛化能力降低；相反，减小C的话，容许训练样本中有一些误分类错误样本，泛化能力强。对于训练样本带有噪声的情况，一般采用后者，把训练样本集中错误分类的样本作为噪声。
gamma：‘rbf’, ‘poly’ 和‘sigmoid’ 核函数的系数
epsilon:

• 1. 用来定义模型对于错误分类的容忍度，即错误分类而不受到惩罚
• 2. epsilon的值越大，模型允许错误分类的容忍度越高，反之，容忍度越小
• 3. 支持向量的个数对 epsilon的大小敏感，即 epsilon的值越大，支持向量的个数越少，反之，支持向量的个数越多
• 4. 也可以理解为epsilon的值越小，模型越过拟合，反之，越大越欠拟合

plot_learning_curve(clf1,X_train, X_valid, y_train, y_valid)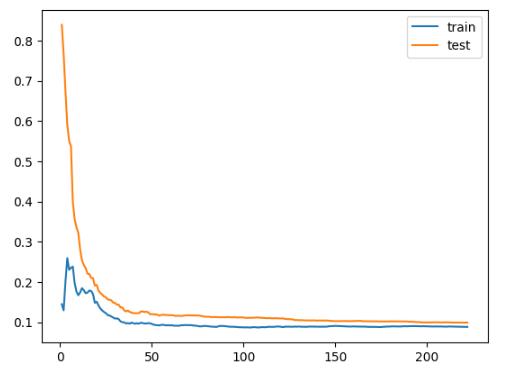

 2.7.9 lightGBM

clf = lgb.LGBMRegressor(learning_rate=0.05, # 学习率
                        n_estimators=300,# 集成树数量
                        min_child_samples=10,# 是叶节点所需的最小样本数
                        max_depth=5, # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,#构建树时特征选择比例
                        subsample=0.8,# 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
clf.fit(X_train, y_train)
score = mean_squared_error(y_valid, clf.predict(X_valid))
print("LGB模型均方误差:   ", score)       # 0.10190918545761905

• min_child_samples: 一个叶子上的最小数据量。默认设置为20。根据数据量来确定，当数据量比较大时，应该提升这个数值，让叶子节点的数据分布相对稳定，提高模型的泛华能力。max_depth: 树模型的最大深度。防止过拟合的最重要的参数，一般限制为3~5之间。是需要调整的核心参数，对模型性能和泛化能力有决定性作用。
• num_leaves:一棵树上的叶子节点个数。默认设置为31，和max_depth配合来空值树的形状，一般设置为(0, 2^max_depth - 1]的一个数值。是一个需要重点调节的参数，对模型性能影响很大。
• reg_alpha: L1正则化参数，别名：lambda_l1。默认设置为0。一般经过特征选择后这个参数不会有特别大的差异，如果发现这个参数数值大，则说明有一些没有太大作用的特征在模型内。需要调节来控制过拟合。
• reg_lambda: L2正则化参数，别名：lambda_l2。默认设置为0。较大的数值会让各个特征对模型的影响力趋于均匀，不会有单个特征把持整个模型的表现。需要调节来控制过拟合

2.7.10 Gradient Boosting

%%time
clf = GradientBoostingRegressor(learning_rate=0.03, # 学习率
                                loss='huber',  # 损失函数
                                max_depth=14, # 决策树深度
                                max_features='sqrt',# 节点分裂时参与判断的最大特征数
                                min_samples_leaf=10,# 是叶节点所需的最小样本数
                                min_samples_split=40,# 是分割所需的最小样本数
                                n_estimators=300,# 集成树数量
                                subsample=0.8)# 抽样比例
clf.fit(X_train, y_train)
score = mean_squared_error(y_valid, clf.predict(X_valid))
print("GradientBoostingRegressor:   ", score)   # 0.09975389216573424

参数说明：例如，如果min_sample_split = 6并且节点中有4个样本，则不会发生拆分（不管熵是多少）；假设min_sample_leaf = 3并且一个含有5个样本的节点可以分别分裂成2个和3个大小的叶子节点，那么这个分裂就不会发生，因为最小的叶子大小为3 .
损失函数loss：

• squared_error：均方误差
• absolute_error：绝对损失
• huber：上面两者融合

K近邻算法、决策树回归表现比较差, 多元线性回归有待后续继续验证（存在过拟合情况）

---

第三部分 模型预测

3.1 导入相应算法

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression  #线性回归
from sklearn.ensemble import RandomForestRegressor #随机森林回归
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.svm import SVR  #支持向量回归
import lightgbm as lgb #lightGbm模型
from xgboost import XGBRFRegressor
from sklearn.model_selection import train_test_split # 切分数据
from sklearn.metrics import mean_squared_error #评价指标

from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
import warnings
warnings.filterwarnings('ignore')

3.2 加载数据

3.2.1 未降维数据

all_data = pd.read_csv('./processed_zhengqi_data2.csv')
# 训练数据
cond = all_data['label'] == 'train'
train_data = all_data[cond]
train_data.drop(labels = 'label',axis = 1,inplace = True)
# 切分数据 训练数据80% 验证数据20%
X_train,X_valid,y_train,
y_valid=train_test_split(train_data.drop(labels='target',axis = 1),
                                                 train_data['target'],
                                                 test_size=0.2)
# 测试数据
cond2 = all_data['label'] == 'test'
test_data = all_data[cond2]
test_data.drop(labels = ['label','target'],axis = 1,inplace = True)
all_data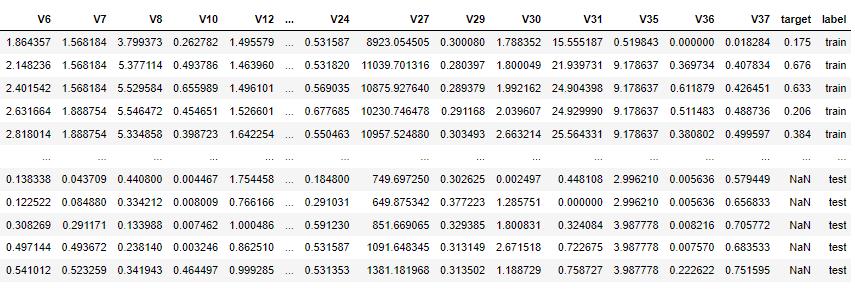

 3.2.2 降维数据

#采用 pca 保留特征的数据
train_data_pca = np.load('./train_data_pca.npz')['X_train']
target_data_pca = np.load('./train_data_pca.npz')['y_train']

# 切分数据 训练数据80% 验证数据20%
X_train_pca,X_valid_pca,y_train_pca,
y_valid_pca=train_test_split(train_data_pca,target_data_pca, test_size=0.2)
test_data_pca = np.load('./test_data_pca.npz')['X_test']
train_data_pca.shape      # (2784, 22)

3.3 定义绘制模型学习曲线函数

def plot_learning_curve(model,title,X,y,cv=None):
    
    # 学习曲线计算
    train_sizes, train_scores, test_scores = learning_curve(model, X, y, cv=cv)
    print(train_sizes,train_scores.shape,test_scores.shape)
    
    # 训练数据得分和测试数据得分平均值与方差计算
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    
    # 训练数据得分可视化
    plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
             label="Training score")
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
                     train_scores_mean + train_scores_std, alpha=0.1,color="r")
    
    # 测试数据得分可视化
    plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
             label="Cross-validation score")
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
                     test_scores_mean + test_scores_std, alpha=0.1, color="g")
    # 画图设置
    plt.grid() # 网格线设置
    plt.legend(loc="best") # 图例设置
    # 标题标签设置
    plt.title(title)
    plt.xlabel("Training examples")
    plt.ylabel("Score")

3.4 多元线性回归模型

3.4.1 模型训练

降维数据建模验证:

clf = LinearRegression()
clf.fit(X_train_pca, y_train_pca)
clf.score(X_train_pca, y_train_pca)    # 0.885517101140185

未降维数据建模验证:

clf = LinearRegression()
clf.fit(X_train, y_train)
clf.score(X_train, y_train)     # 0.8893207806471845

3.4.2  绘制线性回归模型学习曲线

学习曲线是不同训练集大小，模型在训练集和验证集上的得分变化曲线。也就是以样本数为横坐标，训练和交叉验证集上的得分（如准确率）为纵坐标。  
learning curve可以帮助我们判断模型现在所处的状态：

• 过拟合（overfiting / high variance 高方差）:  说明模型能够很好的拟合已知数据，但是泛化能力很差，属于高方差
• 欠拟合（underfitting / high bias 高偏差）:  这说明模拟对已知数据和未知都不能进行准确的预测，属于高偏差

X = X_train_pca
y = y_train_pca
# 多元线性回归模型学习曲线图
title = "LinearRegression"

cv = ShuffleSplit(n_splits=100, test_size=0.25)
estimator = LinearRegression()      # 建模
plot_learning_curve(estimator, title, X, y, cv = cv)
plt.savefig('./10-多元线性回归降维数据学习曲线.png',dpi = 200)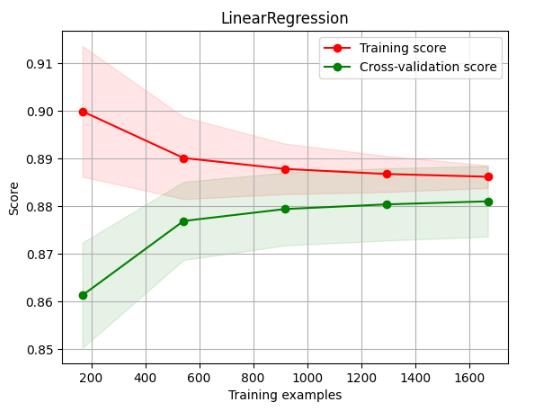

X = X_train
y = y_train
# 多元线性回归模型学习曲线图
title = "LinearRegression"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
estimator = LinearRegression()      # 建模
plot_learning_curve(estimator, title, X, y, cv = cv)
plt.savefig('./11-多元线性回归非降维数据学习曲线.png',dpi = 200)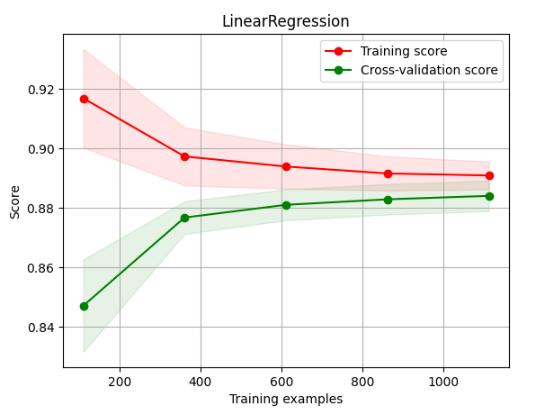

 3.4.3 模型预测

降维数据建模预测 :

# 得分是：0.1598
model = LinearRegression()
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)   # array([ 0.18802274,  0.24611291, ...,-2.23076209])
np.savetxt('./多元线性回归模型预测(降维数据).txt',y_)

非降维数据建模预测 :

# 得分是：0.1620
model = LinearRegression()
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)    # array([ 0.180302  ,  0.21599399, -0.17268982, ..., -2.06587572])
np.savetxt('./多元线性回归模型预测(非降维数据).txt',y_)

3.5 随机森林模型建模

3.5.1  模型训练

降维数据建模验证

model = RandomForestRegressor(n_estimators=200,    # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto', # 构建树时，特征筛选量
                            min_samples_leaf=10,   # 是叶节点所需的最小样本数
                            min_samples_split=40,  # 是分割所需的最小样本数
                            criterion='squared_error')
model.fit(X_train_pca, y_train_pca)
score = mean_squared_error(y_valid_pca, model.predict(X_valid_pca))
print("随机森林得分:   ", score)    # 0.1535330953946485

非降维数据建模验证

model = RandomForestRegressor(n_estimators=200, # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',# 构建树时，特征筛选量
                            min_samples_leaf=10,# 是叶节点所需的最小样本数
                            min_samples_split=40,# 是分割所需的最小样本数
                            criterion='squared_error')
model.fit(X_train, y_train)
score = mean_squared_error(y_valid, model.predict(X_valid))
print("随机森林得分:   ", score)     # 0.10046589910006855

3.5.2  绘制学习曲线

绘制学习曲线比较耗时间，这里绘制非降维数据的学习曲线

%%time
X = X_train
y = y_train
# 随机森林模型学习曲线图
title = "RandomForestRegressor"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
model = RandomForestRegressor(n_estimators=200, # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',# 构建树时，特征筛选量
                            min_samples_leaf=10,# 是叶节点所需的最小样本数
                            min_samples_split=40,# 是分割所需的最小样本数
                            criterion='squared_error')
plot_learning_curve(model, title, X, y, cv = cv)
plt.savefig('./12-随机森林非降维数据学习曲线.png',dpi = 200)

3.5.3  模型预测

降维数据建模预测

# 得分是：1.0579
model =  RandomForestRegressor(n_estimators=200, # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',# 构建树时，特征筛选量
                            min_samples_leaf=10,# 是叶节点所需的最小样本数
                            min_samples_split=40,# 是分割所需的最小样本数
                            criterion='squared_error')
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./随机森林模型预测(降维数据).txt',y_)

# 得分是：0.1461
model = RandomForestRegressor(n_estimators=200, # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',# 构建树时，特征筛选量
                            min_samples_leaf=10,# 是叶节点所需的最小样本数
                            min_samples_split=40,# 是分割所需的最小样本数
                            criterion='squared_error')
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./随机森林模型预测(非降维数据).txt',y_)

3.6  SVR支持向量机

3.6.1  模型训练

降维数据

model = SVR(kernel='rbf',C = 1,gamma=0.01,tol = 0.0001,epsilon=0.3)
model.fit(X_train_pca, y_train_pca)
model.score(X_train_pca, y_train_pca)    # 0.9050979451452323

非降维数据

model = SVR(kernel='rbf')
model.fit(X_train, y_train)
# score = mean_squared_error(y_valid, model.predict(X_valid))
# print("SVR支持向量机得分:   ", score)
model.score(X_train, y_train)    # 0.7340096725801917

3.6.2  绘制学习曲线

降维数据

%%time
X = X_train_pca
y = y_train_pca
# 随机森林模型学习曲线图
title = "SVR"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
model = SVR(kernel='rbf',C = 1,gamma=0.01,tol = 0.0001,epsilon=0.3)
plot_learning_curve(model, title, X, y, cv = cv)
plt.savefig('./15-SVR降维数据学习曲线.png',dpi = 200)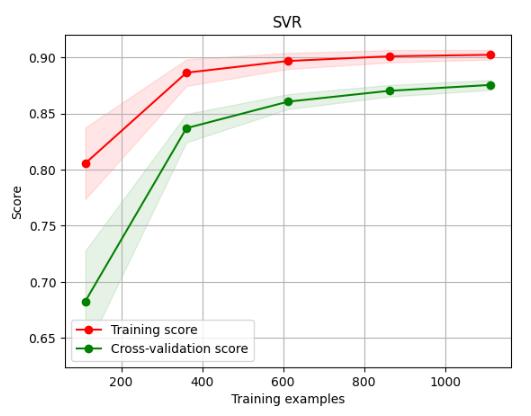

非降维数据

%%time
X = X_train
y = y_train
# 随机森林模型学习曲线图
title = "SVR"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
model = SVR(kernel='rbf')
plot_learning_curve(model, title, X, y, cv = cv)
plt.savefig('./16-SVR非降维数据学习曲线.png',dpi = 200)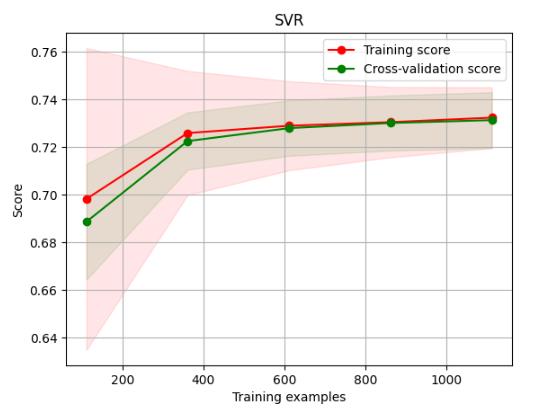

 3.6.3  模型预测

降维数据

# 得分是：0.2654
model =  SVR(kernel='rbf',C = 1,gamma=0.01,tol = 0.0001,epsilon=0.3)
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./SVR模型预测(降维数据).txt',y_)  # array([ 0.26958642,...,-2.18865886])

非降维数据

# 得分是：1.9934
model =SVR(kernel='rbf')
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./SVR模型预测(非降维数据).txt',y_)  #array([ 0.02366046,...,-3.10625782])

poly多项式核函数建模预测--降维数据

# 得分是：4.7068
model =  SVR(kernel='poly')
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./SVR-poly预测(降维数据).txt',y_) # array([0.20042313,...,-2.76923448])

poly多项式核函数建模预测--非降维数据

# 得分是：0.7423
model =SVR(kernel='poly')
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./SVR-poly模型(非降维).txt',y_)  # array([-0.07224459,...,-0.45593334])

3.7  GBDT梯度提升树

3.7.1  模型训练

降维数据

model = GradientBoostingRegressor(learning_rate=0.03, # 学习率
                                loss='huber',  # 损失函数
                                max_depth=14, # 决策树深度
                                max_features='sqrt',# 节点分裂时参与判断的最大特征数
                                min_samples_leaf=10,# 是叶节点所需的最小样本数
                                min_samples_split=40,# 是分割所需的最小样本数
                                n_estimators=300,# 集成树数量
                                subsample=0.8)# 抽样比例
model.fit(X_train_pca, y_train_pca)
model.score(X_train_pca, y_train_pca)   # 0.987028196530497

非降维数据

model = GradientBoostingRegressor(learning_rate=0.03, # 学习率
                                loss='huber',  # 损失函数
                                max_depth=14, # 决策树深度
                                max_features='sqrt',# 节点分裂时参与判断的最大特征数
                                min_samples_leaf=10,# 是叶节点所需的最小样本数
                                min_samples_split=40,# 是分割所需的最小样本数
                                n_estimators=300,# 集成树数量
                                subsample=0.8)# 抽样比例
model.fit(X_train, y_train)
# score = mean_squared_error(y_valid, model.predict(X_valid))
# print("GBDT得分:   ", score)
model.score(X_train, y_train)    # 0.9882808230330608

3.7.2 绘制学习曲线

降维数据学习曲线

%%time
X = X_train_pca
y = y_train_pca
# 随机森林模型学习曲线图
title = "GBDT"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
model = GradientBoostingRegressor(learning_rate=0.03, # 学习率
                                loss='huber',  # 损失函数
                                max_depth=14, # 决策树深度
                                max_features='sqrt',# 节点分裂时参与判断的最大特征数
                                min_samples_leaf=10,# 是叶节点所需的最小样本数
                                min_samples_split=40,# 是分割所需的最小样本数
                                n_estimators=300,# 集成树数量
                                subsample=0.8)# 抽样比例
plot_learning_curve(model, title, X, y, cv = cv)
plt.savefig('./17-GBDT降维数据学习曲线.png',dpi = 200)

3.7.3  模型预测

降维数据

# 得分是：0.3765
model =  GradientBoostingRegressor(learning_rate=0.03, # 学习率
                                loss='huber',  # 损失函数
                                max_depth=14, # 决策树深度
                                max_features='sqrt',# 节点分裂时参与判断的最大特征数
                                min_samples_leaf=10,# 是叶节点所需的最小样本数
                                min_samples_split=40,# 是分割所需的最小样本数
                                n_estimators=300,# 集成树数量
                                subsample=0.8)# 抽样比例
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./GBDT模型预测(降维数据).txt',y_)

非降维数据

# 得分是：0.1392
model = GradientBoostingRegressor(learning_rate=0.03, # 学习率
                                loss='huber',  # 损失函数
                                max_depth=14, # 决策树深度
                                max_features='sqrt',# 节点分裂时参与判断的最大特征数
                                min_samples_leaf=10,# 是叶节点所需的最小样本数
                                min_samples_split=40,# 是分割所需的最小样本数
                                n_estimators=300,# 集成树数量
                                subsample=0.8)# 抽样比例
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./GBDT模型预测(非降维数据).txt',y_)

3.8  lightGBM

3.8.1  模型训练

降维数据

model = lgb.LGBMRegressor(learning_rate=0.05, # 学习率
                        n_estimators=300,# 集成树数量
                        min_child_samples=10,# 是叶节点所需的最小样本数
                        max_depth=5, # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,#构建树时特征选择比例
                        subsample=0.8,# 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
model.fit(X_train_pca, y_train_pca)
# score = mean_squared_error(y_valid_pca, model.predict(X_valid_pca))
# print("LGB得分:   ", score)
model.score(X_train_pca, y_train_pca)  # 0.9785680162426776

非降维数据

model = lgb.LGBMRegressor(learning_rate=0.05, # 学习率
                        n_estimators=300,# 集成树数量
                        min_child_samples=10,# 是叶节点所需的最小样本数
                        max_depth=5, # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,#构建树时特征选择比例
                        subsample=0.8,# 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
model.fit(X_train, y_train)
# score = mean_squared_error(y_valid, model.predict(X_valid))
# print("LGB得分:   ", score)
model.score(X_train, y_train)   # 0.9794375108491288

3.8.2  绘制学习曲线

降维数据

%%time
X = X_train
y = y_train
# lightGBM模型学习曲线图
title = "lightGBM"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
model = lgb.LGBMRegressor(learning_rate=0.05, # 学习率
                        n_estimators=300,# 集成树数量
                        min_child_samples=10,# 是叶节点所需的最小样本数
                        max_depth=5, # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,#构建树时特征选择比例
                        subsample=0.8,# 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
plot_learning_curve(model, title, X, y, cv = cv)
plt.savefig('./22-lightGBM非降维数据学习曲线.png',dpi = 200)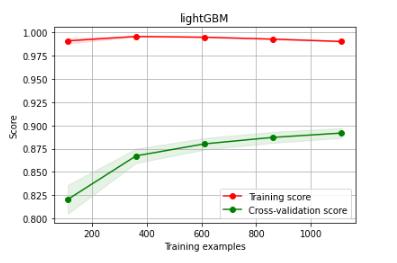

 3.8.3  模型预测

降维数据

# 得分是：0.6383
model =  lgb.LGBMRegressor(learning_rate=0.05, # 学习率
                        n_estimators=100,# 集成树数量
                        min_child_samples=10,# 是叶节点所需的最小样本数
                        max_depth=5, # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,#构建树时特征选择比例
                        subsample=0.8,# 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./lightGBM模型预测(降维数据).txt',y_)

非降维数据

# 得分是：0.1378
model = lgb.LGBMRegressor(learning_rate=0.05,   # 学习率
                        n_estimators=100,       # 集成树数量
                        min_child_samples=10,   # 是叶节点所需的最小样本数
                        max_depth=5,  # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,  # 构建树时特征选择比例
                        subsample=0.8,  # 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./lightGBM模型预测(非降维数据).txt',y_)

3.9  Xgboost

3.9.1  模型训练

降维数据

model = XGBRFRegressor(n_estimators = 300, 
                       max_depth=15,
                       subsample = 0.8,
                       colsample_bytree = 0.8,
                       learning_rate =1,
                       gamma = 0,
                       reg_lambda= 0 ,# L2正则化
                       reg_alpha = 0,verbosity=1)# L1正则化
model.fit(X_train_pca, y_train_pca)
score = model.score(X_train_pca, y_train_pca)
# score = mean_squared_error(y_valid_pca, model.predict(X_valid_pca))
print("Xgboost得分:   ", score)  # Xgboost得分: 0.9884996208639248

非降维数据

model = XGBRFRegressor(n_estimators = 300, 
                       max_depth=15,
                       subsample = 0.8,
                       colsample_bytree = 0.8,
                       learning_rate =1,
                       gamma = 0,
                       reg_lambda= 0 ,# L2正则化
                       reg_alpha = 0,verbosity=1)# L1正则化
model.fit(X_train, y_train)
score = model.score(X_train, y_train)
# score = mean_squared_error(y_valid, model.predict(X_valid))
print("Xgboost得分: ", score)  # Xgboost得分: 0.9947476702889748

3.9.2  模型预测

降维数据

# 得分是：0.6798
model = XGBRFRegressor(n_estimators = 300, 
                       max_depth=15,
                       subsample = 0.8,
                       colsample_bytree = 0.8,
                       learning_rate =1,
                       gamma = 0,
                       reg_lambda= 0 ,    # L2正则化
                       reg_alpha = 0,verbosity=1)  # L1正则化
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./Xgboost预测(降维).txt',y_)  # array([
以上是关于02- 天池工业蒸汽量项目实战 (项目二)的主要内容，如果未能解决你的问题，请参考以下文章
 
 Python工业项目实战：服务器性能监控Prometheus及项目总结
 Python工业项目实战02：数仓设计及数据采集
 智能制造概念
 大数据,云计算,数据挖掘实战，实时推荐系统实战，电视收视率项目实战，实时流统计项目实战视频教程
 秒杀系统企业级实战应用之真实工业界案例
 工业监控项目实战1—UI