算法教程

Posted 2023-02-25 喵喵喵爱吃鱼

自学算法第二章

本章课程承接作者主页中《自学算法》的第一章内容。

这套课程特别适合自学算法的小白。每节课程最后还有一道练习题，边学边练，可以帮你及时巩固学习到的知识。

如果您在学习其他相关的算法课程，也可以学习该课程用来巩固知识点。

本教程中的练习题，请移步 1024乐学编程-算法基础 进行练习。

您也可以在该网站免费学习到更多课程

数据结构

数据结构，直白地理解，就是研究数据的存储方式。在处理问题的时候，经常需要先将一些数据进行储存，然后，通过算法进行解决。
用不同的方式储存数据，就会占用大小不等的存储空间，同时，用算法处理的时候，处理的过程也就会有些许的不同。所以，储存数据的方式也主要是为了能够配合算法实现目标。

栈

数据结构大致包含以下几种存储结构：
线性表，还可细分为顺序表、链表、栈和队列；
树结构，包括普通树，二叉树，线索二叉树等；
图存储结构；

接下来我们先说说线性表中的栈。

栈是用来存储逻辑关系为 "一对一" 数据的线性存储结构

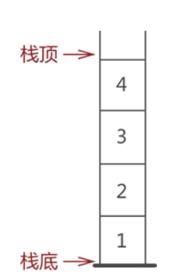
栈只能从表的一端存取数据，另一端是封闭的，如图所示；
在栈中，无论是存数据还是取数据，都必须遵循"先进后出"的原则，即最先进栈的元素最后出栈。拿图中的栈来说，从图中数据的存储状态可判断出，元素 1 是最先进的栈。因此，当需要从栈中取出元素 1 时，根据"先进后出"的原则，需提前将元素 3 和元素 2 从栈中取出，然后才能成功取出元素 1。
因此，我们可以给栈下一个定义，即栈是一种只能从表的一端存取数据且遵循 "先进后出" 原则的线性存储结构。

通常，栈的开口端被称为栈顶；相应地，封口端被称为栈底。因此，栈顶元素指的就是距离栈顶最近的元素，如图，栈顶元素为元素 4；同理，栈底元素指的是位于栈最底部的元素，图 中的栈底元素为元素 1。

进栈和出栈

基于栈结构的特点，在实际应用中，通常只会对栈执行以下两种操作：
▶向栈中添加元素，此过程被称为"进栈"（入栈或压栈）；
▶从栈中提取出指定元素，此过程被称为"出栈"（或弹栈）；

栈的应用

基于栈结构对数据存取采用 "先进后出" 原则的特点，它可以用于实现很多功能。
例如，我们经常使用浏览器在各种网站上查找信息。假设先浏览的页面 A，然后关闭了页面 A 跳转到页面 B，随后又关闭页面 B 跳转到了页面 C。而此时，我们如果想重新回到页面 A，有两个选择：
▶ 重新搜索找到页面 A；
▶ 使用浏览器的"回退"功能。浏览器会先回退到页面 B，而后再回退到页面 A。

浏览器 "回退" 功能的实现，底层使用的就是栈存储结构。当你关闭页面 A 时，浏览器会将页面 A 入栈；同样，当你关闭页面 B 时，浏览器也会将 B入栈。因此，当你执行回退操作时，才会首先看到的是页面 B，然后是页面 A，这是栈中数据依次出栈的效果。

不仅如此，栈存储结构还可以帮我们检测代码中的括号匹配问题。多数编程语言都会用到括号（小括号、中括号和大括号），括号的错误使用（通常是丢右括号）会导致程序编译错误，而很多开发工具中都有检测代码是否有编辑错误的功能，其中就包含检测代码中的括号匹配问题，此功能的底层实现使用的就是栈结构。

同时，栈结构还可以实现数值的进制转换功能。例如，编写程序实现从十进制数自动转换成二进制数，就可以使用栈存储结构来实现。

以上也仅是栈应用领域的冰山一角，接下来我们介绍栈的基本操作

入栈

在顺序表中设定一个实时指向栈顶元素的变量（一般命名为 top），top 初始值为 -1，表示栈中没有存储任何数据元素，及栈是"空栈"。一旦有数据元素进栈，则 top 就做 +1 操作；反之，如果数据元素出栈，top 就做 -1 操作。
模拟栈存储 1,2,3,4 的过程。最初，栈是"空栈"，即数组是空的，top 值为初始值 -1，如下

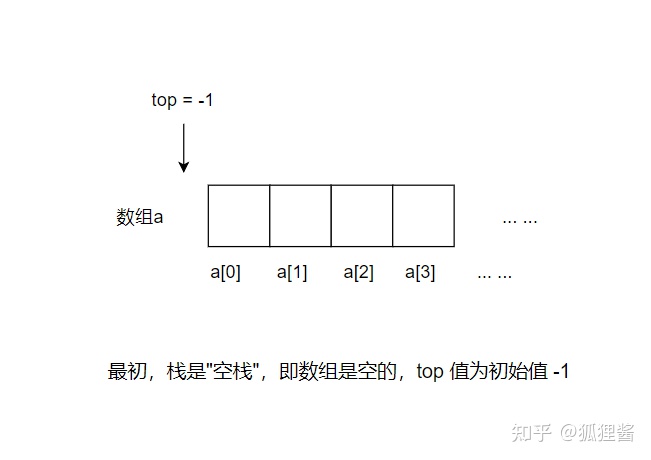
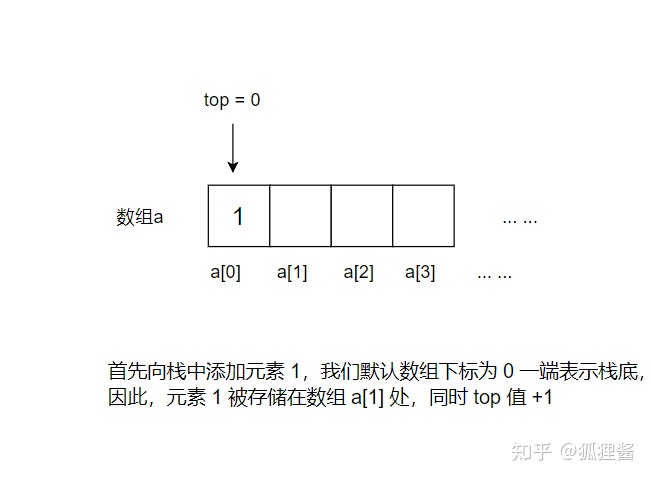
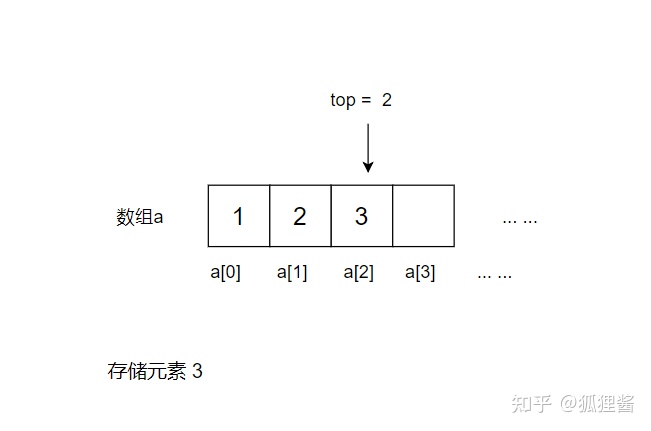
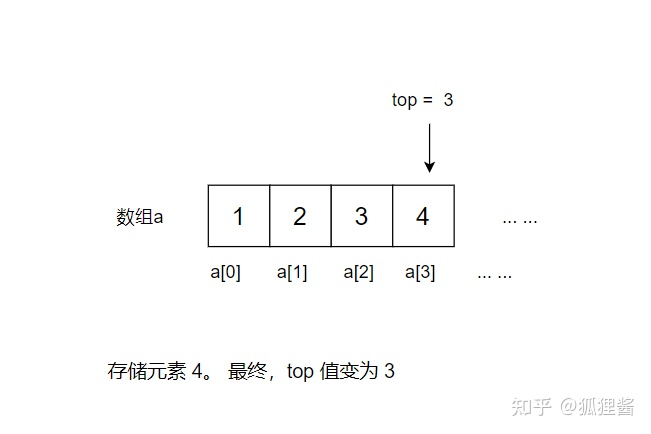
图5

出栈

其实，top 变量的设置对模拟数据的 "入栈" 操作没有实际的帮助，它是为实现数据的 "出栈" 操作做准备的。

比如，将图 5 中的元素 2 出栈，则需要先将元素 4 和元素 3 依次出栈。需要注意的是，当有数据出栈时，要将 top 做 -1 操作。因此，元素 4 和元素 3 出栈的过程如下流程图

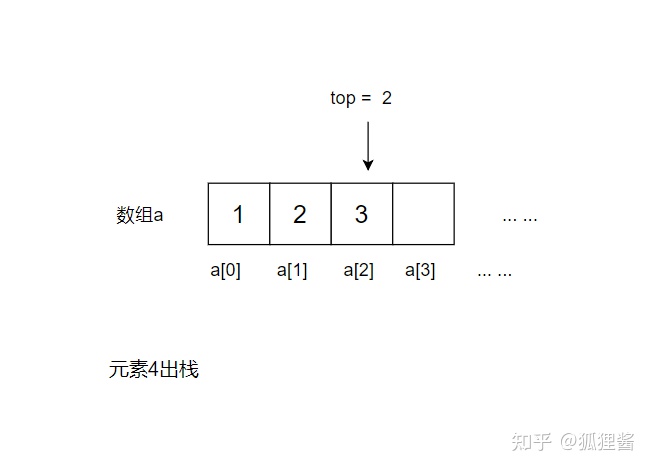
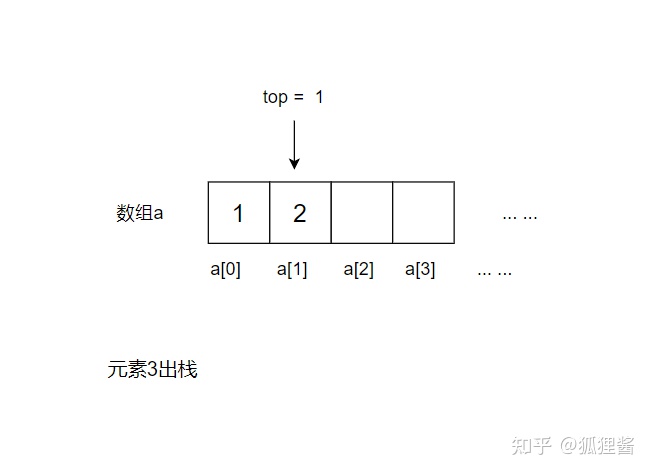
代码

元素 4 和元素 3 全部出栈后，元素 2 才能出栈。
通过学习顺序表模拟栈中数据入栈和出栈的操作，初学者完成了对顺序栈的学习，这里给出顺序栈及对数据基本操作的代码：

#include <iostream>
using namespace std;
int push(int* a , int top , int elem) //元素elem进栈
    a[ ++top ] = elem;
 return top;

int pop(int * a , int top)//数据元素出栈
 if (top == -1) 
        cout << "空栈";
 return -1;
 
    cout << "弹栈元素："<< a[ top ] << endl;
    top--;
 return top;

int main() 
 int a[100];
 int top = -1;
    top = push(a, top, 1);
    top = push(a, top, 2);
    top = push(a, top, 3);
    top = push(a, top, 4);
    top = pop(a, top);
    top = pop(a, top);
    top = pop(a, top);
    top = pop(a, top);
    top = pop(a, top);
 return 0;

程序输出结果为：

弹栈元素：4
弹栈元素：3
弹栈元素：2
弹栈元素：1
空栈

回文字符串

接下来咱们做个练习，“xyzyx”是一个回文字符串，回文字符串就是指正读反读均相同的字符序列， 如“席主席”、“记书记”、“aha”和“ahaha”均是回文， 但“ahah”不是回文。通过栈这个数据结构我们将很容易判断一个字符串是否为回文。
首先我们需要读取这行字符串，并求出这个字符串的长度。

string a ;
cin >> a; //读入一行字符串
int len = a.length(); //求字符串的长度

如果一个字符串是回文的话，那么它必须是中间对称的，我们需要求中点，即

int mid=len/2-1; //求字符串的中点

接下来就轮到栈出场了

我们先将mid之前的字符全部入栈。因为这里的栈是用来存储字符的， 所以这里用来实现栈的数组类型是字符数组即chars[101] ； ， 初始化栈很简单， top=0； 就可以了。入栈的操作是 top++; s[top] = x (假设需要入栈的字符暂存在字符变量x中)， 其实可以简写为s[++top] -x;
现在我们就来将mid之前的字符依次全部入栈。

for(i=0; i <= mid; i++)
        s[ ++top ] = a[ i ] ;
    

接下来进入判断回文的关键步骤。将当前栈中的字符依次出栈， 看看是否能与mid方的字符一一匹配，如果都能匹配则说明这个字符串是回文字符串，否则这个字符串就不是回文字符串。

 //开始匹配
 for(i = next; i <= len-1; i++)
 if(a[ i ] !=s[ top ])
 break;
 
        top-- ;
 
 //如果top的值为0， 则说明栈内所有的字符都被一一匹配了
 if( top == 0 )
    cout << "YES";
 else
    cout << "NO";

做一道练习题，请移步到该网站的算法基础课程中，《栈》的小节，习题在内容最后。

http://www.eluzhu.com:1818/my/course/65

队列

这节课我们学习与栈相反，“先进先出”的队列。
队列（queue）是一种具有「先进入队列的元素一定先出队列」性质的表。由于该性质，队列通常也被称为先进先出（first in first out）表，简称 FIFO 表。
队列，和栈一样，也是一种对数据的"存"和"取"有严格要求的线性存储结构。
与栈结构不同的是，队列的两端都"开口"，要求数据只能从一端进，从另一端出，如图

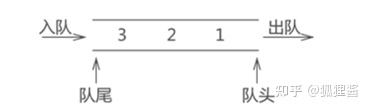
通常，称进数据的一端为 "队尾"，出数据的一端为 "队头"，数据元素进队列的过程称为 "入队"，出队列的过程称为 "出队"。
不仅如此，队列中数据的进出要遵循 "先进先出" 的原则，即最先进队列的数据元素，同样要最先出队列。拿图中的队列来说，从数据在队列中的存储状态可以分析出，元素 1 最先进队，其次是元素 2，最后是元素 3。此时如果将元素 3 出队，根据队列 "先进先出" 的特点，元素 1 要先出队列，元素 2 再出队列，最后才轮到元素 3 出队列。
栈和队列不要混淆，栈结构是一端封口，特点是"先进后出"；而队列的两端全是开口，特点是"先进先出"。

顺序队列简单实现

由于顺序队列的底层使用的是数组，因此需预先申请一块足够大的内存空间初始化顺序队列。除此之外，为了满足顺序队列中数据从队尾进，队头出且先进先出的要求，我们还需要定义两个指针（top 和 rear）分别用于指向顺序队列中的队头元素和队尾元素，如图

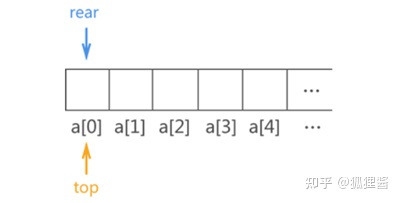
由于顺序队列初始状态没有存储任何元素，因此 top 指针和 rear 指针重合，且由于顺序队列底层实现靠的是数组，因此 top 和 rear 实际上是两个变量，它的值分别是队头元素和队尾元素所在数组位置的下标。

当有数据元素进队列时，对应的实现操作是将其存储在指针 rear 指向的数组位置，然后 rear+1；当需要队头元素出队时，仅需做 top+1 操作。
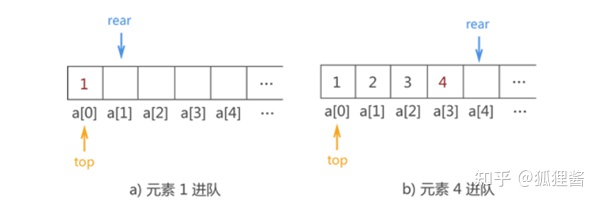
例如，将 1,2,3,4 用顺序队列存储的实现操作如图所示：

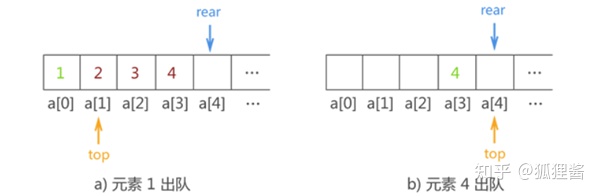
顺序队列中数据出队列的实现过程如下图所示：

因此，使用顺序表实现顺序队列最简单方法的实现代码为：

#include <iostream>
using namespace std;
int enQueue( int *a, int rear, int data )
    a[ rear ] =  data;
    rear++;
 return rear;

void deQueue( int *a, int front, int rear )
 while (front  != rear)//如果 front == rear，表示队列为空
        cout << "出队元素:" <<  a[ front ] << endl;
        front++;
 

int main( )
 int a[ 100 ];
 int front, rear;
 //设置队头指针和队尾指针，当队列中没有元素时，队头和队尾指向同一块地址
    front = rear = 0;
    rear = enQueue(a, rear, 1);//入队
    rear = enQueue(a, rear, 2);
    rear = enQueue(a, rear, 3);
    rear = enQueue(a, rear, 4);
 deQueue(a, front, rear);//出队
 return 0;

练习题

下面我们做一道练习题，有一组加密后的密码 631758924，需要进行解密，规则是这样的：首先将第1个数删除，紧接着将第2个数放到这串数的末尾，再将第3个数删除并将第4个数放到这串数的末尾，再将第5个数删除……
直到剩下最后一个数，将最后一个数也删除。按照刚才删除的顺序，把这些删除的数连在一起就是我们最后得到的密码啦。

我来试试，刚开始这串数是“6 3 1 7 5 8 9 2 4”，首先删除6并将3放到这串数的末尾，这串数更新为“17589243”。接下来删除1并将7放到末尾，即重新为“5 8 9 2 4 3 7”。再删除5并将8放到末尾即“9 2 4 3 7 8”，删除9并将2放到末尾即“4 3 7 8 2"，删除4并将3放到末尾即“7 8 2 3”，删除7并将8放到末尾即“2 3 8”，删除2并将3放到末尾即“83”，删除8并将3放到末尾即“3”，最后删除3。因此被删除的顺序是“6 1 5 9 4 7 2 8 3”！

既然现在已经搞清楚了解密法则，我们尝试一下去编程，首先需要一个数组来存储这一串数即int q[101] ， 并初始化这个数组即int q[101]=0,6,3,1,7,5,8,9,2,4。接下来就是模拟解密的过程了。
解密的第一步是将第一个数删除，最简单的方法是将所有后面的数都往前面挪动一位，将前面的数覆盖。就好比我们在排队买票，最前面的人买好离开了，后面所有的人就需要全部向前面走一步，补上之前的空位。
在这里， 我将引入两个整型变量head和tail。head用来记录队列的队首(即第一位) ，tail用来记录队列的队尾(即最后一位) 的下一个位置。

为什么tail不直接记录队尾，却要记录队尾的下一个位置呢？

这是因为当队列中只剩下一个元素时，队首和队尾重合会带来一些麻烦。我们这里规定队首和队尾重合时，队列为空。
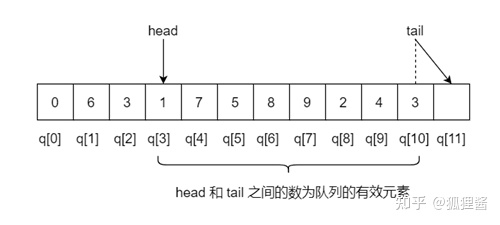
现在有9个数， 9个数全部放入队列之后head=1， tail=10， 此时head和tail之间的数就是目前队列中“有效”的数。如果要删除一个数的话， 就将head++就OK了， 这样仍然可以
保持head和tail之间的数为目前队列中“有效”的数。这样做虽然浪费了一个空间， 却节省了大量的时间， 这是非常划算的。新增加一个数也很简单， 把需要增加的数放到队尾即q[tail]之后再tail++就OK啦。

我们来小结一下， 在队首删除一个数的操作是head++； 。

在队尾增加一个数(假设这个数是x) 的操作是q[tail] = x ; tail ++ ;

请移步到该网站的算法基础课程中，《队列》的小节，习题在内容最后。

1024乐学编程-算法基础

我们这次先讲到这里，您可以进入上面的地址免费学习完整的算法课程。