无损卡尔曼滤波UKF与多传感器融合

Posted 2023-02-21 Young_Gy

非线性系统状态估计是一大难点。KF（Kalman Filter）只适用于线性系统。EKF（Extended Kalman Filter）利用泰勒展开将非线性系统线性化。可是，EKF在强非线性系统下的误差很大。本文将介绍一种新型的滤波算法UKF（Unscented Kalman Filter），其计算精度相比EKF更高并省略了Jacobian矩阵的计算。

Why UKF

本博客在之前两篇介绍了KF和EKF。那么，为什么还需要UKF呢，原因见下表：

模型	缺点	UKF对缺点改进
KF	只适用于线性系统	适用于非线性系统
EKF	线性化忽略了高阶项导致强非线性系统误差大；线性化处理需要计算Jacobian矩阵	对非线性的概率分布近似，没有线性化忽略高阶项； 不需要计算Jacobian矩阵

UKF简述

原理概述

首先，回顾下UKF需要解决的问题，已知系统的状态及其方差$x_k,P_k$。如果经过非线性函数$x_k+1 = f(x_k)$后，新的状态和方差如何求解。

EKF提供的方法是将非线性函数$f(x)$作泰勒一阶展开，利用Jacobian矩阵$H_j$近似将$f(x)$线性化为$H_j x$。这种方法一方面在强非线性系统下误差大，另一方面Jacobian矩阵的计算着实令人头疼。

UKF认为每一个状态$x_k,P_k$都可以用几个Sigma点（关键点）$X_sig$表示。当作用于非线性函数$f(x)$时，只需要将Sigma点$X_sig$作用于非线性函数$f(x)$得到$f(X_sig)$即可。通过得到的$f(X_sig)$可以计算新的状态$x_k+1,P_k+1$。

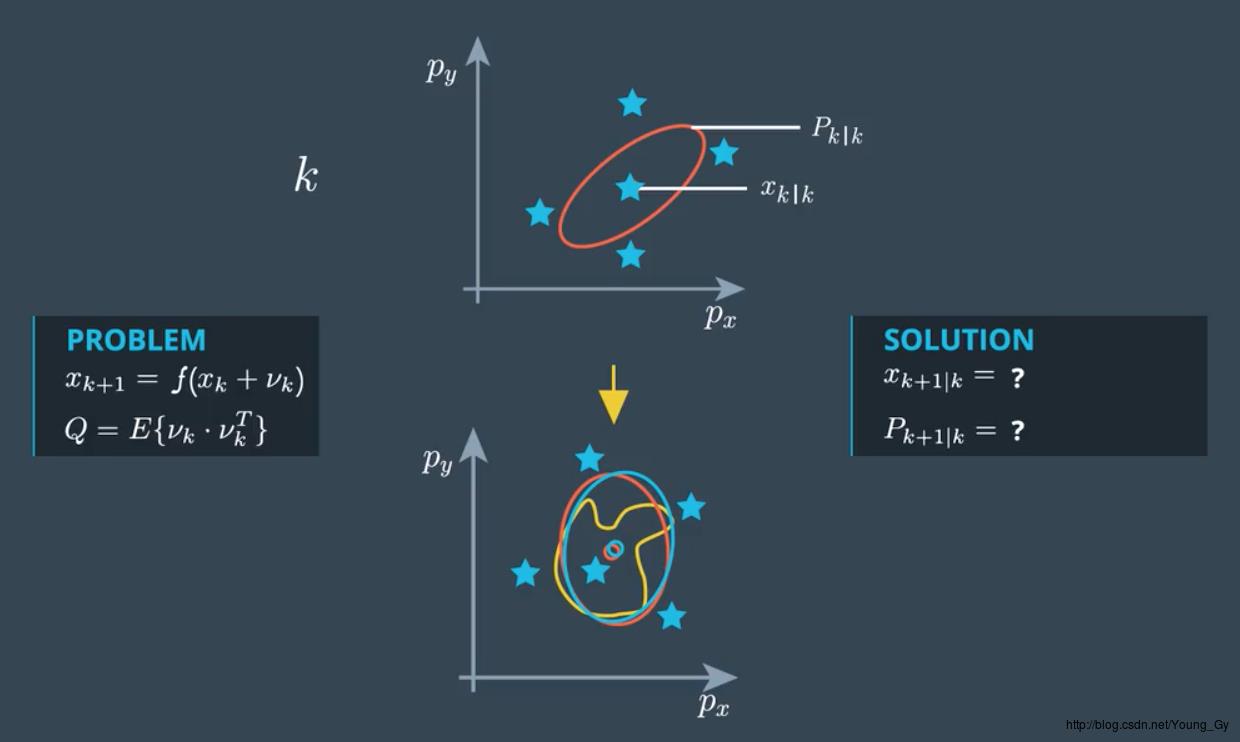
通过上面的介绍，我们知道UKF只是将非线性函数映射通过关键点映射来实现，那么出现几个问题：

1. 关键点怎么找
2. 找到关键点后如何求出新的状态$x_k+1,P_k+1$

关键点怎么找

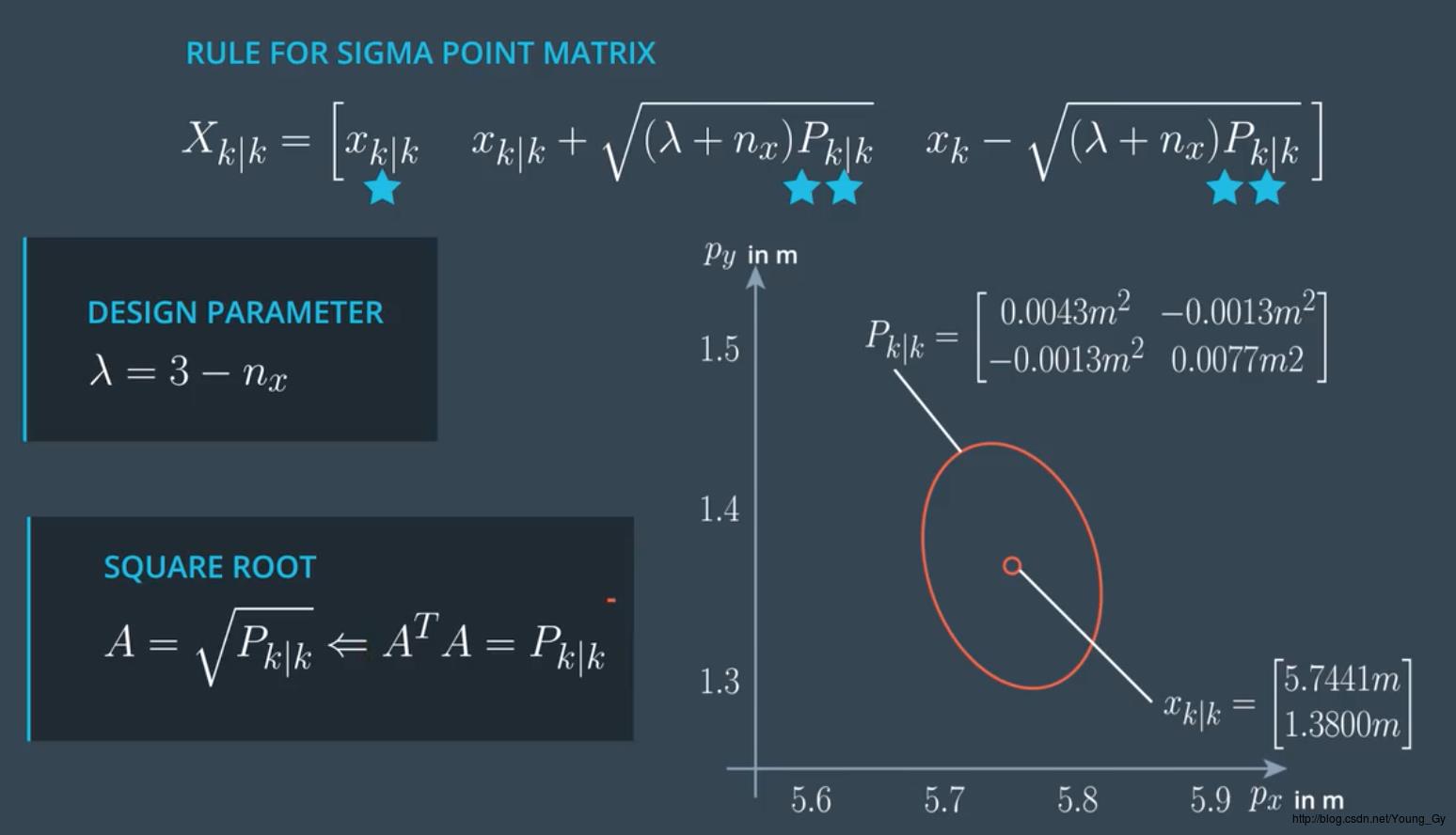
关键点的意义在于能够充分刻画原状态的分布情况，其经验公式如下图所示，需要注意的是：

• $n_x$代表$x_k|k$的大小
• $\\lambda$代表关键点的散开情况，一般采用经验值$\\lambda=3-n_x$

找到关键点后如何求出新的状态

新状态的求解公式如下图所示，需要注意的是：

• $X_k+1|k$代表Sigma点集合，$X_k+1|k,i$代表Sigma点集合中的第$i$个点
• $n_a$代表$x_k+1|k$增广后的大小
• $n_\\sigma$代表Sigma点集合的大小，一般$n_\\sigma = 1+2n_a$
• 权重$w_i$在$i==0$时$w_0=\\frac\\lambda\\lambda+n_a$，在$i!=0$时 w0=1UKF

  卡尔曼滤波器 - 两个相等传感器的融合

  扩展卡尔曼滤波EKF与多传感器融合

  扩展卡尔曼滤波EKF与多传感器融合

  无迹卡尔曼滤波UKF—目标跟踪中的应用(算法部分)

  在传感器融合的情况下使用哪种滤波器？