LeetCode

Posted 2021-02-04 tu9oh0st

前言

为了不让自己做公司笔试题时做不出来，所以刷题，挑了个好的刷题平台LeetCode

所以记录和分享自己的刷题思路和题解写了这个专栏。

最大子序和

题目描述

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

分析

最大子序列是要找出由数组成的一维数组中和最大的连续子序列。比如{5,-3,4,2}的最大子序列就是 {5,-3,4,2}，它的和是8,达到最大；而 {5,-6,4,2}的最大子序列是{4,2}，它的和是6。你已经看出来了，找最大子序列的方法很简单，只要前i项的和还没有小于0那么子序列就一直向后扩展，否则丢弃之前的子序列开始新的子序列，同时我们要记下各个子序列的和，最后找到和最大的子序列。
动态方程：
最大子序列和是连续的子序列
ThisSum[i]表示第i处，以A[i]结尾的子序列的最大和。
则状态方程为ThisSum[i]=max(ThisSum[i-1]+nums[i],nums[i])
也即是说，如果ThisSum[i-1]<0则ThisSum[i]就是nums[i],否则ThisSum[i]=nums[i]+ThisSum[i-1]（因为是以i结尾的

代码

package leetcode;

public class maxSubArray {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] nums = {-2,1,-3,4,-1,2,1,-5,4};
        System.out.println(maxSubArray(nums));
    }
    public static int maxSubArray(int[] nums) {
        int r,l;
        int maxSum = nums[0],thisSum = nums[0];
        int new_l = 0;
        for(int i = 1; i < nums.length; i++) {
            if(thisSum < 0) {
                thisSum = nums[i];
                new_l = i;
            }else {
                thisSum += nums[i];
            }
            if(thisSum > maxSum) {
                maxSum = thisSum;
                l = new_l;
                r = i;
            }
        }
        
        return maxSum;
    }
}

加一

题目描述

给定一个非负整数组成的非空数组，在该数的基础上加一，返回一个新的数组。

最高位数字存放在数组的首位， 数组中每个元素只存储一个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例?1:

输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。

示例?2:

输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。

分析

这题，一开始以为是给最后一个数+1，没想到是进位的问题，题目理解真是一知半解。。。语文还是要好好学的啊。

下面这个是我在百度中了解的：

将一个数字的每个位上的数字分别存到一个一维向量中，最高位在最开头，我们需要给这个数字加一，即在末尾数字加一，如果末尾数字是9，那么则会有进位问题，而如果前面位上的数字仍为9，则需要继续向前进位。

具体算法如下：首先判断最后一位是否为9，若不是，直接加一返回，若是，则该位赋0，再继续查前一位，同样的方法，知道查完第一位。如果第一位原本为9，加一后会产生新的一位，那么最后要做的是，查运算完的第一位是否为0，如果是，则在最前头加一个1。

贴出来代码

class Solution {
    public int[] plusOne(int[] digits) {
        int n = digits.length;
        for(int i = digits.length -1; i>=0;--i) {
            if(digits[i]<9) {
                ++digits[i];
                return digits;
            }
            digits[i] =0;
        }
        int[] res = new int[n+1];
        res[0] =1;
        return res;
    }
}

合并两个有序数组

题目描述

给定两个有序整数数组 nums1 和 nums2，将 nums2 合并到 nums1 中，使得 num1 成为一个有序数组。

说明:

• 初始化 nums1 和 nums2 的元素数量分别为 m 和 n。
• 你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。

示例:

输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6],       n = 3

输出: [1,2,2,3,5,6]

分析

思路1：

先合并两个数组，再来排序

思路2：

从后往前填充即可

先当两个数组都有元素的时候填充大的到末尾，如果有一个数组的数用完了，说明剩下的那个数组的所有数都小于当前填充的位置：
如果是第一个数组用完了，说明剩下的(最小的那些)全是数组2，把数组2填充进去就好了
如果是第二个数组用完了，说明剩下的全是数组1，不用填充了，他们已经在了

贴出来代码

public class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i = m - 1, j = n - 1, writeIdx = m + n - 1;
        while (i >= 0 && j >= 0)
            nums1[writeIdx--] = nums1[i] > nums2[j]? nums1[i--] : nums2[j--];
        while (j >= 0)
            nums1[writeIdx--] = nums2[j--];
    }
}

买卖股票的最佳时机II

题目描述

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

分析

1. 始终保存最小的买入价格
2. 始终保存最大的利润

比如数据2,7,1,3

首先找到最小买入是2，然后做差7-2=5，保存利润，然后到最小买入变成1，此时利润还是5，然后到3，注意，这里就是核心了。

如果1后面出现的数字足够大，大到和1做差的值大于5，那么最大利润值就改变，否则，最大利润还是5.

这里暗含的逻辑是，后面的数如果减1的差肯定比减2的差来的大。

贴出代码

class Solution {
public int maxProfit(int[] prices) {
       if (prices == null || prices.length == 0) {
           return 0;
       }
       int profit = 0;
       for (int i = 1; i < prices.length; i++) {
           if (prices[i - 1] < prices[i]) {
               profit += prices[i] - prices[i - 1];
           }
       }
       return profit;
   }
};

买卖股票的最佳时机

题目描述

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

分析

1. 始终保存最小的买入价格
2. 始终保存最大的利润

比如数据2,7,1，3

首先找到最小买入是2，然后做差7-2=5，保存利润，然后到最小买入变成1，此时利润还是5，然后到3，注意，这里就是核心了。

如果1后面出现的数字足够大，大到和1做差的值大于5，那么最大利润值就改变，否则，最大利润还是5.

这里暗含的逻辑是，后面的数如果减1的差肯定比减2的差来的大。

贴出代码

class Solution {
    public int maxProfit(int[] prices) {
        int result =0;
        int buy = Integer.MAX_VALUE;
        for(int price : prices){
            buy = min(buy,price);
            result = max(result,price - buy);
        }
        return result;
    }
    public int max(int i,int j){
        return i>j?i:j;
    }
    public int min(int i,int j){
        return i<j?i:j;
    }
}

转置矩阵

题目描述

给定一个矩阵 A， 返回 A 的转置矩阵。

矩阵的转置是指将矩阵的主对角线翻转，交换矩阵的行索引与列索引。

示例 1：

输入：[[1,2,3],[4,5,6],[7,8,9]]
输出：[[1,4,7],[2,5,8],[3,6,9]]

示例 2：

输入：[[1,2,3],[4,5,6]]
输出：[[1,4],[2,5],[3,6]]

分析

设数组中元素坐标位(x,y)，互换x,y位置即可

(x,y) --> (y,x)

所以重新设一个二维数组B

使得B.x=A[0].length

B.y=A.length

贴出代码

class Solution {
    public int[][] transpose(int[][] A) {
        int m = A.length;
        int n = A[0].length;
        int[][] B = new int[n][m];
        for(int i =0;i<n;i++) {
            for(int j = 0;j<m;j++) {
                B[i][j] =A[j][i];
            }
        }
        return B;
    }
}

求众数

题目描述

给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 ? n/2 ? 的元素。

你可以假设数组是非空的，并且给定的数组总是存在众数。

示例 1:

输入: [3,2,3]
输出: 3

示例?2:

输入: [2,2,1,1,1,2,2]
输出: 2

分析

众数的定义，题目已经给出，要解决的问题是，如何让计算机知道数组中相同元素出现的次数。

思路一：

众数出现次数大于n/2，然后对数组排序，取中间的元素

思路二（百度得来）：

利用哈希表的映射，储存数组中的数字以及它们出现的次数，当众数出现时，返回这个数字。

根据思路一，先对数组排序，然后取中间元素，结果超时，虽然答案对了，但是时间超过，这也不符合。

贴出来代码

//思路二
class Solution {
    public int majorityElement(int[] nums) {
               
        Map<Integer,Integer> map = new HashMap<Integer,Integer>(); 
        int n = nums.length;
        
        for(int num : nums)   //统计每个元素出现的次数
        {
            Integer count = map.get(num);
            if(count == null) 
                count =1;
            else
                count++;
            map.put(num,count);
            
            if(map.get(num) > n/2)
                return num;
        }
        
        return 0;
    }
}

两数之和 II - 输入有序数组

题目描述

给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。

函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

说明:

• 返回的下标值（index1 和 index2）不是从零开始的。
• 你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

示例:

输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

分析

设置两套循环，j=i+1; 判断条件：numbers[i]+numbers[j] = target才算成功。

贴出代码

class Solution {
    public int[] twoSum(int[] numbers, int target) {
         int[] index = new int[2];
        for(int i =0 ;i<numbers.length;i++){
            for(int j = i+1;j<numbers.length;j++){
                //System.out.println(index[0]+" "+index[1]);
                if(numbers[i]+numbers[j]==target){
                        index[0] = i +1;
                        index[1] = j+1;
                        break;
                }
            }
        }
        //System.out.println(index[0]);
        //System.out.println(index[1]);
        return index;
    }
}

杨辉三角

题目描述

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

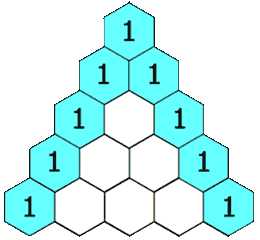
在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

分析

根据上面那个图，我们可以发现，第一行和第二行都由1组成。其他行的起始和结束都是1.内容由上一行相邻两个数组和组成。由此我们可以写出代码。

贴出代码

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        
        if(numRows == 0) 
            return res;
        
        for(int j = 0;j<numRows;j++) {
            List<Integer> row = new ArrayList<Integer>();
            row.add(1);
            
        for(int i = 1;i<j;i++) {
            List<Integer> prevRow = res.get(j-1);
            int temp = prevRow.get(i-1)+prevRow.get(i);
            row.add(temp);
        }
        
        if(j!=0)
            row.add(1);
        res.add(row);
        }
        return res;
    }
}

杨辉三角 II

题目描述

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

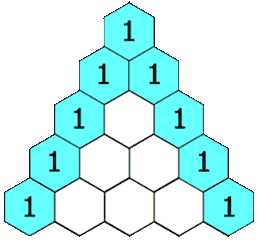
在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 3
输出: [1,3,3,1]

贴出代码

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> list = new ArrayList<>();
        if(rowIndex < 0)
            return list;
        list.add(1);
        if(rowIndex == 0)
            return list;
        for(int i = 1;i<=rowIndex;i++) {
            for(int j = list.size()-1;j>0;j--) {
                list.set(j, list.get(j-1)+list.get(j));
            }
            list.add(1);
        }
        return list;
    }
}

旋转数组

题目描述

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

示例 1:

输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释: 
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]

说明:

• 尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
• 要求使用空间复杂度为 O(1) 的原地算法。

分析

按照题目说明，要求空间复杂度为O(1)，并且这题有三种以上的解法。

1. 让数组插入到第一个数组之前。但这样空间复杂度就不是O(1)了。

这是错误的，超时了。不过能够得到正确答案。

class Solution {
    public void rotate(int[] nums, int k) {
      int n = nums.length;
        while(k != 0){
            int temp = nums[n-1];
            nums[n-1] = 0;
            for(int i = n-2; i > -1 ; i--) {
                int temp1 = nums[i];
                nums[i+1] = temp1;
                nums[i] = 0;
            }
            nums[0] = temp;
            k--;
        }
    }
}

解法1

借助O(n)的空间解法。再利用(i + k) % n = 旋转后的位置，可以将原有数组中的数据复制到新数组中。

例如：

3元素在数组中的2位置上，(2+3) % 7 = 5
5元素在数组中的4位置上，(4+3) % 7 = 0
6元素在数组中的5位置上，(5+3) % 7 = 1
7元素在数组中的6位置上，(6+3) % 7 = 2

根据以上可以推断出，诸如将一个数组向右偏移或者旋转多少步等之类的题目，可以通过(元素位置+偏移或旋转步数) 模与 数组长度可以得到偏移或者旋转之后的元素位置。

这是代码最少的方法了，不过因为leetcode对函数的类型是void，没有返回值，符合题目要求，不符合oj运行。

public int[] rotate(int[] nums, int k) {

    k =  k % nums.length;

    int[] result = new int[nums.length];

    for (int i = 0; i < nums.length; i++) {
        result[(i + k) % nums.length] = nums[i];
    }

    return result;
}

解法2

依旧可以利用(i+k)%n等于新i的思路，不过这次是每次调换一个元素，后一个元素的调换基于上一个的位置。

例如：让数组[1,2,3,4,5,6,7]向右旋转1，可以按照以下步骤来：

public void rotate2(int[] nums, int k) {
    if (nums.length == 0 || (k %= nums.length) == 0) {
        return;
    }
    int length = nums.length;
    int start = 0;
    int i = 0;
    int cur = nums[i];
    int cnt = 0;

    while (cnt++ < length) {
        i = (i + k) % length;
        int t = nums[i];
        nums[i] = cur;
        if (i == start) {
            ++start;
            ++i;
            cur = nums[i];
        } else {
            cur = t;
        }
    }
}

存在重复元素

题目描述

给定一个整数数组，判断是否存在重复元素。

如果任何值在数组中出现至少两次，函数返回 true。如果数组中每个元素都不相同，则返回 false。

示例 1:

输入: [1,2,3,1]
输出: true

示例 2:

输入: [1,2,3,4]
输出: false

示例 3:

输入: [1,1,1,3,3,4,3,2,4,2]
输出: true

分析

这是一道很简单的题，只需要遍历数组就可以，而且不用全部依次遍历，简单点的方法就是先对数组排完序，然后依次对比是否相等。

贴出代码

class Solution {
    public boolean containsDuplicate(int[] nums) {
        Arrays.sort(nums);
        for(int i = 0; i < nums.length-1; i++) {
            if(nums[i] == nums[i+1]) {
                return true;
            }
        }
        return false;
    }
}

存在重复元素 II

题目描述

给定一个整数数组和一个整数 k，判断数组中是否存在两个不同的索引 i 和 j，使得 nums [i] = nums [j]，并且 i 和 j 的差的绝对值最大为 k。

示例 1:

输入: nums = [1,2,3,1], k = 3
输出: true

示例 2:

输入: nums = [1,0,1,1], k = 1
输出: true

示例 3:

输入: nums = [1,2,3,1,2,3], k = 2
输出: false

分析

利用HashMap数据结构，每次存入数值钱先看一下有没有这个数了，如果已经有了，那么看一下这两个数的索引下标之差是不是小于等于k的，如果是的话那么久说明找到了，返回true，如果没有找到就返回false。

贴出代码

class Solution {
    public boolean containsNearbyDuplicate(int[] nums, int k) {
        HashMap<Integer,Integer> hm = new HashMap<>();
        for(int i = 0; i < nums.length; i++) {
            if(hm.containsKey(nums[i])) {
                int sub = i - hm.get(nums[i]);
                if(sub <= k) 
                    return true;
                else 
                    hm.put(nums[i], i);
        
            }else 
                hm.put(nums[i], i);
        
        }
            return false;
    }   
}

缺失数字

题目描述

给定一个包含 0, 1, 2, ..., n 中 n 个数的序列，找出 0 .. n 中没有出现在序列中的那个数。

示例 1:

输入: [3,0,1]
输出: 2

示例 2:

输入: [9,6,4,2,3,5,7,0,1]
输出: 8

说明:
你的算法应具有线性时间复杂度。你能否仅使用额外常数空间来实现?

分析

我们就简单把这道题当成一道数学题来算就可以了，因为是连续的，所以不缺失数字时候的加和可以计算，缺失数字之后的加和遍历一遍也可以计算出来，二者相减不就是缺失的数字了。

贴出代码

class Solution {
    public int missingNumber(int[] nums) {
        int res = nums.length;
        for(int i = 0; i < nums.length; i++){
            res +=(i-nums[i]);
        }
        return res;
    }
}

移动零

题目描述

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

输入: [0,1,0,3,12]
输出: [1,3,12,0,0]

说明:

1. 必须在原数组上操作，不能拷贝额外的数组。
2. 尽量减少操作次数。

分析

使用使用两个索引lastIndex和curIndex，curIndex从后向前遍历直到其元素为0，然后根据lastIndex与curIndex之间的差值，将元素前移。

贴出代码

class Solution {
    public void moveZeroes(int[] nums) {
        int curIndex = nums.length - 1;
        int lastIndex = nums.length - 1;
        //int count = 0;
        
        while(curIndex >= 0) {
            if(nums[curIndex] == 0) {
                int count = lastIndex - curIndex;
                for(int i = 0;i < count; i++) {
                    nums[curIndex + i] = nums[curIndex + i + 1];
                }//元素往前移动
                nums[lastIndex] = 0;
                lastIndex--;
            }
            curIndex--;
        }
    }
}

第三大的数

题目描述

给定一个非空数组，返回此数组中第三大的数。如果不存在，则返回数组中最大的数。要求算法时间复杂度必须是O(n)。

示例 1:

输入: [3, 2, 1]

输出: 1

解释: 第三大的数是 1.

示例 2:

输入: [1, 2]

输出: 2

解释: 第三大的数不存在, 所以返回最大的数 2 .

示例 3:

输入: [2, 2, 3, 1]

输出: 1

解释: 注意，要求返回第三大的数，是指第三大且唯一出现的数。
存在两个值为2的数，它们都排第二。

分析

道题让我们求数组中第三大的数，如果不存在的话那么就返回最大的数，题目中说明了这里的第三大不能和第二大相同，必须是严格的小于，而并非小于等于。这道题并不是很难，如果知道怎么求第二大的数，那么求第三大的数的思路都是一样的。那么我们用三个变量first,
second, third来分别保存第一大，第二大，和第三大的数，然后我们遍历数组，如果遍历到的数字大于当前第一大的数first，那么三个变量各自错位赋值，如果当前数字大于second，小于first，那么就更新second和third，如果当前数字大于third，小于second，那就只更新third。重复元引发结果有差异，如何解决？——引进变量fi，每有重复元fi–，如果最后fi小于3，那么说明没有第三大的数。 但是出现一个新的问题，如果有一个元素为Integer.MIN_VALUE，那么方法仍旧会有错。解决思路是设置一个标志量，只在第一次出现这个Integer.MIN_VALUE时，不处理fi–，后面的照常。

贴出代码

class Solution {
    public int thirdMax(int[] nums) {
     if(nums == null || nums.length == 0)
            return -1;
        if(nums.length == 1) {
            return nums[0];
        }
        if(nums.length == 2) {
            return Math.max(nums[0], nums[1]);
        }
        int len = nums.length;
        int first = Integer.MIN_VALUE;
        int second = Integer.MIN_VALUE;
        int third = Integer.MIN_VALUE;
        boolean fi = false;
        for(int num : nums) {
            if(num == Integer.MIN_VALUE && !fi) {
                fi = true;
                continue;
            }
            if(num == first || num == second || num == third) {
                len --;
                continue;
            }
            if(num > first) {
                third = second;
                second = first;
                first = num;
                continue;
            }else if(num > second) {
                third = second;
                second = num;
                continue;
            }else if(num > third) {
                third = num;
            }
        }
        return len >= 3 ? third : first;
    }
}

找到所有数组中消失的数字

题目描述

给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组，数组中的元素一些出现了两次，另一些只出现一次。

找到所有在 [1, n] 范围之间没有出现在数组中的数字。

您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。

示例:

输入:
[4,3,2,7,8,2,3,1]

输出:
[5,6]

分析

题目要求额外空间且时间复杂度为O(n)。按近小到大的顺序排序，如果该数字和对应数字-1所在索引不同，则交换位置，交换完i--，继续判断交换完的数字，循环完成后判断数字是否和索引+1的值相等，不等则加入集合。

贴出代码

class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> a = new ArrayList<Integer>();
        int temp;
        for(int i = 0; i < nums.length; i++) {
            if(nums[i] != nums[nums[i] - 1]) {
                temp = nums[nums[i] - 1];
                nums[nums[i] - 1] = nums[i];
                nums[i] = temp;
                i--;
                
            }
        }
        for(int i = 0; i < nums.length; i++) {
            if(nums[i] != i+1) {
                a.add(i+1);
            }
        }
        return a;
    }
}

最大连续1的个数

题目描述

给定一个二进制数组， 计算其中最大连续1的个数。

示例 1:

输入: [1,1,0,1,1,1]
输出: 3
解释: 开头的两位和最后的三位都是连续1，所以最大连续1的个数是 3.

注意：

• 输入的数组只包含 0 和1。
• 输入数组的长度是正整数，且不超过 10,000。

分析

这道题让我们求最大连续1的个数，不是一道难题。我们可以遍历一遍数组，用一个计数器cnt来统计1的个数，方法是如果当前数字为0，那么cnt重置为0，如果不是0，cnt自增1，然后每次更新结果res即可。

贴出代码

class Solution {
    public int findMaxConsecutiveOnes(int[] nums) {
        int res = 0, cnt = 0;
        for(int num : nums) {
            cnt = (num == 0) ? 0 : cnt +1;
            res = Integer.max(res, cnt);
        }
        return res;
    }
}

数组拆分I

题目描述

给定长度为 2n 的数组, 你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), ..., (an, bn) ，使得从1 到 n 的 min(ai, bi) 总和最大。

示例 1:

输入: [1,4,3,2]

输出: 4
解释: n 等于 2, 最大总和为 4 = min(1, 2) + min(3, 4).

提示:

1. n 是正整数,范围在 [1, 10000].
2. 数组中的元素范围在 [-10000, 10000].

分析

先给数组排个序，然后依次加上两两中最小的一个。

贴出代码

class Solution {
    public int arrayPairSum(int[] nums) {
        if(nums.length == 2) 
            return Math.min(nums[0], nums[1]);
        int sub = 0;
        int n = nums.length / 2;
        Arrays.sort(nums);
        for(int i = 0; i < nums.length; i++) {
            sub += Math.min(nums[i], nums[i++]);
        }
        return sub;
    }
}

重塑矩阵

题目描述

在MATLAB中，有一个非常有用的函数 reshape，它可以将一个矩阵重塑为另一个大小不同的新矩阵，但保留其原始数据。

给出一个由二维数组表示的矩阵，以及两个正整数r和c，分别表示想要的重构的矩阵的行数和列数。

重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。

如果具有给定参数的reshape操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。

示例 1:

输入: 
nums = 
[[1,2],
 [3,4]]
r = 1, c = 4
输出: 
[[1,2,3,4]]
解释:
行遍历nums的结果是 [1,2,3,4]。新的矩阵是 1 * 4 矩阵, 用之前的元素值一行一行填充新矩阵。

示例 2:

输入: 
nums = 
[[1,2],
 [3,4]]
r = 2, c = 4
输出: 
[[1,2],
 [3,4]]
解释:
没有办法将 2 * 2 矩阵转化为 2 * 4 矩阵。 所以输出原矩阵。

注意：

1. 给定矩阵的宽和高范围在 [1, 100]。
2. 给定的 r 和 c 都是正数。

分析

对于这种二维数组大小重新非配的问题的关键就是对应位置的坐标转换，最直接的办法就是先把原数组拉直，变成一条直线，然后再组成新的数组。所以这道题我们先判断给定数组是否能重塑成给定的大小，就是看两者的元素总数是否相同，直接行数乘以列数即可，然后我们新建一个目标大小的数组，并开始遍历，对于每个位置，我们先转为拉直后的一维坐标，然后在算出在原数组中的对应位置赋值过来即可。

贴出代码

class Solution {
    public int[][] matrixReshape(int[][] nums, int r, int c) {
        int m = nums.length, n = nums[0].length;
        if (r * c != m * n) {
            return nums;
        }
        int[][] res;
        res = new int[r][c];
        for (int i = 0; i < r; ++i){
            for( int j = 0; j < c; ++j){
                int k = i * c + j;
                res[i][j] = nums[k / n][k % n];
            }
        }
        return res;
    }
}

最短无序连续子数组

题目描述

给定一个整数数组，你需要寻找一个连续的子数组，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

你找到的子数组应是最短的，请输出它的长度。

示例 1:

输入: [2, 6, 4, 8, 10, 9, 15]
输出: 5
解释: 你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

说明 :

1. 输入的数组长度范围在 [1, 10,000]。
2. 输入的数组可能包含重复元素 ，所以升序的意思是<=。

分析

这个题目我就比较偷懒了，直接排序然后找前后不一样的数的位置就行了

贴出代码

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int[] sortedArr = Arrays.copyOf(nums,nums.length);
        Arrays.sort(sortedArr);
        int i = 0,j = nums.length - 1;
        while(nums[i] == sortedArr[i] && i < j)
            i++;
        while(nums[j] == sortedArr[j] && i < j)
            j--;
        if(i == j)
            return 0;
        else
            return j - i + 1;
    }
}

数组的度

题目描述

给定一个非空且只包含非负数的整数数组 nums, 数组的度的定义是指数组里任一元素出现频数的最大值。

你的任务是找到与 nums 拥有相同大小的度的最短连续子数组，返回其长度。

示例 1:

输入: [1, 2, 2, 3, 1]
输出: 2
解释: 
输入数组的度是2，因为元素1和2的出现频数最大，均为2.
连续子数组里面拥有相同度的有如下所示:
[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]
最短连续子数组[2, 2]的长度为2，所以返回2.

示例 2:

输入: [1,2,2,3,1,4,2]
输出: 6

注意:

• nums.length 在1到50,000区间范围内。
• nums[i] 是一个在0到49,999范围内的整数。

分析

这个题目还是利用HashMap数据结构的题目。

第一步：

首先还是利用HashMap类来统计各个数字出现的次数，将数值和次数分别作为key和value存入HashMap。

第二步：

找到频率最大的那几个数值（可以是一个也可以是多个数值），然后每一个分别用双指针方法找到在数组中第一次和最后一次出现的位置，找到他们中距离最小的那个，返回这个距离。

贴出代码

class Solution {
    public int findShortestSubArray(int[] nums) {
                int maxCount = 1;
        ArrayList<Integer> arr = new ArrayList<>();
        HashMap<Integer,Integer> hm = new HashMap<>();
        for(int n:nums){
            if(hm.containsKey(n)){
                int temp = hm.get(n) + 1;
                hm.put(n, temp);
                if(maxCount < temp){
                    maxCount = temp;
                }
            }else{
                hm.put(n,1);
            }
        }
        Set<Integer> set = hm.keySet();
        int minDis = Integer.MAX_VALUE;
        for(int n:set){
            int temp = Integer.MAX_VALUE;
            if(hm.get(n) == maxCount){
                int i=0,j = nums.length-1;
                while(nums[i] != n && i<j)
                    i++;
                while(nums[j] != n && i<j)
                    j--;
                temp = j - i + 1;
            }
            minDis = Math.min(temp,minDis);
        }
        return minDis;
    }
}

托普利茨矩阵

题目描述

如果一个矩阵的每一方向由左上到右下的对角线上具有相同元素，那么这个矩阵是托普利茨矩阵。

给定一个 M x N 的矩阵，当且仅当它是托普利茨矩阵时返回 True。

示例 1:

输入: 
matrix = [
  [1,2,3,4],
  [5,1,2,3],
  [9,5,1,2]
]
输出: True
解释:
在上述矩阵中, 其对角线为:
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]"。
各条对角线上的所有元素均相同, 因此答案是True。

示例 2:

输入:
matrix = [
  [1,2],
  [2,2]
]
输出: False
解释: 
对角线"[1, 2]"上的元素不同。

说明:

1. matrix 是一个包含整数的二维数组。
2. matrix 的行数和列数均在 [1, 20]范围内。
3. matrix[i][j] 包含的整数在 [0, 99]范围内。

进阶:

1. 如果矩阵存储在磁盘上，并且磁盘内存是有限的，因此一次最多只能将一行矩阵加载到内存中，该怎么办？
2. 如果矩阵太大以至于只能一次将部分行加载到内存中，该怎么办？

分析

在(l - 1)*(n - 1)矩阵各元素进行判断即可，即matrix[i][j] != matrix[i+1][j+1]这个条件。

贴出代码

class Solution {
    public boolean isToeplitzMatrix(int[][] matrix) {
        int l = matrix.length,n = matrix[0].length;
        for(int i = 0; i < l - 1; i++){
            for(int j = 0; j < n - 1; j++){
                    if(matrix[i][j] != matrix[i+1][j+1]){
                        return false;
                    }
            }
        }
        return true;
    }
}

图片平滑器

题目描述

包含整数的二维矩阵 M 表示一个图片的灰度。你需要设计一个平滑器来让每一个单元的灰度成为平均灰度 (向下舍入) ，平均灰度的计算是周围的8个单元和它本身的值求平均，如果周围的单元格不足八个，则尽可能多的利用它们。

示例 1:

输入:
[[1,1,1],
 [1,0,1],
 [1,1,1]]
输出:
[[0, 0, 0],
 [0, 0, 0],
 [0, 0, 0]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0
对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0
对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0

注意:

1. 给定矩阵中的整数范围为 [0, 255]。
2. 矩阵的长和宽的范围均为 [1, 150]。

分析

就用常规方法做，新设一个 res[][] array，遍历M，对于每一个cell， 遍历以它为中心的3x3的cells，得到平均值，存入res。需要注意的就是，3x3的边界问题。

贴出代码

class Solution {
    public int[][] imageSmoother(int[][] M) {
        int rows = M.length;
            int cols = M[0].length;
            int[][] res = new int[rows][cols];

            for(int i = 0; i < rows; i++){
                for(int j = 0; j < cols; j++){
                    int sum = 0;
                    int count = 0;
                    for(int x = Math.max(0,i-1); x <= Math.min(rows - 1, i + 1);x++){
                        for(int y = Math.max(0, j-1); y <= Math.min(cols - 1, j + 1); y++){
                            sum += M[x][y];
                            count++;
                        }
                    }
                    res[i][j] = sum / count;
                }
            }
            return res;
    }
}

岛屿的最大面积

题目描述

给定一个包含了一些 0 和 1的非空二维数组 grid , 一个 岛屿 是由四个方向 (水平或垂直) 的 1 (代表土地) 构成的组合。你可以假设二维矩阵的四个边缘都被水包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为0。)

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是11，因为岛屿只能包含水平或垂直的四个方向的‘1’。

示例 2:

[[0,0,0,0,0,0,0,0]]

对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

分析

找到上下左右中，1最多的那块的数量。DFS（深度优先搜索）。

深度优先遍历图的方法是，从图中某顶点v出发：
（1）访问顶点v；
（2）依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；
（3）若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

贴出代码

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int max = 0;
        for(int i = 0; i < grid.length; i++){
            for(int j = 0; j < grid[0].length; j++){
                if(1 == grid[i][j]){
                    max = Integer.max(max,DfsApply(grid, i, j));
                }
            }
        }
        return max;
    }
    public int DfsApply(int[][] grid, int i, int j){
        if(i >= 0 && i < grid.length && j >= 0 && j < grid[0].length && grid[i][j] == 1)
        {
            grid[i][j] = 0;
            return 1 + DfsApply(grid,i+1,j)+DfsApply(grid,i-1,j)+DfsApply(grid,i,j+1)+DfsApply(grid,i,j-1);
        }
        else return 0;
    }
}

按奇偶校验排序数组

题目描述

给定一个非负整数数组 A，返回一个由 A 的所有偶数元素组成的数组，后面跟 A 的所有奇数元素。

你可以返回满足此条件的任何数组作为答案。

示例：

输入：[3,1,2,4]
输出：[2,4,3,1]
输出 [4,2,3,1]，[2,4,1,3] 和 [4,2,1,3] 也会被接受。

提示：

1. 1 <= A.length <= 5000
2. 0 <= A[i] <= 5000

分析

利用栈的特性，新的元素放在数组的最后面（即栈顶），不过Java中的栈类，跟这个题目要求的数组，我实在无解，这两个怎么转换。

贴出代码

class Solution {
    public int[] sortArrayByParity(int[] A) {
        List<Integer> res = new ArrayList();
        List<Integer> odd = new ArrayList();
        for(int i = 0; i < A.length; i++){
            if (A[i] % 2 == 0)
                res.add(A[i]);
            else
                odd.add(A[i]);
        }
        int resLen = res.size();
        int oddLen = odd.size();
        int[] out = new int[resLen + oddLen];
        for(int j = 0; j < resLen; j++)
            out[j] = res.get(j);
        for(int n = 0; n < oddLen; n++)
            out[n + resLen] = odd.get(n);
        return out;
    }
}

单调数列

题目描述

如果数组是单调递增或单调递减的，那么它是单调的。

如果对于所有 i <= j，A[i] <= A[j]，那么数组 A 是单调递增的。 如果对于所有 i <= j，A[i]> = A[j]，那么数组 A 是单调递减的。

当给定的数组 A 是单调数组时返回 true，否则返回 false。

示例 1：

输入：[1,2,2,3]
输出：true

示例 2：

输入：[6,5,4,4]
输出：true

示例 3：

输入：[1,3,2]
输出：false

示例 4：

输入：[1,2,4,5]
输出：true

示例 5：

输入：[1,1,1]
输出：true

提示：

1. 1 <= A.length <= 50000
2. -100000 <= A[i] <= 100000

分析

按照递增和递减分别写两个函数，放到目标函数中做判断。

贴出代码

class Solution {
    public boolean isMonotonic(int[] A) {
         if(upMonotonic(A)||downMontonic(A))
            return true;
        else if(A.length == 1)
            return true;
        else return false;
    }
    public boolean upMonotonic(int[] A){
        int a,b;
        boolean t = false;
        for(int i = 1; i < A.length; i++){
            a = A[i - 1];
            b = A[i];
            if(a <= b)
                t =true;
            else{
                t = false;
                break;
            }
        }
        return t;
    }

    public boolean downMontonic(int[] A){
        int a,b;
        boolean t = false;
        for(int i = 1; i < A.length; i++){
            a = A[i - 1];
            b = A[i];
            if(a >= b)
                t =true;
            else{
                t = false;
                break;
            }
        }
        return t;
    }
}

1比特与2比特字符

题目描述

有两种特殊字符。第一种字符可以用一比特0来表示。第二种字符可以用两比特(10 或 11)来表示。

现给一个由若干比特组成的字符串。问最后一个字符是否必定为一个一比特字符。给定的字符串总是由0结束。

示例 1:

输入: 
bits = [1, 0, 0]
输出: True
解释: 
唯一的编码方式是一个两比特字符和一个一比特字符。所以最后一个字符是一比特字符。

示例 2:

输入: 
bits = [1, 1, 1, 0]
输出: False
解释: 
唯一的编码方式是两比特字符和两比特字符。所以最后一个字符不是一比特字符。

注意:

• 1 <= len(bits) <= 1000.
• bits[i] 总是0 或 1.

分析

题目说，2比特为10或11，所以遇到1的时候跳两位，遇到0开头就是1比特，跳一位。

贴出代码

class Solution {
    public boolean isOneBitCharacter(int[] bits) {
        int i;
        for(i = 0; i < bits.length - 1;){
            if(bits[i] == 0){
                i++;
            }else
                i = i + 2;
        }
        return (i == bits.length - 1) ? true : false;
    }
}

子集

题目描述

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

分析

先对数组中的元素进行排序，然后再用递归分治法进行求解。

贴出代码

class Solution {
    private List<List<Integer>> res;
    private List<Integer> list;
    private int[] set;
    private int num;


    public List<List<Integer>> subsets(int[] nums){
        res = new LinkedList<>();

        if(nums != null){
            list = new ArrayList<>();
            quickSort(nums, 0, nums.length -1);
            set = nums;
            for(int i = 0; i <= nums.length; i++){
                num = i;
                subset(0);
            }
        }
        set = null;
        list = null;
        return res;
    }

    public void subset(int start){
        if(num == 0){
            List<Integer> tmp = new ArrayList<>();
            for(Integer i : list){
                tmp.add(i);
            }
            res.add(tmp);
            return;
        }
        int endFirst = set.length - num;
        for(int i = start; i <= endFirst; i++){
            list.add(set[i]);
            num--;
            subset(i + 1);
            num++;
            list.remove(new Integer(set[i]));
        }
    }
    private void quickSort(int[] arr, int lo,int hi){
        if(lo < hi){
            int mid = getMid(arr,lo,hi);
            quickSort(arr,lo,mid -1);
            quickSort(arr,mid + 1,hi);
        }
    }
    private int getMid(int[] arr,int lo,int hi){
        int tmp = arr[lo];
        while(lo < hi){
            while(lo < hi && arr[hi] > tmp){
                hi--;
            }
            arr[lo] = arr[hi];
            while(lo < hi && arr[lo] < tmp){
                lo++;
            }
            arr[hi] = arr[lo];
        }
        arr[lo] = tmp;
        return lo;
    }
}