描述
给定一个链表,旋转链表,将链表每个节点向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL
示例 2:
输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NULL
解法:双指针
思路
求解这道题等价于找到链表倒数第 k 个节点,然后将之前的所有节点放到链表的尾部,形成一个新的链表,相当于 LeetCode 第 19 题的进阶版。
对于寻找单向链表的倒数第 \\(k\\) 个元素问题,可以采用双指针的方法进行求解。
- 令指针
p1和指针p2均指向表头,然后让指针p2跳转 \\(k - 1\\) 次,此时指针p2处于链表的第 \\(k\\) 个节点
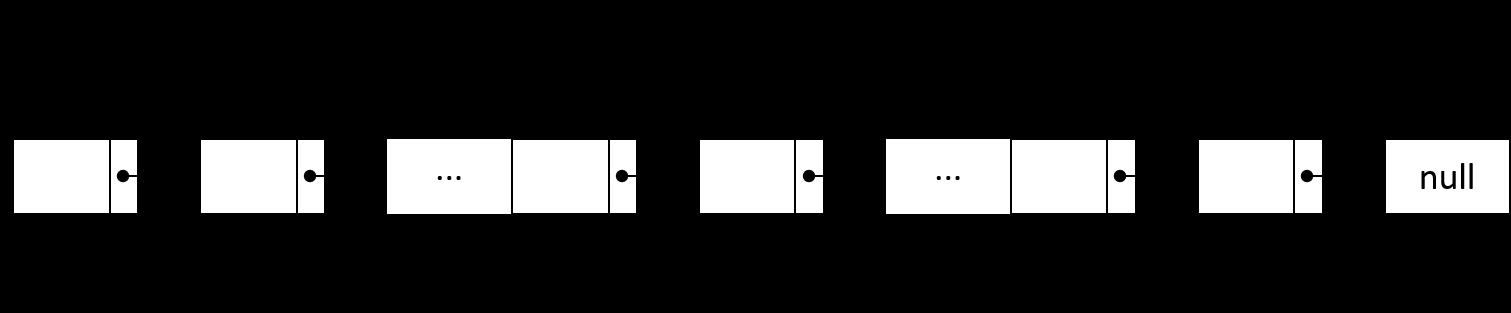
- 接着,让两个指针同时向链表尾部跳转,直到指针
p2处于链表的尾部,此时,指针p1指向的节点正是链表的倒数第 \\(k\\) 个节点
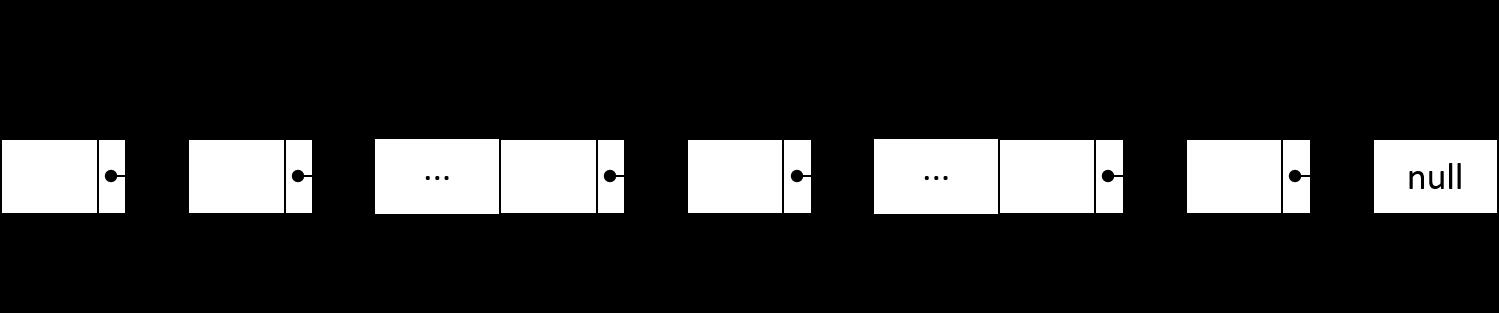
在找到倒数第 \\(k\\) 个节点后,只需要将指针 p2 指向链表头 head、指针 p1 的前一个节点的 next 指针指向 null,最后指针 p1 就是新的链表的表头。
值得注意的是,在这道题中,我们需要找到的是链表的倒数第 \\(k+1\\) 个节点,从而才能对该节点的 next 指针进行操作(指向 null)。同样地,也需要注意一些边界情况,比如表头 head 为空,k 大于链表长度等。
Java 实现
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode rotateRight(ListNode head, int k) {
// 边界情况处理
if (head == null) {
return head;
}
// 统计链表长度并对k进行取余操作
int length = 1;
ListNode tmp = head;
while (tmp.next != null) {
tmp = tmp.next;
++length;
}
k = k % length;
if (k == 0) {
return head;
}
// 寻找倒数第k+1个节点
ListNode p1 = head, p2 = head;
for (int i = 0; i < k; ++i) {
p2 = p2.next;
}
while (p2.next != null) {
p1 = p1.next;
p2 = p2.next;
}
// 旋转链表
ListNode newHead = p1.next;
p1.next = null;
p2.next = head;
return newHead;
}
}
// Runtime: 6 ms
// Your runtime beats 100.00 % of java submissions.
Python 实现
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def rotateRight(self, head, k):
"""
:type head: ListNode
:type k: int
:rtype: ListNode
"""
# 边界情况处理
if not head:
return head
# 统计链表的长度并对k进行取余操作
tmp, n = head, 1
while tmp.next:
tmp, n = tmp.next, n + 1
k = k % n
if k == 0:
return head
# 找到倒数第k+1个节点
p1, p2 = head, head
for i in range(k):
p2 = p2.next
while p2.next:
p1 = p1.next
p2 = p2.next
# 旋转链表
new_head = p1.next
p1.next, p2.next = None, head
return new_head
# Runtime: 44 ms
# Your runtime beats 99.11 % of python3 submissions.
复杂度分析
- 时间复杂度:\\(O(n)\\),其中 \\(n\\) 表示链表的长度。首先需要迭代 \\(n\\) 次找出链表的长度,接着让指针
p2迭代 \\(k\\) 次到达第 \\(k+1\\) 个节点的位置,最后还需要迭代 \\(n-(k+1)\\) 次使得两个指针一个指向链表尾部,一个指向倒数第 \\(k+1\\) 个节点,而迭代所执行的操作的时间复杂度都是 \\(O(1)\\) 的,所以最后总的时间复杂度是 \\(O(n)\\) 的 - 空间复杂度:\\(O(1)\\)