LeetCode动态规划Edit Distance

Posted 2021-01-13 华不摇曳

描述

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

1. Insert a character
2. Delete a character
3. Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace \'h\' with \'r\')
rorse -> rose (remove \'r\')
rose -> ros (remove \'e\')

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove \'t\')
inention -> enention (replace \'i\' with \'e\')
enention -> exention (replace \'n\' with \'x\')
exention -> exection (replace \'n\' with \'c\')
exection -> execution (insert \'u\')

 

思路：动态规划

这是一个经典的动态规划问题，思路参考斯坦福的课程：http://www.stanford.edu/class/cs124/lec/med.pdf

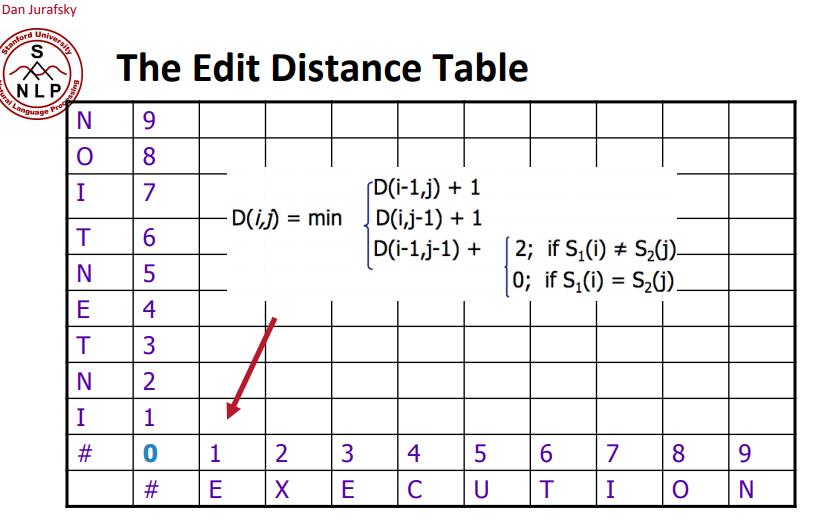
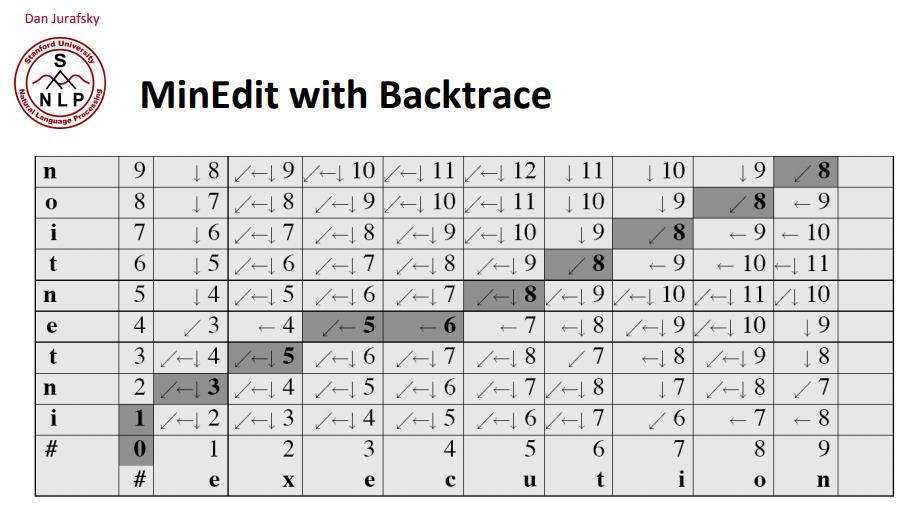
这里把加2变成加1即可

 

1. dp[i][0] = i;
2. dp[0][j] = j;
3. dp[i][j] = dp[i - 1][j - 1], if word1[i - 1] = word2[j - 1];
4. dp[i][j] = min(dp[i - 1][j - 1] + 1, dp[i - 1][j] + 1, dp[i][j - 1] + 1), otherwise.

 

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<vector<int> > dp(m+1, vector<int>(n+1, 0));
        for(int i = 1;i<=m;++i)
            dp[i][0] = i;
        for(int i = 1;i<=n;++i)
            dp[0][i] = i;
        for(int i = 1;i<=m;++i){
            for(int j = 1;j<=n;++j){
                if(word1[i-1] == word2[j-1])
                    dp[i][j] = dp[i-1][j-1];
                else
                    dp[i][j] = min(dp[i-1][j-1], min(dp[i][j-1], dp[i-1][j])) + 1;
            }
        }
        return dp[m][n];
    }
};