leetcode5. Longest Palindromic Substring

Posted 2021-01-08 yuchi328

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

Input: "cbbd"
Output: "bb"


注意不存在回文串的处理。此题还有DP和马拉车解法。

 1 class Solution {
 2 public:
 3     string longestPalindrome(string s) {
 4         int resNum = 0;
 5         string resStr = "";
 6         for(int i=0;i<s.size();i++){
 7             if(s[i] == s[i+1]&&i+1<s.size()){ //偶数
 8                 int j;
 9                 for(j=1;i-j>=0&&i+1+j<s.size();j++){
10                     if(s[i-j] != s[i+1+j]) break;
11                 }
12                 if(2*j>resNum) {
13                     resNum = 2*j;
14                     resStr = s.substr(i-j+1,2*j);
15                 }
16             }
17             if(s[i] == s[i+2]&&i+2<s.size()){ //奇数
18                 int j;
19                 for(j=1;i-j>=0&&i+2+j<s.size();j++){
20                     if(s[i-j] != s[i+2+j]) break;
21                 }
22                 if(2*j+1>resNum) {
23                     resNum = 2*j+1;
24                     resStr = s.substr(i-j+1,2*j+1);
25                 }
26             }
27         }
28         if(resStr == ""&&s.size()>0) resStr = s.substr(0,1);
29         return resStr;
30     }
31 };

 DP的做法，递推公式：

设dp[i][j]为i到j的子串是否为回文，则有

1.dp[i][j] = true （i == j）

2.dp[i][j] = s[i]==s[j] （i+1 == j）

3.dp[i][j] = s[i]==s[j]&&dp[i+1][j-1] (i+1<j)

注意遍历的顺序，依赖关系，可以从左向右，或者从上到下遍历。

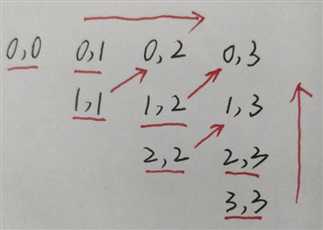
从左到右：

 1 class Solution {
 2 public:
 3     string longestPalindrome(string s) {
 4         int dp[1000+1][1000+1] = {0}, left = 0, right = 0, len = 0;
 5         for (int i = 0; i < s.size(); ++i) {
 6             for (int j = 0; j < i; ++j) {
 7                 if(j+1 == i) dp[j][i] = s[j]==s[i]?1:0;
 8                 else dp[j][i] = s[j]==s[i]&&dp[j+1][i-1]?1:0;
 9                 if(dp[j][i] && i-j+1>len){
10                     len = i-j+1;
11                     left = j;
12                     right = i;
13                 }
14             }
15             dp[i][i] = 1;
16         }
17         return s.substr(left, right - left + 1);
18     }
19 };

从上到下：

 1 class Solution {
 2 public:
 3     string longestPalindrome(string s) {
 4         int dp[1000+1][1000+1] = {0}, left = 0, right = 0, len = 0;
 5         for (int i = s.size()-1; i >= 0; i--) {
 6             for (int j = s.size()-1; j > i; j--) {
 7                 if(i+1 == j) dp[i][j] = s[j]==s[i]?1:0;
 8                 else dp[i][j] = s[j]==s[i]&&dp[i+1][j-1]?1:0;
 9                 if(dp[i][j] && j-i+1>len){
10                     len = j-i+1;
11                     left = i;
12                     right = j;
13                 }
14             }
15             dp[i][i] = 1;
16         }
17         return s.substr(left, right - left + 1);
18     }
19 };